2021年の第2問は、方程式からの出題でした。 正の整数m、nがあり、mを中央値とした連続する11個の整数(m−5,……,m,……,m+5)の和から18を引いた数と、nを中央値とした連続する9個の整数(n−4,……,n,……n+4)の和に9を加えた数が等しくなった。このときm+nの値として妥当なのはどれか。①13②14③15④16⑤17 連続するk個(ただしkは奇数)の数があって、その中央値がhのとき、この連続するk個の数の和はk×hになります。例をあげて説明すると、
では、本問の解説。 mを中央値とした連続する11個の整数の和は11mだから、「mを中央値とした連続する11個の整数の和から18を引いた数」は11m−18。 nを中央値とした連続する9個の整数の和は9nだから、「nを中央値とした連続する9個の整数の和に9を加えた数」は9n+9。 これらが等しいので、11m−18=9n+9。ここから先は、不定方程式ですね。
m+nの値は3つありますね。9+8=17。18+19=37。27+30=57。 本問には、「妥当なのはどれか」と書いてあるので、このうち選択肢にあるものを選べばよいのです。正解は、肢⑤です。

では、本問の解説。 mを中央値とした連続する11個の整数の和は11mだから、「mを中央値とした連続する11個の整数の和から18を引いた数」は11m−18。 nを中央値とした連続する9個の整数の和は9nだから、「nを中央値とした連続する9個の整数の和に9を加えた数」は9n+9。 これらが等しいので、11m−18=9n+9。ここから先は、不定方程式ですね。

m+nの値は3つありますね。9+8=17。18+19=37。27+30=57。 本問には、「妥当なのはどれか」と書いてあるので、このうち選択肢にあるものを選べばよいのです。正解は、肢⑤です。

















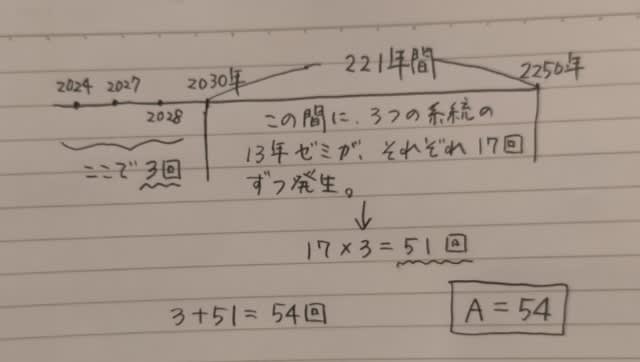


 次に、Aがどう答えたかと、その時Bはどう推論するかを整理します。
次に、Aがどう答えたかと、その時Bはどう推論するかを整理します。




 赤い三角形と青い三角形は、どちらも直角二等辺三角形(1:1:√2の三角定規)で、相似です。aとbの長さの比が2:1ということは、赤い三角形のそれぞれの長さを2 倍したものが青い三角形だということ。いま、AC=BC=kとすると、BE=DE=2kだから、EC=3k。
赤い三角形と青い三角形は、どちらも直角二等辺三角形(1:1:√2の三角定規)で、相似です。aとbの長さの比が2:1ということは、赤い三角形のそれぞれの長さを2 倍したものが青い三角形だということ。いま、AC=BC=kとすると、BE=DE=2kだから、EC=3k。


 さて、求めるものはaの長さですので、もう一度赤い三角形に戻る必要があります。
さて、求めるものはaの長さですので、もう一度赤い三角形に戻る必要があります。
