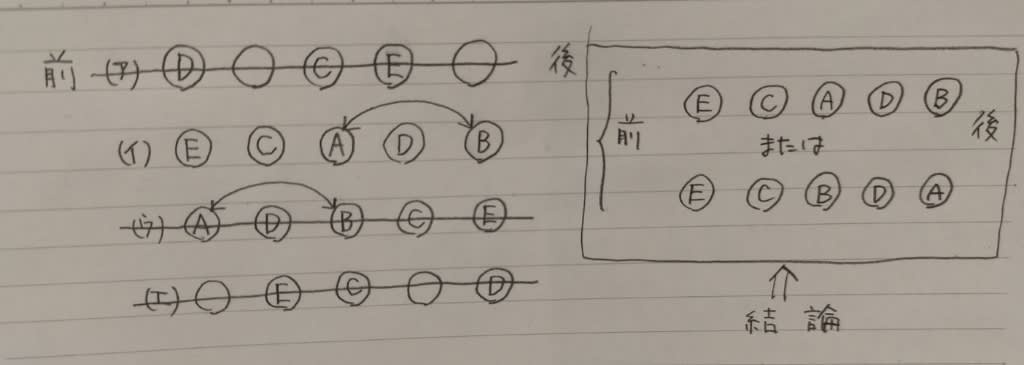
2021年出題。 A、B、C、D、Eの5人でプレゼントの交換を行った。 5人はそれぞれ1つずつプレゼントを持ち寄り、自分が持ってきたものをほかの人に渡したところ、5人全員にプレゼントが行き渡った。 これについて次のことがわかっているとき、正しいのはどれか。 ・Aにプレゼントをあげた人はDからプレゼントを貰った。 ・Bにプレゼントをあげた人はAからプレゼントを貰った。 ・Eはプレゼントをあげた人からプレゼントを貰った。 ➀AはCにプレゼントをあげた。 ➁BはDにプレゼントをあげた。 ③DはEにプレゼントをあげた。 ④Cにプレゼントをあげた人はBからプレゼントを貰った。 ⑤Dにプレゼントをあげた人はBからプレゼントを貰った。 はじめの条件は、D→◯→Aとします。(Aにプレゼントをあげた人を◯としました)。 次の条件は、A→△→B(Bにプレゼントをあげた人が△)。 最後の条件は、E⇄□(Eがプレゼントをあげた人が□)。 まとめると、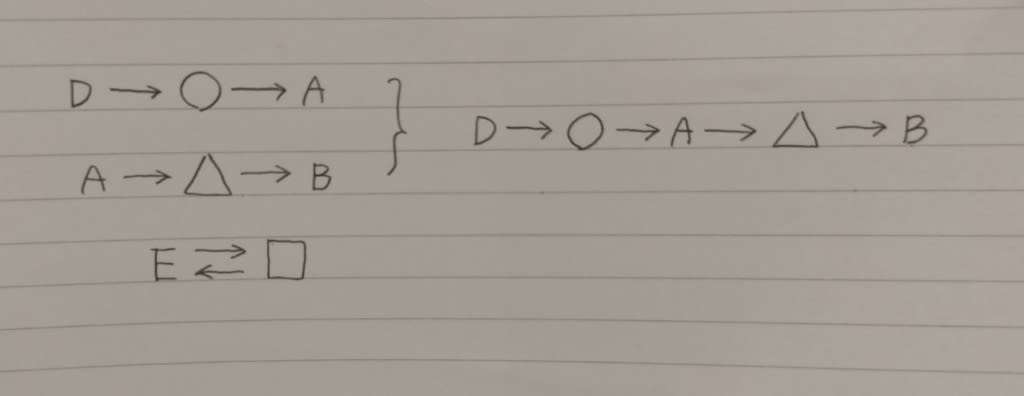
ポイントは、□は誰か?です。 □はAではありません。 □がAだとすると、◯はEになります。 とすると、Eは、Dからプレゼントを貰って、自分の持ってきたプレゼントをAに渡したことになるので、最後の条件を満たしません。 また、□はBでもありません。 □がBならば、△がEになる。 とすると、Eは、Aからプレゼントを貰って、自分が持ってきたプレゼントをBに渡したことになるからです。 また、□はDでもありません。 □がDならば、DはEにプレゼントをあげたのだから、◯がEになる。 ところがEはAに自分が持ってきたプレゼントを渡している。 これはやはり最後の条件を満たさない。 当然、□はEではない。 以上より、□は、Cしかないのです。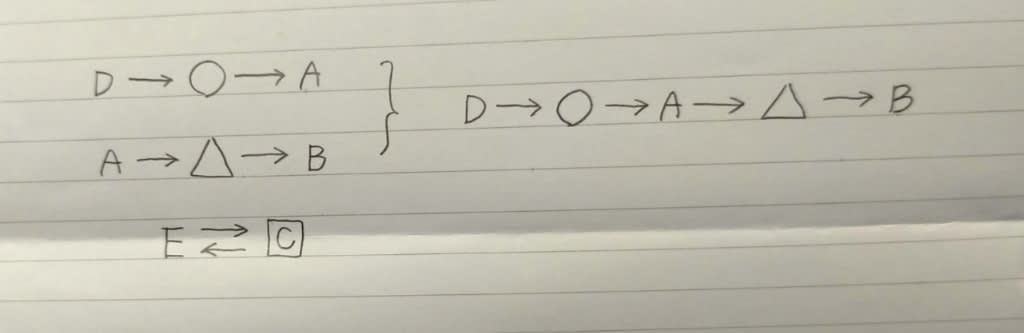
EとCはお互いにプレゼントを交換しましたが、もう一組プレゼントを交換した二人がいたならば、残る一人は、誰にもプレゼントを渡せないし、誰からもプレゼントを貰うことができません。 だから、残る三人は、こうなりますね。
ここに、A、B、Dが、入ります。 Dは、◯にプレゼントを渡し、◯はAにプレゼントを渡したので、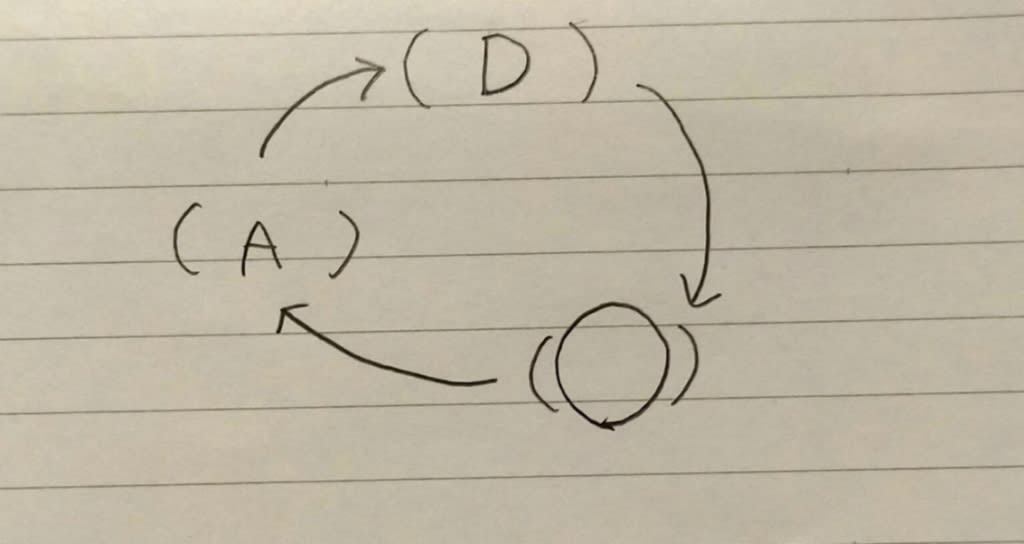
◯は残ったBしかない。
確かに、条件を満たしています(△はD)。結論、
正解は、肢⑤です。









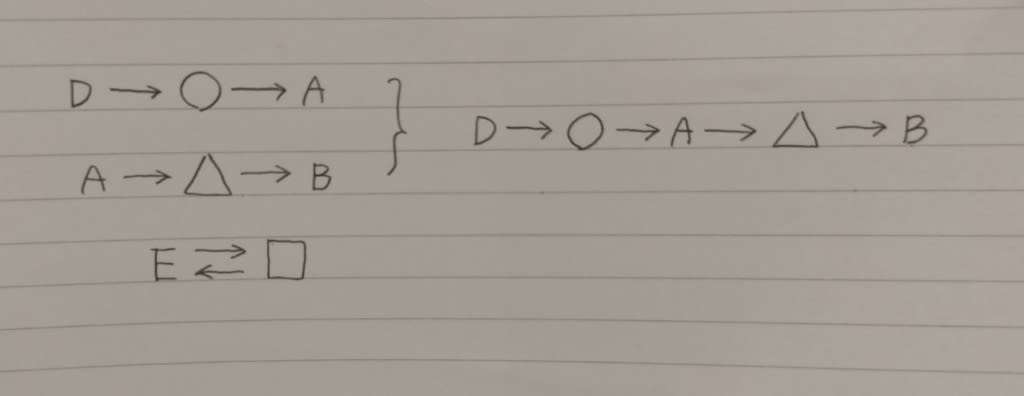
ポイントは、□は誰か?です。 □はAではありません。 □がAだとすると、◯はEになります。 とすると、Eは、Dからプレゼントを貰って、自分の持ってきたプレゼントをAに渡したことになるので、最後の条件を満たしません。 また、□はBでもありません。 □がBならば、△がEになる。 とすると、Eは、Aからプレゼントを貰って、自分が持ってきたプレゼントをBに渡したことになるからです。 また、□はDでもありません。 □がDならば、DはEにプレゼントをあげたのだから、◯がEになる。 ところがEはAに自分が持ってきたプレゼントを渡している。 これはやはり最後の条件を満たさない。 当然、□はEではない。 以上より、□は、Cしかないのです。
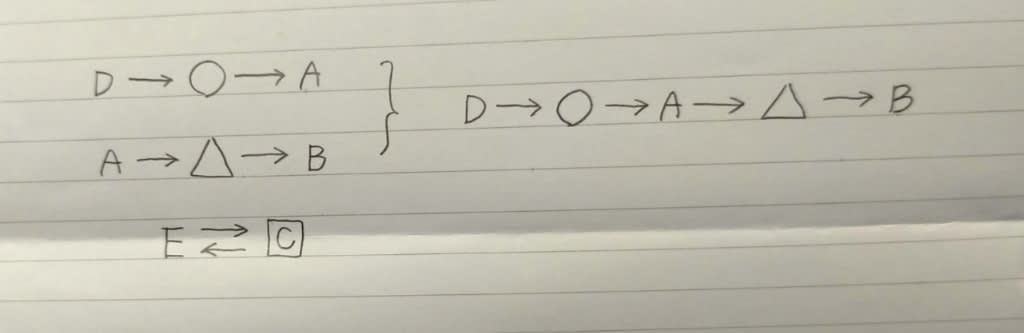
EとCはお互いにプレゼントを交換しましたが、もう一組プレゼントを交換した二人がいたならば、残る一人は、誰にもプレゼントを渡せないし、誰からもプレゼントを貰うことができません。 だから、残る三人は、こうなりますね。

ここに、A、B、Dが、入ります。 Dは、◯にプレゼントを渡し、◯はAにプレゼントを渡したので、

◯は残ったBしかない。

確かに、条件を満たしています(△はD)。結論、

正解は、肢⑤です。






















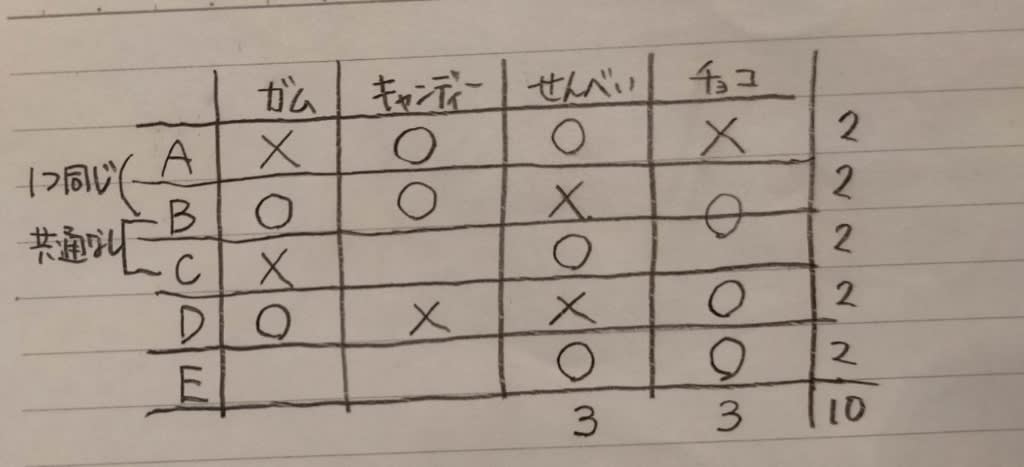
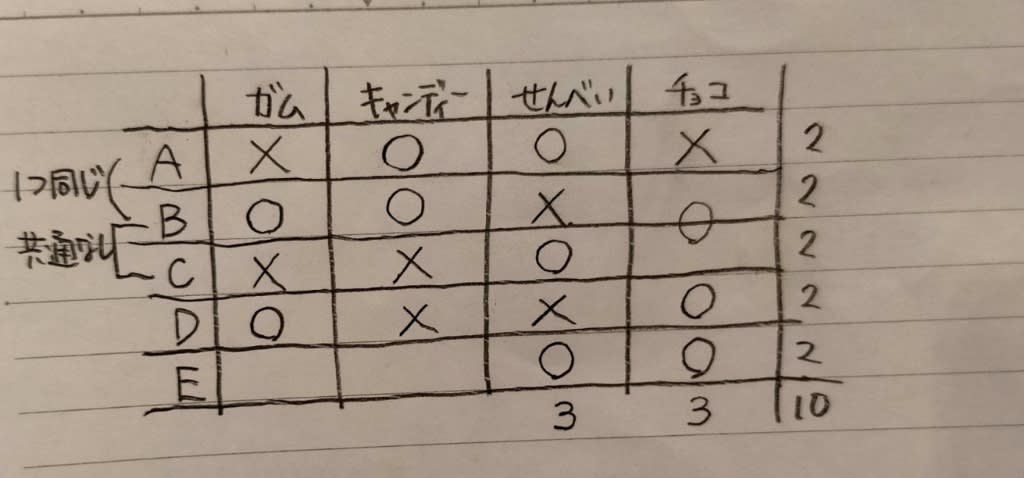
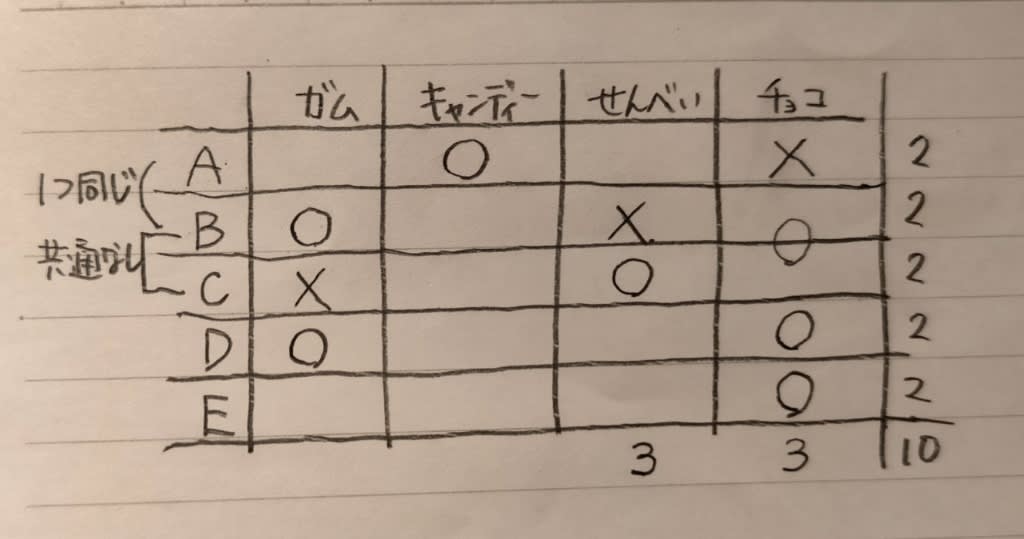 Dが選んだものはガムとチョコレートで、キャンディー、せんべいは選んでいません。
Dが選んだものはガムとチョコレートで、キャンディー、せんべいは選んでいません。 肢③はダメ。 せんべいを選んだ3人は、AとCとEですね。
肢③はダメ。 せんべいを選んだ3人は、AとCとEですね。
 肢➀もダメ。 AとBは、何か一種類同じお菓子を選んでいますが、それはキャンディーしかない。
肢➀もダメ。 AとBは、何か一種類同じお菓子を選んでいますが、それはキャンディーしかない。