折り曲げ。2019年度奈良県教員採用試験小学全科8

1辺が15cmの正方形ＡＢＣＤの紙を、図のように、頂点Ｃが辺ＡＤの中点Ｅと重なるように折り返した。このとき、線分ＡＦの長さとして正しいものを、下の1〜5から1つ選べ。
結論から言うと、ＡＦ＝15×2/3＝10cmで、正解は肢2です。　　　　　　　　　　　　　　　　　　これは、あまりにもよく出題される問題なので、公式として覚えておいても損にはなりません。　　　　　　　　　　　　　　　　　　正方形の紙(折り紙)があって、本問のように、1つの角が向かい合う辺の中点に来るように折り曲げると、必ずこうなります。
まずは、本問を、普通に解いてみると、
数学苦手な方は、これは辛いです。　　　　　　　　　　　　　　　　　　３平方の定理のところの計算も大変だし、相似な三角形も気が付きにくい。気が付いたとしても、比例の式が正しく立てられるか。　　　　　　　　　　　　　　　　　　さらに、本問はまだ楽な方で、もしもＦＨの長さや、ＢＨの長さを求めろなどと言われると、もう一つ、△ＧＦＨも相似であることを使わなければいけません。　　　　　　　　　　　　　　　　　　ここが本当にこわいところで、数学が得意な人は、「それがどうしたの?そうすればいいじゃん」ですし、苦手な人は、「気が狂いそう。この問題は二度とできない」なのです。　　　　　　　　　　　　　　　　　　数十年数学を人に教えてきた経験から分かります。だから、「三つ子のヒーロー」の公式を覚えておいたほうがいいと思うのです。なぜ3対5対16なのかというと、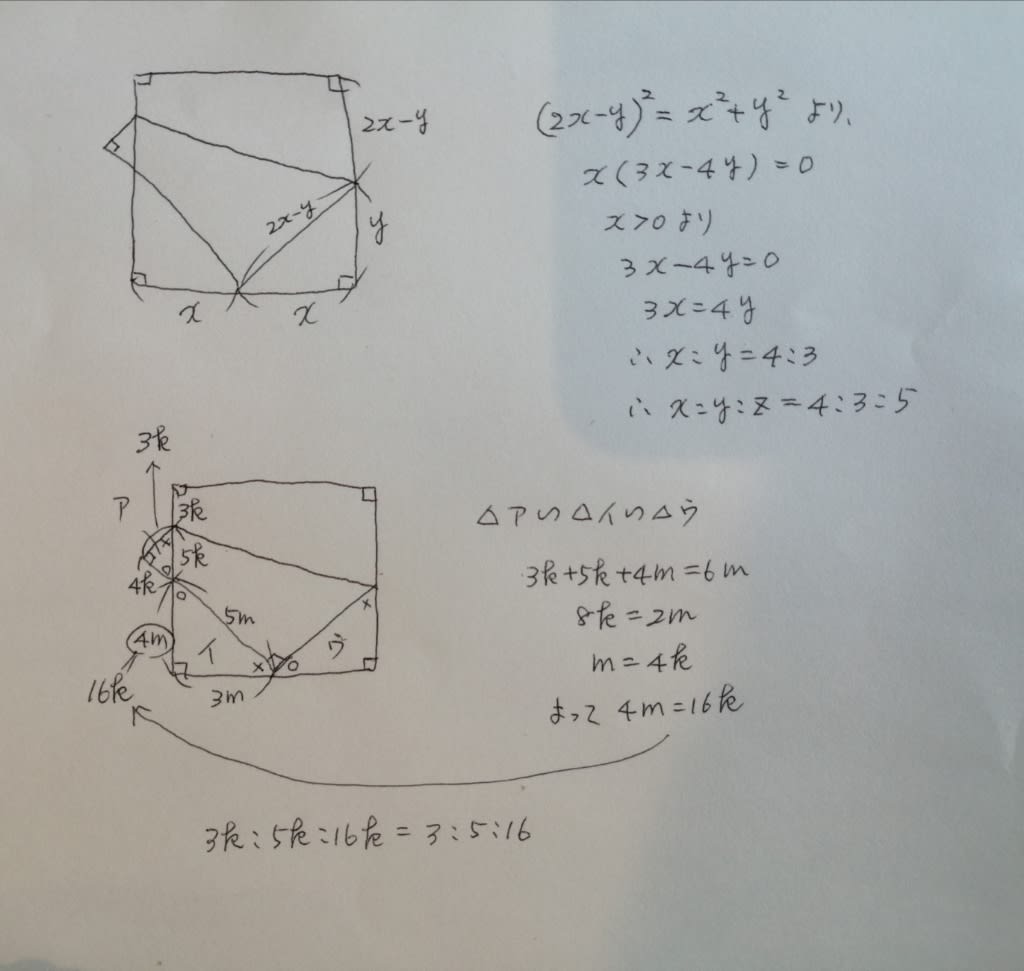
はじめに書いたように、本問は、結局のところ、ＡＦの長さは、ＡＢの長さの24分の16、つまり3分の2の長さになるので、10cmとなるのです。　　　　　　　　　　　　　　　　　　もう一つ、裏公式があるのですが、それは次に問題が出てきたらやりま〜す。ここをポチッとお願いします。→
にほんブログ村

相当算 平成30年度国家一般職（大卒）

箱の中に何本かの缶ジュースがあり、A～Eの5人で分けた。次のことが分かっているとき、DとEに分けられた缶ジュースの本数の合計は何本か。　　　　　　　　　　　　　　　　　　　　　◯AとBに分けられた缶ジュースの本数の合計は、分ける前の本数の7／18である。　　　　　　　　　　　　　　　　　　　　　◯AとCに分けられた缶ジュースの本数の合計は、分ける前の本数の4／9である。　　　　　　　　　　　　　　　　　　　　　◯BとCに分けられた缶ジュースの本数の合計は、分ける前の本数の1／3である。　　　　　　　　　　　　　　　　　　　　　◯Aが自分に分けられた缶ジュースをBに4本渡したところ、AとBの缶ジュースの本数は等しくなった。　　　　　　　　　　　　　　　　　　　　　①26本　②28本　③30本　④32本　⑤34本　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　「分ける前の缶ジュースの本数は100本だ」という人がいたら、その人は嘘つきです。　　　　　　　　　　　　　　　　　　　　なぜならば、100本の7／18などないからです。　　　　　　　　　　　　　　　　　　　　つまり、はじめの条件から、分ける前の本数は、18の倍数だと分かります。　　　　　　　　　　　　　　　　　　　　二つ目の条件からは、分ける前の本数が9の倍数だと分かり、三つ目の条件からは、分ける前の本数が3の倍数だと分かります。　　　　　　　　　　　　　　　　　　　　18と9と3の最小公倍数は18なので、分ける前の本数を18k本とします。すると、

ゆえに、

DとEの合計は、7.5の倍数なので、選択肢上、正解は③しかありません。　　　　　　　　　　　　　　　　　　　　　選択肢なしでやってみましょう。

ここで、最後の条件より、

ってな寸法です。　　　　　　　　　　　　　　　　　　　　　　　　　　　ここをポチッとお願いします。→"""



にほんブログ村"

2019年度京都市教員採用試験小学全科3

お店でかき6個とりんご4個を買うと1340円になり、かき2個とりんご5個を買うと905円になる。りんご1個の値段はいくらか、①～⑤から一つ選んで番号で答えなさい。　　　　　　　　　　　　　　　　　　　　①125円②133円③140円④134円⑤110円　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　かき1個x円、りんご1個y円とすると、

正解は、肢①です。ここをポチッとお願いします。→"""
にほんブログ村"

旧国家Ⅱ種2

x人いたとして、ある人が抜けたことにより、平均点が2点下がってしまったとしましょう。　　　　　　　　　　　　　　　　　　　　このとき、ある人は、平均点よりも、2（x－1）点高い得点だったのです。　　　　　　　　　　　　　　　　　　　　また、ある人が抜けたことにより、平均点が3点上がったとすると、ある人は、平均点よりも3（x－1）点低い得点だったのです。　　　　　　　　　　　　　　　　　　　　　あるクラスで数学のテストを実施したところ、クラス全員の平均点はちょうど63点で、最も得点の高かったAを除いた平均点は62.2点、最も得点の低かったBを除いた平均点は63.9点、AとBの得点差はちょうど68点であった。このクラスの人数として正しいのはどれか。　　　　　　　　　　　　　　　　　　　　①29人②32人③35人④38人⑤41人　　　　　　　　　　　　　　　　　　　　　今、全体の平均点63＝0、クラスの人数をx人とします。　　　　　　　　　　　　　　　　　　　　Aを除くと平均点は0.8点下がってしまったので、Aは0.8（x－1）点です。　　　　　　　　　　　　　　　　　　　　また、Bを除くと、平均点は0.9点上がりました。ゆえに、Bの得点は－0.9（x－1）点です。　　　　　　　　　　　　　　　　　　　　その差が68点なので、0.8（x－1）＋0.9（x－1）＝68。1.7（x－1）＝68。x－1＝40。x＝41。正解は、肢⑤です。ここをポチッとお願いします。→
にほんブログ村

旧国家Ⅱ種1

往復コースを走ったり、泳いだりするレースで、はじめから終わりまで全く順序が入れ替わることがないときに限ってのことです。（そんなレースはまずないけど…）　　　　　　　　　　　　　　　　　　　　☆Aがn番目にBとすれ違ったならば、Bは前からn番目かn＋1番目を走ったり泳いだりしている。　　　　　　　　　　　　　　　　　　　　平成18年旧国家Ⅱ種より。　　　　　　　　　　　　　　　　　　　　　25mプールを図のように1コースが往路、2コースが復路とし、A～Fの6人が縦一列で往復した。次のア～エが分かっているとき確実にいえるのはどれか。　　　　　　　　　　　　　　　　　　　　ア　スタートしてからゴールするまで順序が入れ替わることはない。　　　　　　　　　　　　　　　　　　　　イ　Aが最初にすれ違ったのはCであり、Cが最初にすれ違ったのはAである。　　　　　　　　　　　　　　　　　　　　ウ　Bが最後にすれ違ったのはFであり、Fが最後にすれ違ったのはBである。　　　　　　　　　　　　　　　　　　　　エ　Dが3番目にすれ違ったのはEであり、4番目にすれ違ったのはFである。　　　　　　　　　　　　　　　　　　　　①1番前はAである。　　　　　　　　　　　　　　　　　　　　②前から2番目はCである。　　　　　　　　　　　　　　　　　　　　③前から3番目はEである。　　　　　　　　　　　　　　　　　　　　④後ろから3番目はDである。　　　　　　　　　　　　　　　　　　　　⑤後ろから2番目はFである。　　　　　　　　　　　　　　　　　　　　条件アより、この公式が使えます。　　　　　　　　　　　　　　　　　　　　条件イより、CとAは共に1位か2位。　　　　　　　　　　　　　　　　　　　　条件ウより、FとBは共に5位か6位。　　　　　　　　　　　　　　　　　　　　条件エより、Eは3位か4位で、Fは4位か5位。　　　　　　　　　　　　　　　　　　　　すると、Fは5位か6位でもあるし、4位か5位でもあるのだから、5位。正解は、肢⑤です。　　　　　　　　　　　　　　　　　　　　もう少しやってみると、Fが5位と決まれば、自動的にBは6位。1位2位は、どちらがCでどちらがAかは決まりません。3位4位も、どちらがDでどちらがEか決まりません。　　　　　　　　　　　　　　　　　　　　ここをポチッとお願いします。→
にほんブログ村