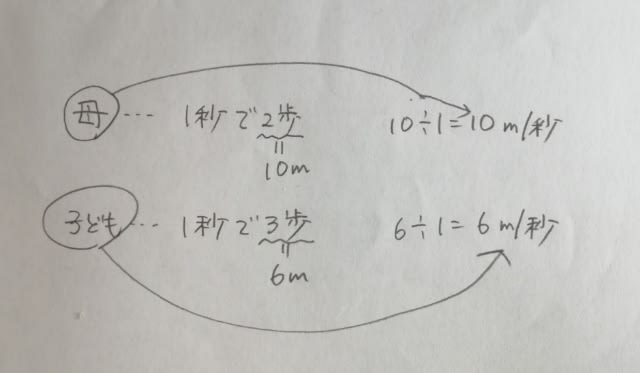
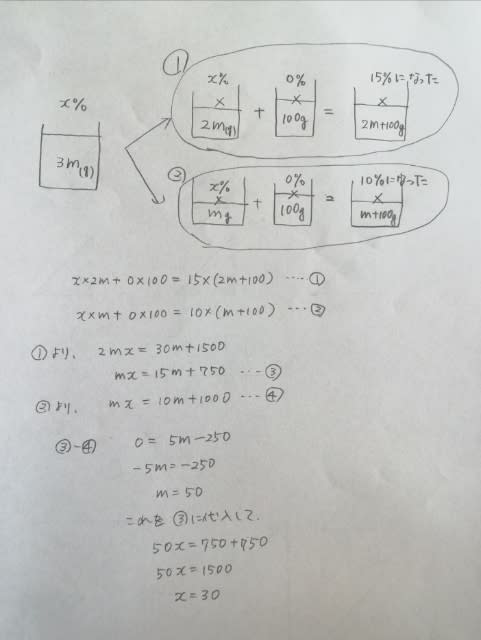
モグラの人形をハンマーでたたくゲームがあり、モグラは図のように配置された九つの穴A〜Iから出現する。あるときのモグラの出現順序について次のことが分かっているとき、正しく言えるのはどれか。
・各穴にモグラが1匹ずつ潜んでおり、各モグラは1度だけ出現した。 ・モグラが出現した回数は5回であり、うち4回は二つの穴から同時に出現し、残りの1回はCからのみ出現した。 ・モグラが出現した5回のうちで、四隅の穴(A、C、G、I)のうち少なくとも一つの穴からモグラが出現したのは3回であった。また、四隅の穴から出現した回が連続したことはなかった。 ・C、F、Iからは互いに異なる回にモグラが出現し、その3回は連続していた。また、G、H、Iからは互いに異なる回にモグラが出現し、その3回は連続していた。 ・IのモグラはBのモグラよりも先に出現し、BのモグラはDのモグラよりも先に出現した。 ①Bのモグラは3回目に出現した。 ②Eのモグラは2回目に出現した。 ③Aのモグラが出現した回とDのモグラが出現した回は連続していた。 ④Bのモグラが出現した回とCのモグラが出現した回は連続していた。 ⑤Eのモグラが出現した回とHのモグラが出現した回は連続していた。 こんな表で考えます。
モグラ出現表ですね。3つ目の条件より、四隅の穴から出てきたのは、1回目と3回目と5回目です。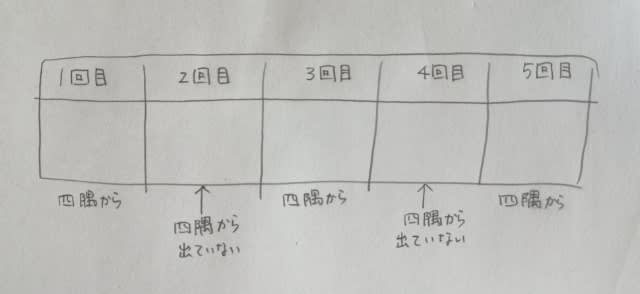
4つ目の条件で、C、F、Iは連続ということですが、CとIが四隅で、Fは四隅ではないことを考慮すると、CFIの順か、IFCの順であり、G、H、Iが連続だから、同様に考えると、GHIの順か、IHGの順です。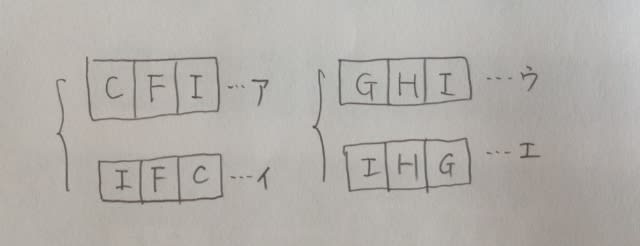
どちらにもIがいます。仮に、アとウを重ねると、ダメだこりゃですね。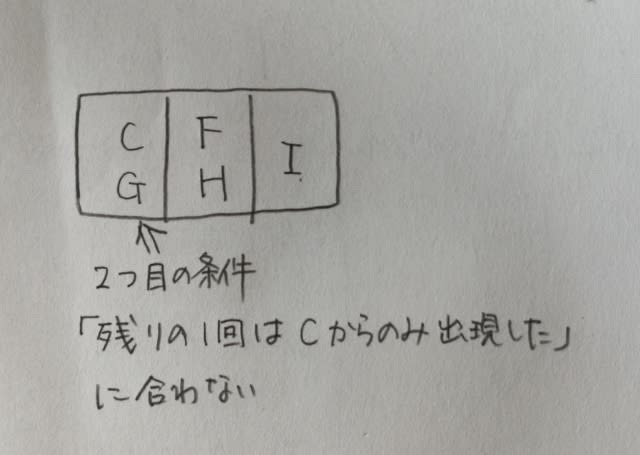
イとエを重ねても同じ理由でダメ。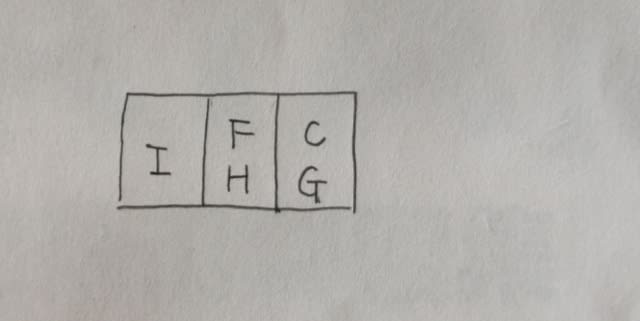
次に、イとウを重ねると、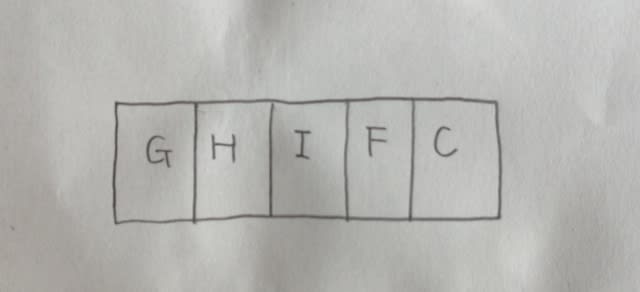
ところが、最後(5つ目)の条件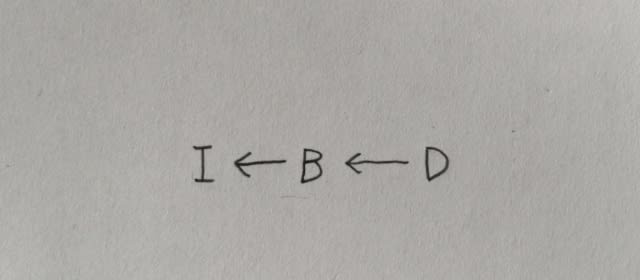
があるので、またもや、2つ目の条件に違反してしまいます。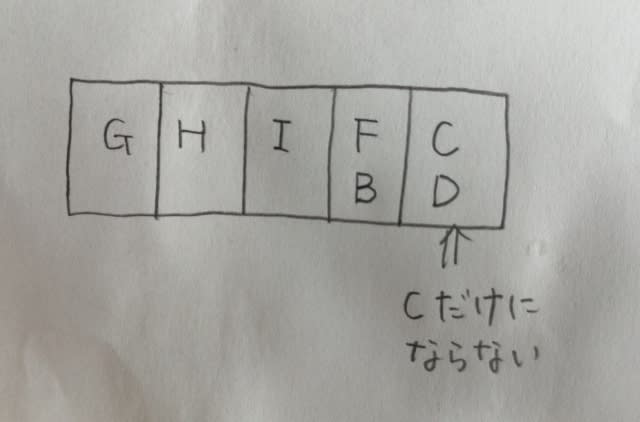
なので、アとエを重ねるしかありません。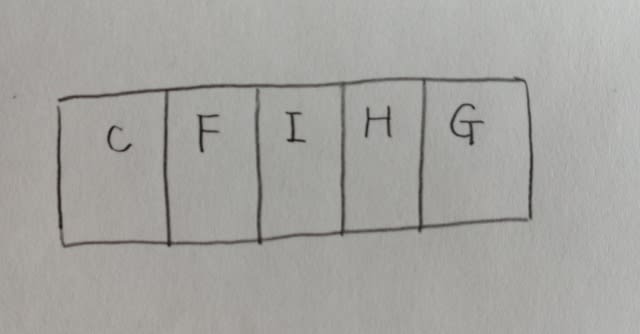
これに最後の条件を加えて、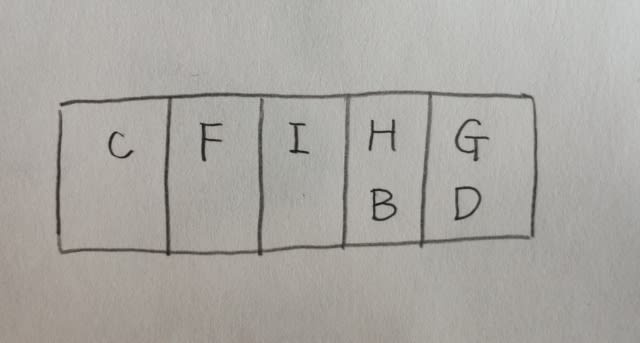
残るモグラは、AとEです。1回目はCだけしか出現していません(2つ目の条件)。2回目は、四隅から出現していない回なので、ここにEを入れて、3回目にAを入れれば出来上がりですね。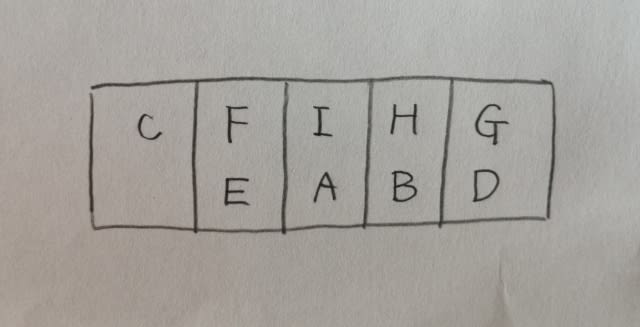

正解は、肢②です。ここをポチッとお願いします。→

・各穴にモグラが1匹ずつ潜んでおり、各モグラは1度だけ出現した。 ・モグラが出現した回数は5回であり、うち4回は二つの穴から同時に出現し、残りの1回はCからのみ出現した。 ・モグラが出現した5回のうちで、四隅の穴(A、C、G、I)のうち少なくとも一つの穴からモグラが出現したのは3回であった。また、四隅の穴から出現した回が連続したことはなかった。 ・C、F、Iからは互いに異なる回にモグラが出現し、その3回は連続していた。また、G、H、Iからは互いに異なる回にモグラが出現し、その3回は連続していた。 ・IのモグラはBのモグラよりも先に出現し、BのモグラはDのモグラよりも先に出現した。 ①Bのモグラは3回目に出現した。 ②Eのモグラは2回目に出現した。 ③Aのモグラが出現した回とDのモグラが出現した回は連続していた。 ④Bのモグラが出現した回とCのモグラが出現した回は連続していた。 ⑤Eのモグラが出現した回とHのモグラが出現した回は連続していた。 こんな表で考えます。

モグラ出現表ですね。3つ目の条件より、四隅の穴から出てきたのは、1回目と3回目と5回目です。

4つ目の条件で、C、F、Iは連続ということですが、CとIが四隅で、Fは四隅ではないことを考慮すると、CFIの順か、IFCの順であり、G、H、Iが連続だから、同様に考えると、GHIの順か、IHGの順です。
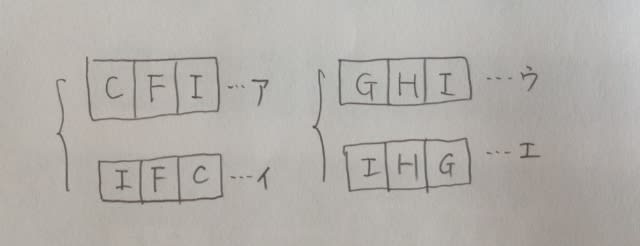
どちらにもIがいます。仮に、アとウを重ねると、ダメだこりゃですね。

イとエを重ねても同じ理由でダメ。

次に、イとウを重ねると、

ところが、最後(5つ目)の条件
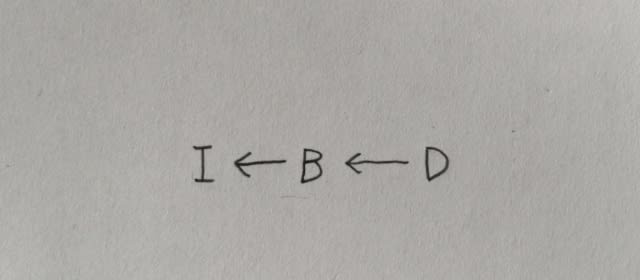
があるので、またもや、2つ目の条件に違反してしまいます。

なので、アとエを重ねるしかありません。

これに最後の条件を加えて、
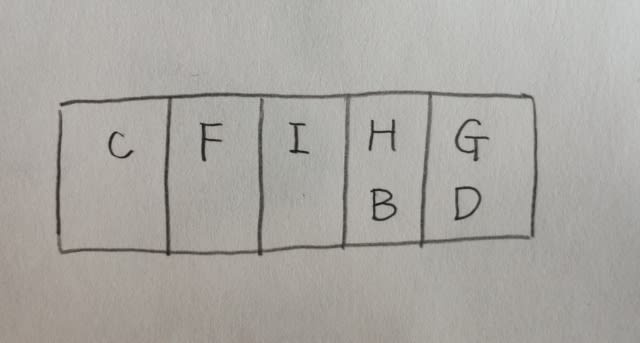
残るモグラは、AとEです。1回目はCだけしか出現していません(2つ目の条件)。2回目は、四隅から出現していない回なので、ここにEを入れて、3回目にAを入れれば出来上がりですね。


正解は、肢②です。ここをポチッとお願いします。→
にほんブログ村