中学入試の図形の問題は、公務員試験で、数的推理や空間把握として、ほとんど同じような問題が出題されます。 むしろ、逆に、公務員試験の知能の問題を中学入試で出題しているのかもしれません。 その方が、知能指数が高い子供を集めることができる? さて、今回は初級〜中級向けの問題です。 下の図のように、半径12cmの半円を2つの部分に分けました。 斜線部分の面積は何cm²ですか。 ただし、円周率は3.14とします。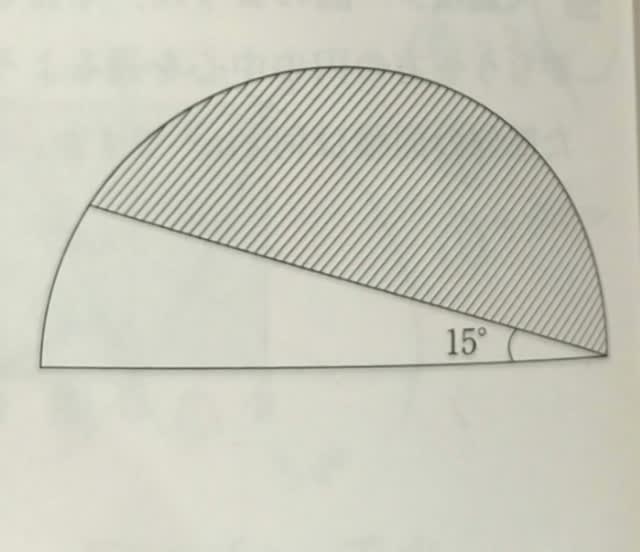
まあ、自分が小学生だったとしたら、間違いなくこうしたと思います。
しかし、これは間違い。㋐は、扇形ではありません。
とすると、㋐は、分割してみようかと考えます。(自分の勝手な考えだけど) それでは解いていこうと思うのですが、まず、大人の場合。
扇形OCBの面積から三角形COBの面積を引けば斜線部の面積は分かりますが、三角形COBの面積が出ません。(実は、1/2×12×12×sin150°で出るのですが、ここは中学の数学までしか使わないとして) 三角形COBの底辺は12cmで、高さを知りたいので、Cから直線ABに対して垂線を下ろします。 すると、たまたま∠COAが30°ですから、高さは6cmと判明します。
よって、こういうことになります。 正解は、152.4㎝²です。
正解は、152.4㎝²です。
小学生もほぼ同じ解き方です。 中学入試をする子は、三角定規の各辺の比率について、以下のことは知っています。(塾で習う)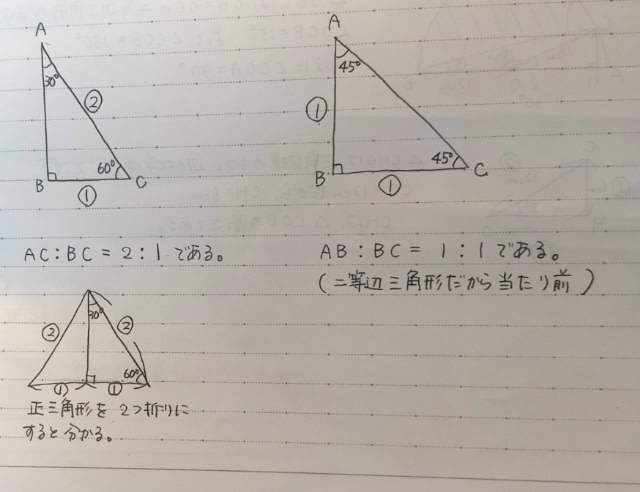
また、円周率を含む計算で、いちいち3.14を掛けていてはしんどいので、例えば、13×3.14−7×3.14などは、πを使い、13π−7π=6π=6×3.14=18.84とするトレーニングを塾でやります。 だから、大人とほぼ同じことになっちゃうんですね~。 こんな感じ。
自分のようなおじさんにはできませんが、子供は大変暗記が得意なので、2π=6.28、3π=9.42、4π=12.56、…………と、9π=28.26くらいまで暗記しておいて、本問などは、6π=18.84だから、60π=188.4。 そこから36を引いて152.4だ、などと、暗算で答えを出したりするので、おじさんはそんな子供と対戦すると、必ず負けます。





まあ、自分が小学生だったとしたら、間違いなくこうしたと思います。

しかし、これは間違い。㋐は、扇形ではありません。

とすると、㋐は、分割してみようかと考えます。(自分の勝手な考えだけど) それでは解いていこうと思うのですが、まず、大人の場合。

扇形OCBの面積から三角形COBの面積を引けば斜線部の面積は分かりますが、三角形COBの面積が出ません。(実は、1/2×12×12×sin150°で出るのですが、ここは中学の数学までしか使わないとして) 三角形COBの底辺は12cmで、高さを知りたいので、Cから直線ABに対して垂線を下ろします。 すると、たまたま∠COAが30°ですから、高さは6cmと判明します。

よって、こういうことになります。
 正解は、152.4㎝²です。
正解は、152.4㎝²です。小学生もほぼ同じ解き方です。 中学入試をする子は、三角定規の各辺の比率について、以下のことは知っています。(塾で習う)

また、円周率を含む計算で、いちいち3.14を掛けていてはしんどいので、例えば、13×3.14−7×3.14などは、πを使い、13π−7π=6π=6×3.14=18.84とするトレーニングを塾でやります。 だから、大人とほぼ同じことになっちゃうんですね~。 こんな感じ。

自分のようなおじさんにはできませんが、子供は大変暗記が得意なので、2π=6.28、3π=9.42、4π=12.56、…………と、9π=28.26くらいまで暗記しておいて、本問などは、6π=18.84だから、60π=188.4。 そこから36を引いて152.4だ、などと、暗算で答えを出したりするので、おじさんはそんな子供と対戦すると、必ず負けます。