2021年出題。 Aさん、Bさん、Cさんの3人は、それぞれのペースでP地点からQ地点、R地点を経由し、最後にS地点に達する一本道を、道に沿って歩き続けた。 下図は、この一本道を示した模式図であり、Q地点からR地点にかけては傾斜が急な山道が続く。 Aさん、Bさん、Cさんの3人は、12時00分に同時にP地点を出発し、Q地点、R地点、S地点を通過したときの時刻をそれぞれ記録した。 下の表はその結果をまとめたものであるが、CさんはQ地点を通過したときの時刻を記録することを忘れてしまったため、そこだけ記録が書かれていない。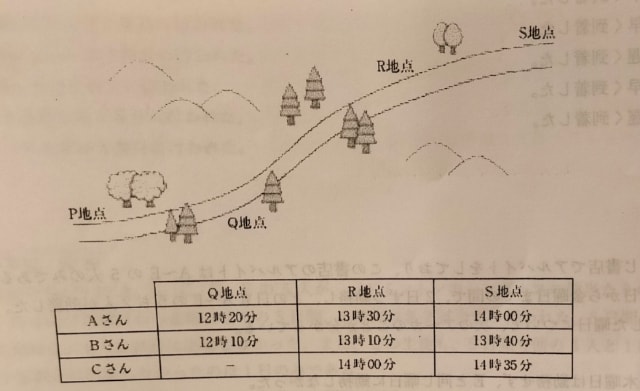
CさんがP地点からQ地点に行くまでにかかった時間よりも、CさんがQ地点からR地点に行くまでにかかった時間の方が長かった場合、確実にいえるものはどれか。①〜⑤から一つ選べ。 ただし、Aさん、Bさん、Cさんは3人とも、途中で道を引き返すことはなく、出発したその日のうちにS地点を通過したものとする。 ①AさんがQ地点を通過する前に、CさんはQ地点を通過した。 ②BさんがR地点を通過した後に、CさんはQ地点を通過した。 ③CさんがQ地点からS地点に行くまでにかかった時間は、Aさん、Bさん、Cさんの3人の中で、最も短かった。 ④12時30分の時点では、Aさん、Bさん、Cさんの3人ともQ地点からR地点の間にいた。 ⑤13時00分の時点では、Aさん、Bさん、Cさんの3人ともQ地点からR地点の間にいた。 Q地点からR地点にかけては傾斜が急な山道が続くとありますが、本問には関係ありません。 3人が各地点を通過した時刻は、
Cさんは、P地点からR地点までちょうど2時間かかっています。 P〜QよりもQ〜Rのほうが時間がかかったと問題に書いてあります。 だから、Cさんは、13時以前にQ地点を通過していますね。
肢①CさんがQ地点を通過したのは13時以前なのだが、AさんがQ地点を通過した12:20より前か後かは分かりません。 肢②BさんがR地点を通過したのは13:10。CさんがQ地点を通過したのは13:00以前だから、間違い。 肢③CさんはQ〜Rを進むのに60分よりも多くかかっているのですが、Aさん(70分)よりも短い時間だったか長い時間だったかは不明。 肢④例えば、CさんがP〜Qを40分で進んだとしたら、12時30分の時点では、CさんはQ地点からR地点の間にはいません。肢⑤13時には、AさんとBさんは確かにQ地点からR地点の間にいますね。 Cさんも、13時以前にQ地点を通過し、14時にR地点を通過するので、確かにQ地点からR地点の間にいます。 正解は、肢⑤です。


CさんがP地点からQ地点に行くまでにかかった時間よりも、CさんがQ地点からR地点に行くまでにかかった時間の方が長かった場合、確実にいえるものはどれか。①〜⑤から一つ選べ。 ただし、Aさん、Bさん、Cさんは3人とも、途中で道を引き返すことはなく、出発したその日のうちにS地点を通過したものとする。 ①AさんがQ地点を通過する前に、CさんはQ地点を通過した。 ②BさんがR地点を通過した後に、CさんはQ地点を通過した。 ③CさんがQ地点からS地点に行くまでにかかった時間は、Aさん、Bさん、Cさんの3人の中で、最も短かった。 ④12時30分の時点では、Aさん、Bさん、Cさんの3人ともQ地点からR地点の間にいた。 ⑤13時00分の時点では、Aさん、Bさん、Cさんの3人ともQ地点からR地点の間にいた。 Q地点からR地点にかけては傾斜が急な山道が続くとありますが、本問には関係ありません。 3人が各地点を通過した時刻は、

Cさんは、P地点からR地点までちょうど2時間かかっています。 P〜QよりもQ〜Rのほうが時間がかかったと問題に書いてあります。 だから、Cさんは、13時以前にQ地点を通過していますね。

肢①CさんがQ地点を通過したのは13時以前なのだが、AさんがQ地点を通過した12:20より前か後かは分かりません。 肢②BさんがR地点を通過したのは13:10。CさんがQ地点を通過したのは13:00以前だから、間違い。 肢③CさんはQ〜Rを進むのに60分よりも多くかかっているのですが、Aさん(70分)よりも短い時間だったか長い時間だったかは不明。 肢④例えば、CさんがP〜Qを40分で進んだとしたら、12時30分の時点では、CさんはQ地点からR地点の間にはいません。肢⑤13時には、AさんとBさんは確かにQ地点からR地点の間にいますね。 Cさんも、13時以前にQ地点を通過し、14時にR地点を通過するので、確かにQ地点からR地点の間にいます。 正解は、肢⑤です。














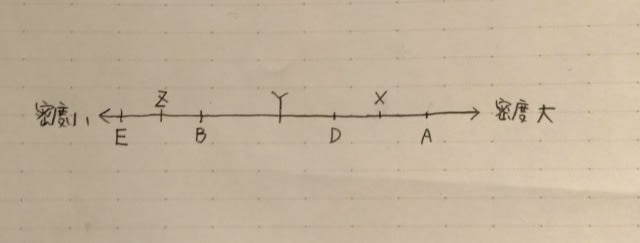
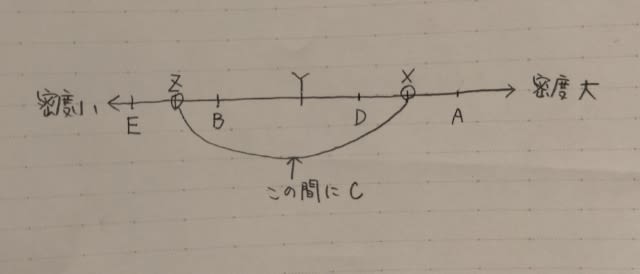




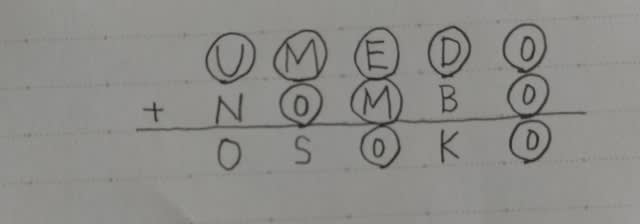


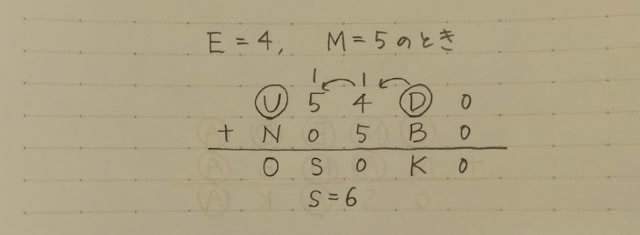



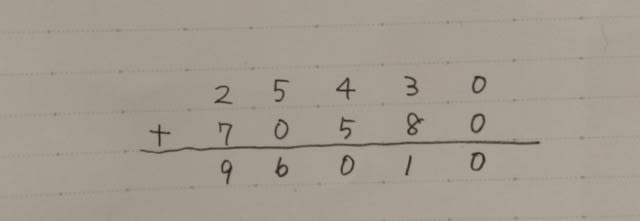


 すると、シュークリームの数が3個増えました! わざわざビックリマークを付けるほどのことではなく、まあ、7人のうちの1人が、2個買うのをやめて5個買ったんだと考えれば3個増えるのは当たり前のことですね。 以下、表を最後まで書くと、
すると、シュークリームの数が3個増えました! わざわざビックリマークを付けるほどのことではなく、まあ、7人のうちの1人が、2個買うのをやめて5個買ったんだと考えれば3個増えるのは当たり前のことですね。 以下、表を最後まで書くと、






