引き続き、大阪府教員チャレンジテストからです。 毎日営業しているレストランがある。このレストランには4人の従業員A～Dがおり、それぞれが週4日決まった曜日に出勤している。 この4人の出勤について次のア～オのことが分かっている。 ア 土曜日と日曜日は3人ずつ、ほかの曜日は2人ずつ出勤する。 イ Aは日曜日と金曜日に出勤する。 ウ BとCは1日だけ一緒に出勤する。 エ Cは日曜日に出勤する。 オ 4人とも3日間連続の出勤はしない。 このとき、4人の出勤について確実にいえるものはどれか。①～⑤から一つ選べ。 ①Aは木曜日に出勤する。 ②Dは火曜日に出勤する。 ③AとCの2人が水曜日に出勤しているときは、BとDの2人は木曜日に出勤している。 ④AとCの2人が木曜日に出勤しているときは、BとDの2人は水曜日に出勤している。 ⑤AとDは2日だけ一緒に出勤する。 まずは勤務表を作ります。
条件を記入します。
Aさんは土曜日に出勤すると、3連勤になっちゃうので、お休み。よって、土曜日はBとCとDの3人が出勤ですね。
BとCは、1日だけ一緒ということですが、それは土曜日です。よって、その他の曜日は、決して一緒に出勤しません。ゆえに、日曜日にBは出勤しません。日曜日はAとCとDが出勤です。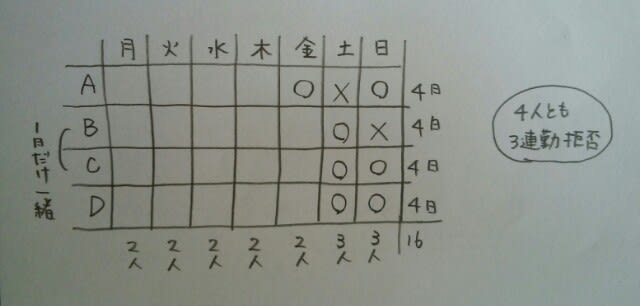
CとDは、土曜日、日曜日連勤ですから、当然、金曜日と月曜日の出勤を拒否してくるはずです。
ということで、金曜日はAとB、月曜日はAとBが出勤。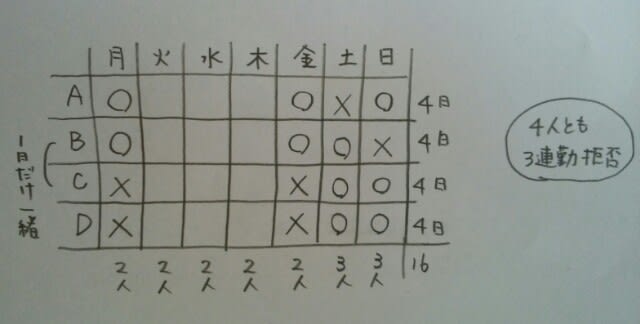
すると、Bは、金曜日と土曜日の連勤になっちゃうので、木曜日の出勤を拒否、Aは日曜日と月曜日の連勤なので、火曜日は休ませて下さいと言ってくるに決まってます。
もしも、Dさんが、火曜日にはヨガ教室があるから来れませんなどと言い出すと、BとCが2日一緒になってしまうので、Dさんにはヨガ教室は諦めてもらいます。
ここで、正解は、肢②と分かります。 でも、もう少し進めてみましょう。 実は、Cさんが、「木曜日に英会話教室に行くので……」などと言い出した場合、Cさんにも諦めてもらわなければいけないのです。なぜなら、木曜日にCさんがお休みすると、AとDが出勤となり、もうAとDは4日働いたので、水曜日は来れません。またもやBとCが一緒になってしまいます。でも、これは少々気が付きにくいですね。なので、はじめの段階で、次のようにしておきます。
確定するのは、ここまでです。
選択肢③がありますので、仮に、AとCが水曜日に出勤したとすると、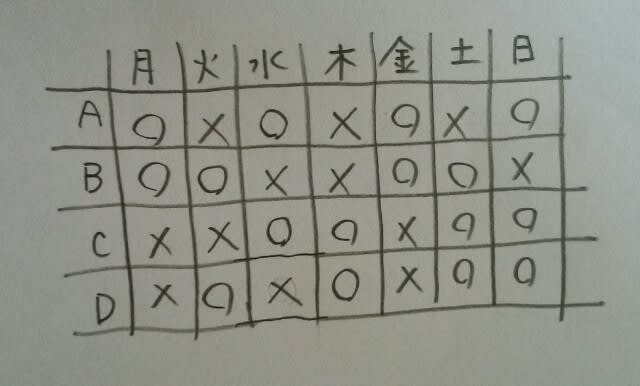
肢①と肢③と肢⑤の反例が出来上がりました。AとCが木曜日なら、
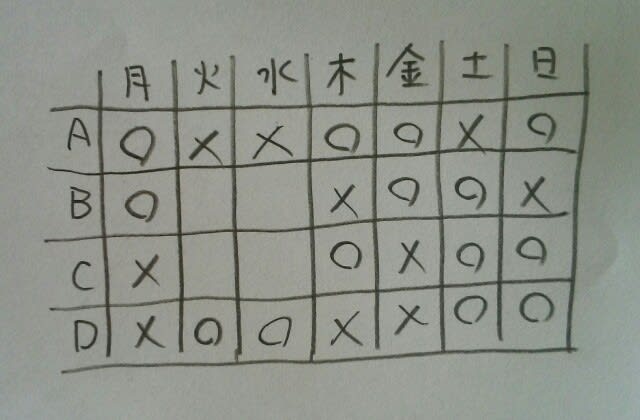このとき、確かにBとDが水曜日になることは、あり得ますが、確実だとはいえません。（火曜日になるかもしれない）普通、教員採用の一般知能は、公務員試験初級（高卒）程度のレベルなのですが、大阪府教員の場合は、上級程度の問題が出ます。大阪府教員を目指す皆さん、頑張って下さい！ここをポチッとお願いします。→
にほんブログ村
2018年1月実施の、大阪府教員チャレンジテストからです。 次の表1はある中学校のある日の2年1～4組の午前中の授業の時間割であり、表2はこの日の2年1～4組の授業担当教諭の午前中の時間割である。 この日の午後には、行事が行われる予定となっており、表1、表2の時間割について次のⅠ～Ⅳのことが分かっている。 
E教諭のわがままで、3組の3時間目は理科です。
体育は、3組と4組がそろわないとできません。そこで体育教諭の時間割をみると、1時間目に移動するしかありません。
すると、どうでしょう。1時間目は1～4組すべて体育です。仕方がないので、1、2組の体育をどこかに移動します。体育教諭の時間割より、3時間目に移動するしかありません。
ところで、3、4組の数学は何処へ？数学は習熟度別だから、3、4組そろっていなければ。2時間目は1、2組が数学だから、4時間目にしましょう。先生の時間割をみてもOKです。
3組の2時間目は社会のままでいいですね。4組は、2時間目が理科で、3時間目が国語になるけど、先生は……おっ、1組の3時間目の国語が変更になったので、A先生空いてますね。とりあえず、3、4組はうまくいきました。
後は、1組の国語が1時間目、2組の社会が1時間目に移動できればいいのですが、先生は大丈夫か？ダメだったら、もうE教諭には行事の準備には来ないで下さいとキッパリとお断りを……おっ、だ、大丈夫ですう～。
確実にいえるのは、ア、イ、エ。正解は、肢1です。ここをポチッとお願いします。→
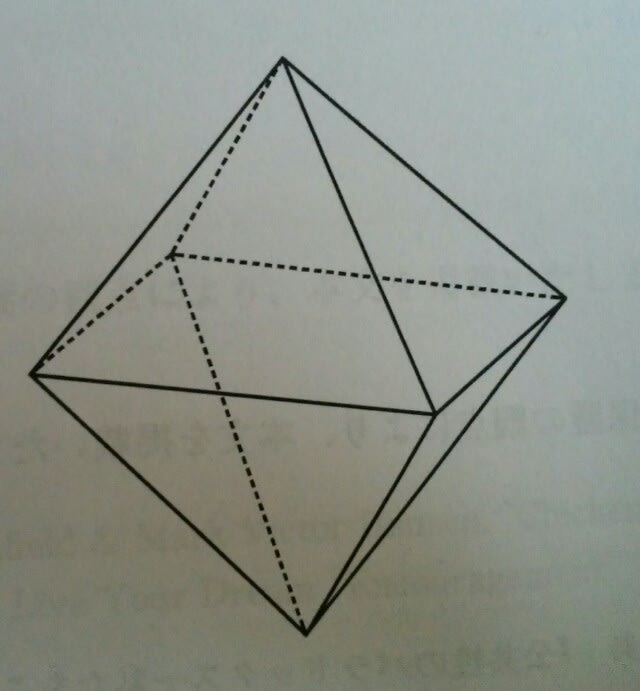
前回の記事のとおりで、正解は、肢5です。この種の問題は、とても多いのです。 それでは、発展問題です。平成9年度の国税専門官より。 かなり難解です。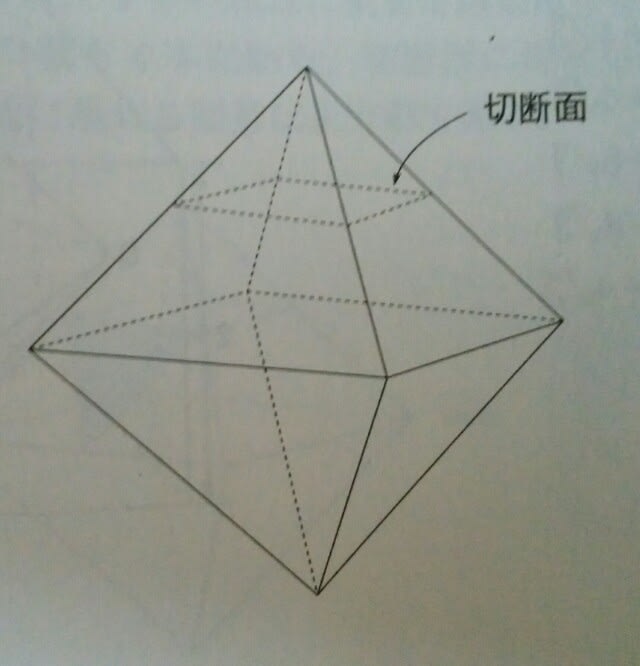 
①三角形 12個 ②三角形 18個 ③四角形 14個 ④四角形 18個 ⑤四角形 26個 数的推理では、「この操作を2回繰り返すと、～。」とか、「この操作を何回繰り返すと～になるか」は、よくありますし、空間把握でもたまにあります。 1回目の作業の後にできる立体は、正方形が6面と、正三角形が8面でできています。
この立体に、もう一度同じ作業をします。この立体（2回目の作業を行う前の立体）は、準正14面体といい、頂点が12個（①で考えたように、4×6÷2）、面が14面（6＋8）あります。ゆえに、
1回目の作業でできた準正14面体には、正三角形の面と正方形の面があり、正三角形の面では三角形が残り、正方形の面では四角形が残るので、かなり難しく感じる人が多いと思います。結局、四角形が18面と三角形が8面なので、正解は、肢④です。ここをポチッとお願いします。→
「またこれ！」というほどよく出題される問題です。 正八面体の各辺の中点をとり、次の図のように頂点に近い4つの点を結んだ線に沿って四角すいを切り落とす作業を、正八面体のすべての頂点について行った。このとき、後に残った立体の辺の本数として、正しいものはどれか。
①8本②12本③16本④20本⑤24本 辺の本数だけ求めればよいのですが、せっかくだから、面、辺、頂点すべての数を求めてみます。「後に残った立体の面、辺、頂点の数をすべて足すといくらになるか」などという問題もありそうです。 こういうときは、新旧方式で考えるのがお勧めです。まず辺から。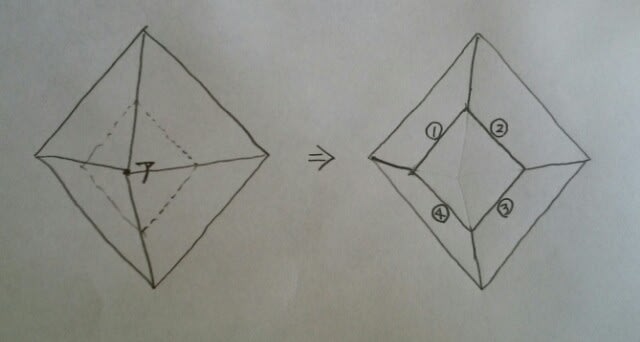
今、頂点アで四角すいを切り落としたところですが、①～④の4つの辺は、切り落とすことによってできた新しい辺ですね。そして、
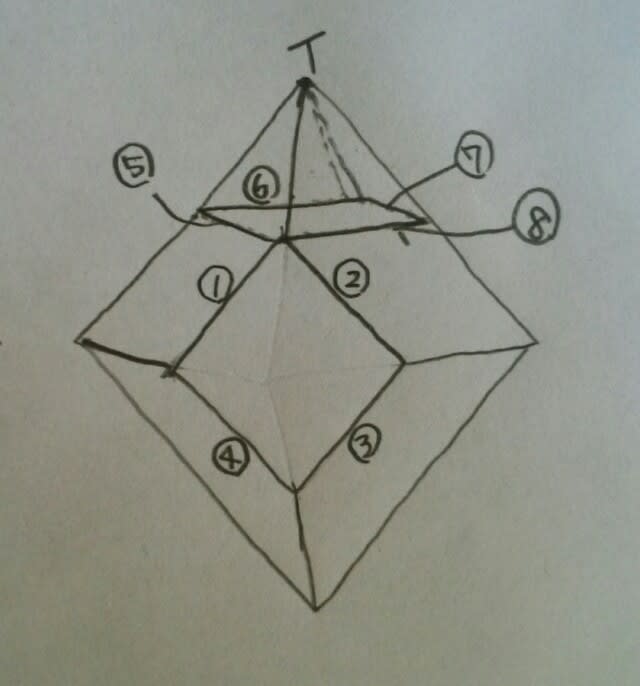頂点イで切り落とすと、また⑤～⑧の新しい辺ができます。そして、①～④と、⑤～⑧で、ダブっている辺はありません。 つまり、「一つの頂点で切り落とすごとに、新しい辺が4つずつできる」ことが分かります。正八面体には6つの頂点があるので、新しくできる辺の数は、4×6＝24です。では、もともとあった辺は、いくつ残るのでしょうか？
図の、A、Bは、四角すいを切り落としたときに消失します。よって、もともとあった辺は、すべて消失します。元の正八面体を構成していた辺は、一つも残らないのです。 以上より、後に残った立体の辺の数は、24＋0＝24。正解は、肢⑤です。頂点も、面も、同じように考えます。
新しくできる頂点の数は、4×6÷2＝12。（2つずつダブるので2で割りました）もともとあった頂点は、すべて消失。よって、12＋0＝12。
新しくできる面の数は、1×6＝6。もともとあった8面は、すべて残ります。よって、6＋8＝14。 ここをポチッとお願いします。→
平成23年の旧国家Ⅱ種より。 図Ⅰは、相対する面の数の和が7となるサイコロであり、これを前後、左右に何回か回転させた後に見ると、図Ⅱのようになった。
これと同じサイコロ8個を使って図Ⅲのような大きな立方体をつくり、これを図Ⅰ→図Ⅱとしたのと同じ要領で回転させた後に見ると、図Ⅳのようになった。 この場合、図Ⅲに矢印で示した2個のサイコロが、大きな立方体内で他のサイコロと接する面（それぞれ3面）の数を合計するといくらになるか。
①26②27③28④29⑤30 問題文中の、「同じ要領で回転させた」が気になりますねえ。 図Ⅰを、どのように転がせば、図Ⅱになるのか？まずは、これを解明しなくては……。というのが自然なのですが、実は全く関係ありません。（それでも気になる人は、最後に一例を挙げておきます。） 図Ⅰと図Ⅱを観察すると、
図Ⅰでは、頂点アに、1と4と5の目が集まっています。では、図Ⅱにおいて、頂点アは、どこでしょうか？
図Ⅰでは、頂点イに、2と4と6の目が集まっています。では、図Ⅱにおいて、頂点イは、どこでしょうか？
これと同じことを、図Ⅲ、図Ⅳですれば答えが分かります。
どちらのサイコロも、1と2と3の目が表面に出ているので、4と5と6の目は、大きな立方体内で、他のサイコロと接しています。よって、それらの目の合計は、（4＋5＋6）×2＝30。正解は、肢⑤です。ちなみに、図Ⅰから図Ⅱになるには、例えば、
なので、図Ⅲから図Ⅳは、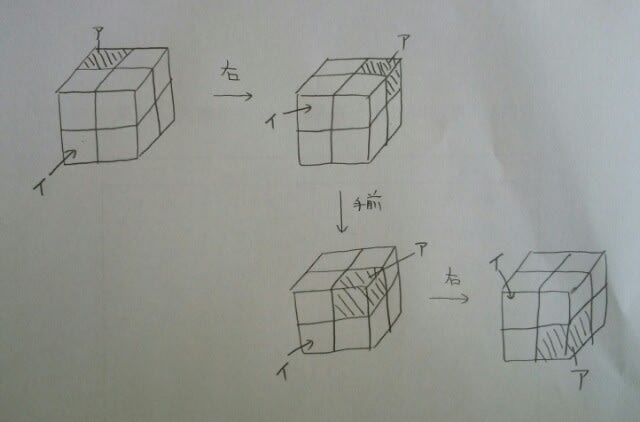
ここをポチッとお願いします。→