現在、父が46歳、長男が17歳、長女が14歳だとする。 父の年齢が二人の子の年齢の和よりも5歳多くなるのは何年後か? このような問題を年齢算といいます。 本問を表に表すと、
父の年齢が二人の年齢の和よりも5歳多くなるのはx年後だとしてみます。 例えば、今から7年後には、7歳年齢が増えています。 だから、x年後には、父も長男も長女も年齢がx歳増えています。
よって、次のような方程式ができます。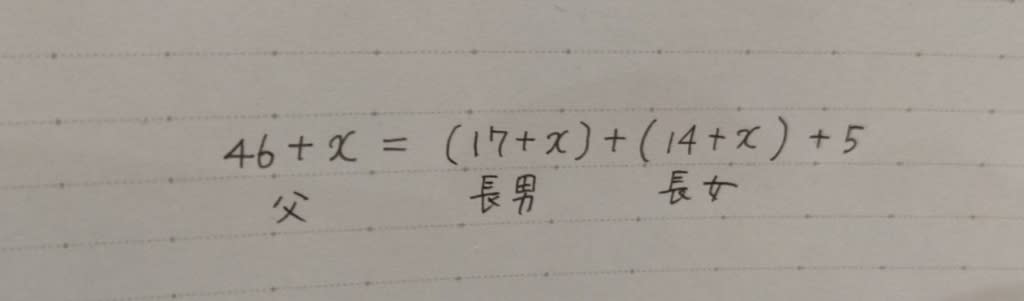
これを解くと、
正解は、10年後です。 算数では、全然違う考え方になります。 現在、父の年齢と二人の子の年齢の和を比べると、父の年齢の方が15歳多くなっています。 これが、来年にはどうなるでしょうか? 父が1歳増えても、長男が1歳年をとり、長女も1歳年をとるのだから、合わせて2歳増えます。 すると、今年は15歳の差があっても、来年は14歳の差になってしまいますね。
つまり、一年で1ずつ差が減っていく。 今、父のほうが15歳多いのだけれど、10年後には、父のほうが5歳多くなる。 ゆえに正解は10年後。 なのですが、全ての年齢算を、この考え方で解くことはできません。 方程式、算数、どちらの考え方もマスターしておくべきです。 「そんなこと言ったって、10年後のいつなのかによって、いろいろあんじゃないの~?」という疑問を持ったあなたはもはやプロ級! 現在というのが何月何日か、10年後と言っても、10年後の何月何日かによって、各人の誕生日というものがあるので、正確には本問のようにはならないことがあります。 しかし、それでは正解がいくつか出てきてしまうので、年齢算では、特に断りがない限り、同じ日付で考えます。 例えば、現在が1月1日なら、何年前でも何年後でも、それは、その年の1月1日として考えるのです。 だから、本問の解説のようにやっていっても構いません。









父の年齢が二人の年齢の和よりも5歳多くなるのはx年後だとしてみます。 例えば、今から7年後には、7歳年齢が増えています。 だから、x年後には、父も長男も長女も年齢がx歳増えています。

よって、次のような方程式ができます。
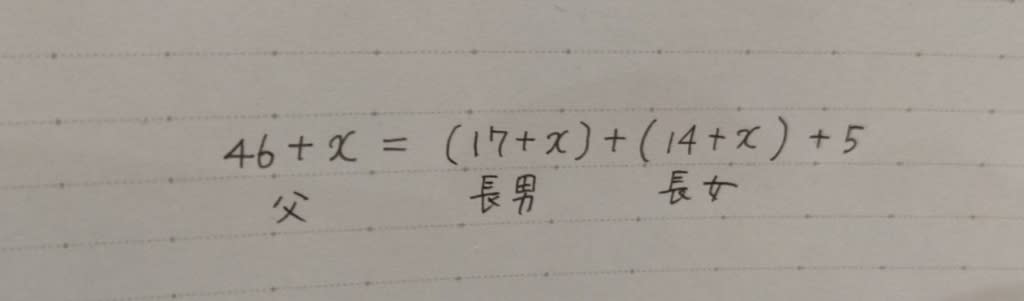
これを解くと、

正解は、10年後です。 算数では、全然違う考え方になります。 現在、父の年齢と二人の子の年齢の和を比べると、父の年齢の方が15歳多くなっています。 これが、来年にはどうなるでしょうか? 父が1歳増えても、長男が1歳年をとり、長女も1歳年をとるのだから、合わせて2歳増えます。 すると、今年は15歳の差があっても、来年は14歳の差になってしまいますね。

つまり、一年で1ずつ差が減っていく。 今、父のほうが15歳多いのだけれど、10年後には、父のほうが5歳多くなる。 ゆえに正解は10年後。 なのですが、全ての年齢算を、この考え方で解くことはできません。 方程式、算数、どちらの考え方もマスターしておくべきです。 「そんなこと言ったって、10年後のいつなのかによって、いろいろあんじゃないの~?」という疑問を持ったあなたはもはやプロ級! 現在というのが何月何日か、10年後と言っても、10年後の何月何日かによって、各人の誕生日というものがあるので、正確には本問のようにはならないことがあります。 しかし、それでは正解がいくつか出てきてしまうので、年齢算では、特に断りがない限り、同じ日付で考えます。 例えば、現在が1月1日なら、何年前でも何年後でも、それは、その年の1月1日として考えるのです。 だから、本問の解説のようにやっていっても構いません。



















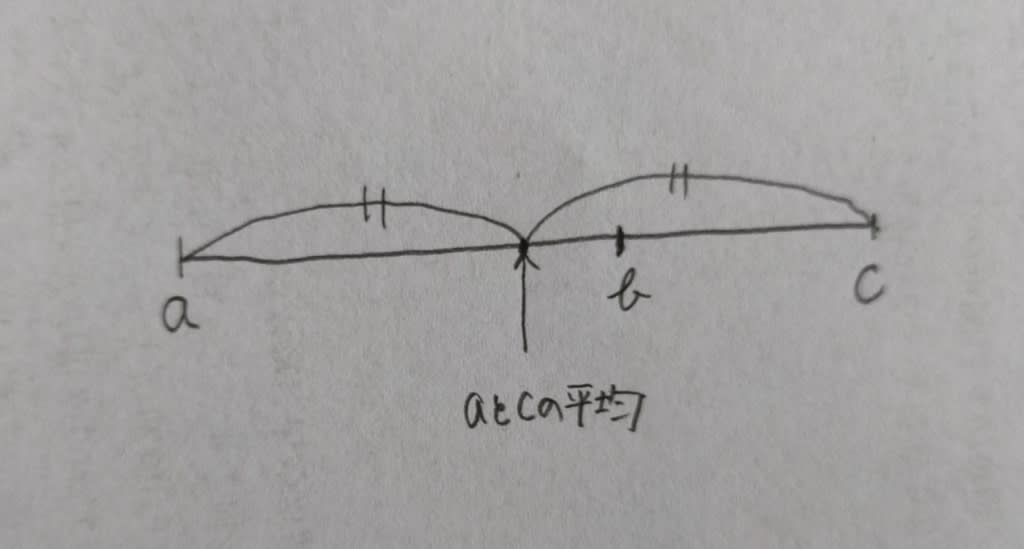 ここに、その他の条件も付け加えて、
ここに、その他の条件も付け加えて、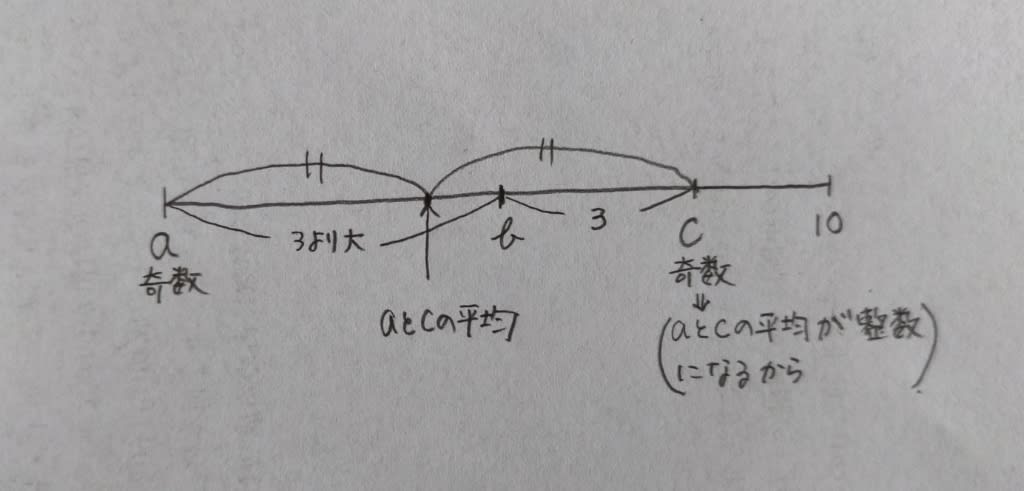












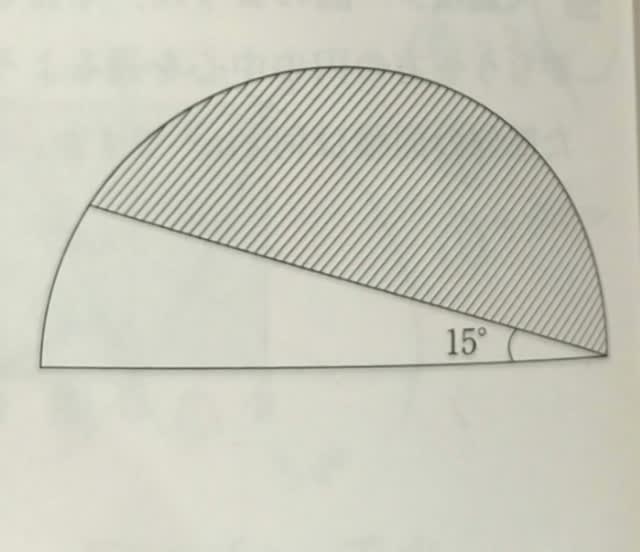




 正解は、
正解は、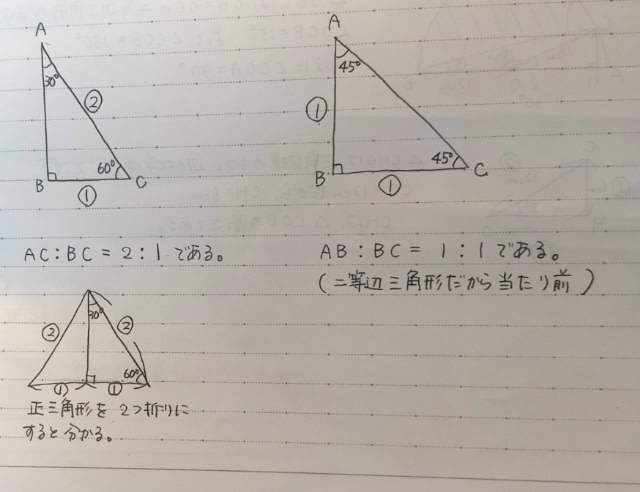








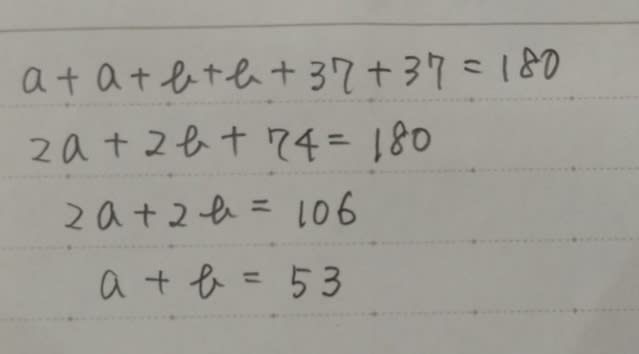 よって、∠BAD=53+33=86°。
よって、∠BAD=53+33=86°。












