正直者ってどんな人?ウソつきってどんな人?世間一般には、大事な場面で、ウソをつかない人を正直者といい、大事な場面で、ウソをつく人をウソつきといいます。 しかし、数学の世界では、我々は、ほとんど全員がウソつきなのです。子どもの頃、母親から、「もう宿題やったの?」と聞かれ、実はまだやってないのに、「やったよ。」とウソをついたことくらい、誰でもあるはずです。 つまり、生まれてから今まで、1回もウソをついていない人だけが正直者なのです。 だいぶ話がそれましたが、ここでは、正直者は、必ず本当のことをいい、ウソつきは、ウソしか言わないとします。 まず、Aさんが、「Bはウソつきだ」と発言したとしましょう。もしも、Aが正直者だったら、Aの発言は本当なので、Bはウソつきです。また、Aがウソつきだったら、Aの発言はウソなので、Bは正直者です。 次に、Aさんが、「Bは正直者だ」と発言したとしましょう。もしも、Aが正直者だったら、Aの発言は本当なので、Bは正直者です。Aがウソつきだったら、Aの発言はウソなので、Bもウソつきです。
次に、Aさんが、「Bは正直者だ」と発言したとしましょう。もしも、Aが正直者だったら、Aの発言は本当なので、Bは正直者です。Aがウソつきだったら、Aの発言はウソなので、Bもウソつきです。 ところで、この種の問題を考えるときには、登場人物を、2つのグループに分けます。
ところで、この種の問題を考えるときには、登場人物を、2つのグループに分けます。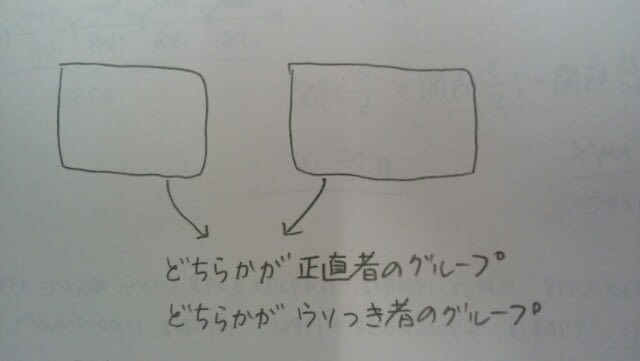
 ここまで、まとめます。○さんが、□さんのことを、「ウソつきだ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、違うグループになります。 また、○さんが□さんのことを「正直者だ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、同じグループになります。これを、
ここまで、まとめます。○さんが、□さんのことを、「ウソつきだ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、違うグループになります。 また、○さんが□さんのことを「正直者だ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、同じグループになります。これを、
GW法と言います。以下は、国家Ⅲ種の過去問です。 Aが、Bのことを正直者だといったので、AとBは同じグループ。BはCのことをウソつきだと言ったので、BとCは、違うグループ。Cは、Dのことをウソつきだと言ったので、CとDは違うグループ。よって、Dの発言は当然。
Aが、Bのことを正直者だといったので、AとBは同じグループ。BはCのことをウソつきだと言ったので、BとCは、違うグループ。Cは、Dのことをウソつきだと言ったので、CとDは違うグループ。よって、Dの発言は当然。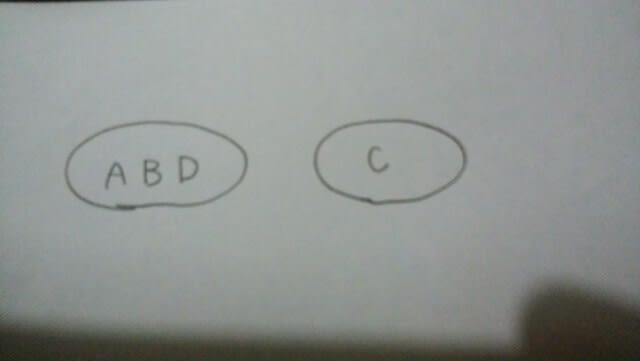 少なくとも2人が正しいことを言っているので、A、B、Dのいるグループが正直者。よって、正解は肢②です。次回、東京消防庁1類の過去問を紹介します。
少なくとも2人が正しいことを言っているので、A、B、Dのいるグループが正直者。よって、正解は肢②です。次回、東京消防庁1類の過去問を紹介します。

にほんブログ村
 次に、Aさんが、「Bは正直者だ」と発言したとしましょう。もしも、Aが正直者だったら、Aの発言は本当なので、Bは正直者です。Aがウソつきだったら、Aの発言はウソなので、Bもウソつきです。
次に、Aさんが、「Bは正直者だ」と発言したとしましょう。もしも、Aが正直者だったら、Aの発言は本当なので、Bは正直者です。Aがウソつきだったら、Aの発言はウソなので、Bもウソつきです。 ところで、この種の問題を考えるときには、登場人物を、2つのグループに分けます。
ところで、この種の問題を考えるときには、登場人物を、2つのグループに分けます。
 ここまで、まとめます。○さんが、□さんのことを、「ウソつきだ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、違うグループになります。 また、○さんが□さんのことを「正直者だ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、同じグループになります。これを、
ここまで、まとめます。○さんが、□さんのことを、「ウソつきだ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、違うグループになります。 また、○さんが□さんのことを「正直者だ」と言えば、○さんが本当のことを言ってようが、言ってなかろうが、○と□は、同じグループになります。これを、GW法と言います。以下は、国家Ⅲ種の過去問です。
 Aが、Bのことを正直者だといったので、AとBは同じグループ。BはCのことをウソつきだと言ったので、BとCは、違うグループ。Cは、Dのことをウソつきだと言ったので、CとDは違うグループ。よって、Dの発言は当然。
Aが、Bのことを正直者だといったので、AとBは同じグループ。BはCのことをウソつきだと言ったので、BとCは、違うグループ。Cは、Dのことをウソつきだと言ったので、CとDは違うグループ。よって、Dの発言は当然。 少なくとも2人が正しいことを言っているので、A、B、Dのいるグループが正直者。よって、正解は肢②です。次回、東京消防庁1類の過去問を紹介します。
少なくとも2人が正しいことを言っているので、A、B、Dのいるグループが正直者。よって、正解は肢②です。次回、東京消防庁1類の過去問を紹介します。
にほんブログ村










