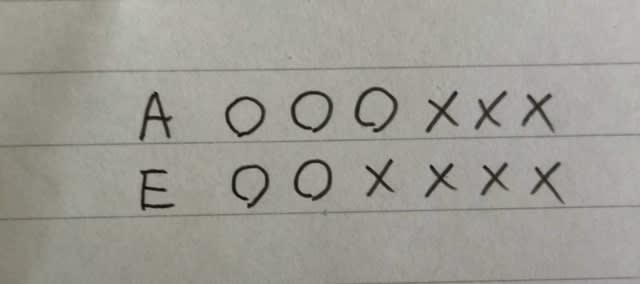2021年出題。 図Ⅰのような3✕3の中央が塞がった八つのマス目があり、ここにボールを収納していくことを考える。 次の条件を満たすようにボールを収納するとき、八つのマス目全体で収納できるボールの個数の最大値と最小値の差はいくらか。 ○いずれのマスにも最低1個のボールが入っている。 ○図Ⅱのように、一直線に並んだ三つのマスには、いずれも計9個のボールが入っている。
①6 ②8 ③10 ④12 ⑤14 最大値から考えてみます。
横向きに考えると、a+b+c=9と、f+g+h=9は動かせないので、ボールの個数を最大にするには、d、eに、できるだけ多くのボールを入れてやればよい。 縦向きに考えると、a+d+f=9、c+e+h=9は動かせないので、b、gに、できるだけ多くのボールを入れてやればよい。 一列9個だから、 でも、いずれのマスにも最低1個は入れなければいけないので、これは失敗😣。 じゃあ、とりあえず四隅のマスに1個ずつ入れておいてから、やり直し。
でも、いずれのマスにも最低1個は入れなければいけないので、これは失敗😣。 じゃあ、とりあえず四隅のマスに1個ずつ入れておいてから、やり直し。 空いてるマスには7個ずつ入れればOKですね。 これが最大になるときです。
空いてるマスには7個ずつ入れればOKですね。 これが最大になるときです。 全部で32個。 次に、最小値です。 最大値と同様に考えて、a+b+c=9、f+g+h=9は動かせないので、d、eにはできるだけ少ない個数(1個)を入れ、a+d+f=9、c+e+h=9は動かせないので、b、gにはできるだけ少ない個数(1個)入れます。
全部で32個。 次に、最小値です。 最大値と同様に考えて、a+b+c=9、f+g+h=9は動かせないので、d、eにはできるだけ少ない個数(1個)を入れ、a+d+f=9、c+e+h=9は動かせないので、b、gにはできるだけ少ない個数(1個)入れます。 一列を9個にする方法は何通りかあるのですが、一例として、こんなのがあります。
一列を9個にする方法は何通りかあるのですが、一例として、こんなのがあります。 全部で20個。 よって、最大値と最小値の差は、32−20=12。 正解は、肢④です。 実は、これとほぼ同じ問題が過去に出題されています。 めちゃくちゃ前です。 自分が把握していないだけで、最近も出題されていたかもだけど、とりあえず、載せときます。
全部で20個。 よって、最大値と最小値の差は、32−20=12。 正解は、肢④です。 実は、これとほぼ同じ問題が過去に出題されています。 めちゃくちゃ前です。 自分が把握していないだけで、最近も出題されていたかもだけど、とりあえず、載せときます。
正解は肢⑤。


①6 ②8 ③10 ④12 ⑤14 最大値から考えてみます。

横向きに考えると、a+b+c=9と、f+g+h=9は動かせないので、ボールの個数を最大にするには、d、eに、できるだけ多くのボールを入れてやればよい。 縦向きに考えると、a+d+f=9、c+e+h=9は動かせないので、b、gに、できるだけ多くのボールを入れてやればよい。 一列9個だから、
 でも、いずれのマスにも最低1個は入れなければいけないので、これは失敗😣。 じゃあ、とりあえず四隅のマスに1個ずつ入れておいてから、やり直し。
でも、いずれのマスにも最低1個は入れなければいけないので、これは失敗😣。 じゃあ、とりあえず四隅のマスに1個ずつ入れておいてから、やり直し。 空いてるマスには7個ずつ入れればOKですね。 これが最大になるときです。
空いてるマスには7個ずつ入れればOKですね。 これが最大になるときです。 全部で32個。 次に、最小値です。 最大値と同様に考えて、a+b+c=9、f+g+h=9は動かせないので、d、eにはできるだけ少ない個数(1個)を入れ、a+d+f=9、c+e+h=9は動かせないので、b、gにはできるだけ少ない個数(1個)入れます。
全部で32個。 次に、最小値です。 最大値と同様に考えて、a+b+c=9、f+g+h=9は動かせないので、d、eにはできるだけ少ない個数(1個)を入れ、a+d+f=9、c+e+h=9は動かせないので、b、gにはできるだけ少ない個数(1個)入れます。 一列を9個にする方法は何通りかあるのですが、一例として、こんなのがあります。
一列を9個にする方法は何通りかあるのですが、一例として、こんなのがあります。 全部で20個。 よって、最大値と最小値の差は、32−20=12。 正解は、肢④です。 実は、これとほぼ同じ問題が過去に出題されています。 めちゃくちゃ前です。 自分が把握していないだけで、最近も出題されていたかもだけど、とりあえず、載せときます。
全部で20個。 よって、最大値と最小値の差は、32−20=12。 正解は、肢④です。 実は、これとほぼ同じ問題が過去に出題されています。 めちゃくちゃ前です。 自分が把握していないだけで、最近も出題されていたかもだけど、とりあえず、載せときます。
正解は肢⑤。
















 肢④‥‥肢①と同様ですね。 1≦a≦3で、c=15だから、16≦a+c≦18。 AとCをした場合の電気代は必ず4000円/月になります。
肢④‥‥肢①と同様ですね。 1≦a≦3で、c=15だから、16≦a+c≦18。 AとCをした場合の電気代は必ず4000円/月になります。




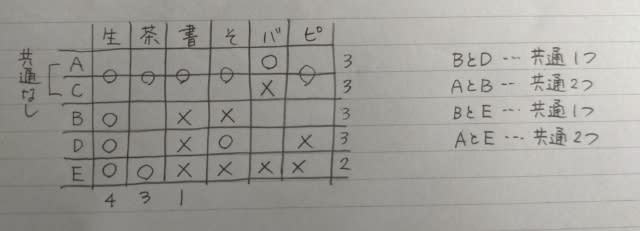
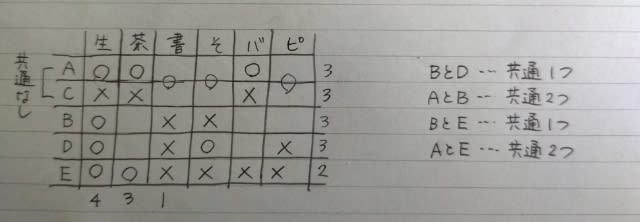
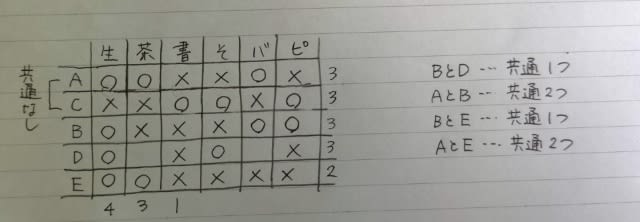
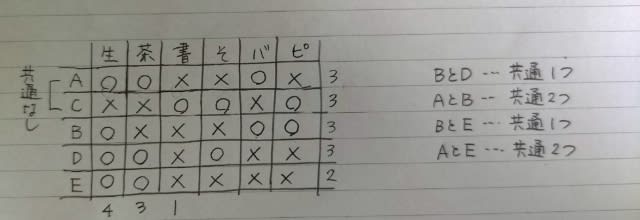
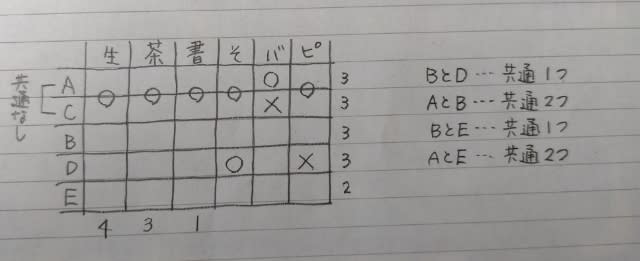
 Aの発言より、Aは、短距離走を終えたときにはBより上位でした。 ハードル走の間に一瞬Bに抜かれますが、すぐに抜き返してゴールしたのだから、結局ハードル走が終わったときにはやはりBより上位ですね。 さらにEの発言から、こうなります。
Aの発言より、Aは、短距離走を終えたときにはBより上位でした。 ハードル走の間に一瞬Bに抜かれますが、すぐに抜き返してゴールしたのだから、結局ハードル走が終わったときにはやはりBより上位ですね。 さらにEの発言から、こうなります。
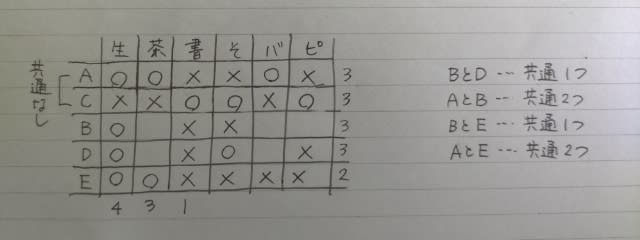
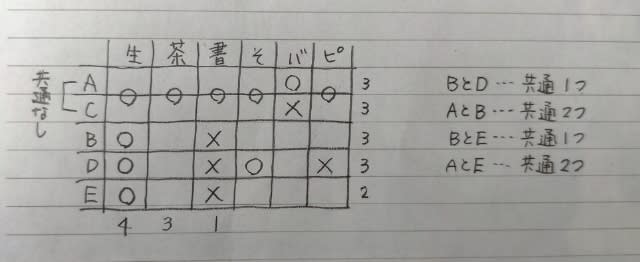
 このとき、Cは図の左(上位)にいたか、右(下位)にいたか? 左にいたとすると、CはDを抜いたときに1位になり、Cの発言がまたまた嘘になるので、右側にいたのです。 つまり、Cは短距離走では5位で、Dのみを抜いて最終4位。
このとき、Cは図の左(上位)にいたか、右(下位)にいたか? 左にいたとすると、CはDを抜いたときに1位になり、Cの発言がまたまた嘘になるので、右側にいたのです。 つまり、Cは短距離走では5位で、Dのみを抜いて最終4位。











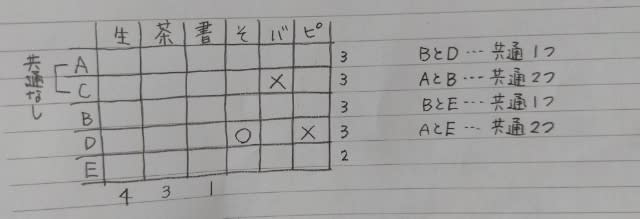
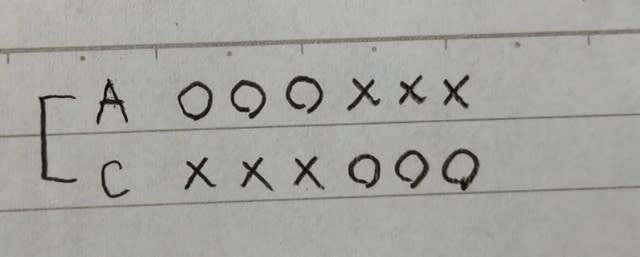
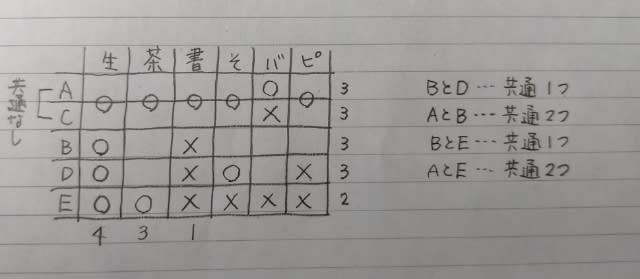 ここで肢⑤はダメ。
ここで肢⑤はダメ。