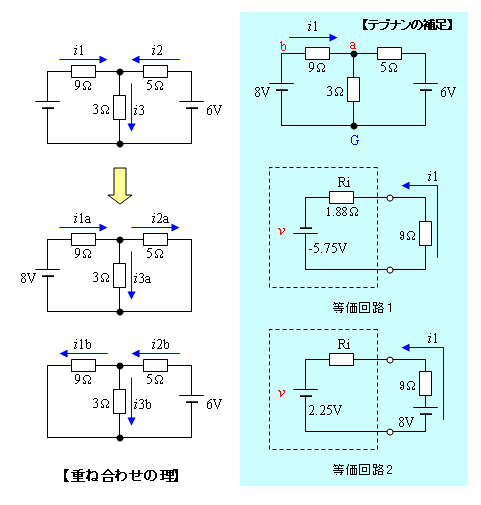
(キルヒホッフにて i1=0.53 i2=0.55 i3=1.08 )
【重ね合わせの理】
テブナンの定理を使うことで電気回路の計算がずいぶん楽になりましたが、もうひとつ「重ね合わせの理」という妙手があります。やってみましょう。
左上の図が元回路です。これを中の図、下の図のように片方の電源を短絡して各電流を求めてみます。
8Vの電源から流れる電流は
i1a=8/(9+15/8) =0.74
i2a=0.74×3/8 =0.28 → -0.28(i2に対して逆)
i3a=0.74-0.28 =0.46
6Vの電源から流れる電流は
i2b=6/(5+27/12) =0.83
i1b=0.83×3/12 =0.21 → -0.21(i1に対して逆)
i3b=0.83-0.21 =0.62
そして、電流aと電流bを足します。この重ねあわせに“理”があります。
i1=i1a+i1b =0.74-0.21 =0.53
i2=i2a+i2b =-0.28+0.83 =0.55
i3=i3a+i3b =0.46+0.62 =1.08
となって、キルヒホッフで求めた各電流と一致しましたね。
何か狐につままれたような感じですが、これが「重ね合わせの理」です。
すごいっすね。(^^)
[テブナンの定理の補足]
右列の図を見てください。テブナンの定理を使って、9Ωに流れる電流i1を求めてみましょう。
ルールに沿って9Ωを取払い、まずa-b間電圧を求めます。これは8Vが直列に入るので少しややこしいですが、a-G間電を求めて8Vを引けばa-b間電圧になりますね。OKですか?(^^)
V(a-b)=6×(3/8)-8
V(a-b)=2.25-8 =-5.75
端子a-bから見た回路インピーダンスは5Ωと3Ωの並列ですから、
Ri=15/8 =1.88Ω
よって、元の回路は等価回路1に置き換えられます。
故に、 i1=-5.75/(1.88+9) よって
i1=-0.53
マイナスが付いているのは、電流がb→aに流れているということです。よって
i1=0.53 となります。はい目出度し。
しかし、この場合は電圧計算が少しややこしくなるので、もう少し大胆にいきましょう。
9Ωのみを取払うのではなく、8Vの電源ごと取払ってしまえば、実にシンプルに考えることができます。この場合は等価回路2になります。結果はもちろん同じです。
こっちのほうがエレガントですね。テブナンの定理は柔軟に扱うのが肝要かと。
関連記事:テブナンの定理 と 重ね合わせの理 ① 2011-01-08
【重ね合わせの理】
テブナンの定理を使うことで電気回路の計算がずいぶん楽になりましたが、もうひとつ「重ね合わせの理」という妙手があります。やってみましょう。
左上の図が元回路です。これを中の図、下の図のように片方の電源を短絡して各電流を求めてみます。
8Vの電源から流れる電流は
i1a=8/(9+15/8) =0.74
i2a=0.74×3/8 =0.28 → -0.28(i2に対して逆)
i3a=0.74-0.28 =0.46
6Vの電源から流れる電流は
i2b=6/(5+27/12) =0.83
i1b=0.83×3/12 =0.21 → -0.21(i1に対して逆)
i3b=0.83-0.21 =0.62
そして、電流aと電流bを足します。この重ねあわせに“理”があります。
i1=i1a+i1b =0.74-0.21 =0.53
i2=i2a+i2b =-0.28+0.83 =0.55
i3=i3a+i3b =0.46+0.62 =1.08
となって、キルヒホッフで求めた各電流と一致しましたね。
何か狐につままれたような感じですが、これが「重ね合わせの理」です。
すごいっすね。(^^)
[テブナンの定理の補足]
右列の図を見てください。テブナンの定理を使って、9Ωに流れる電流i1を求めてみましょう。
ルールに沿って9Ωを取払い、まずa-b間電圧を求めます。これは8Vが直列に入るので少しややこしいですが、a-G間電を求めて8Vを引けばa-b間電圧になりますね。OKですか?(^^)
V(a-b)=6×(3/8)-8
V(a-b)=2.25-8 =-5.75
端子a-bから見た回路インピーダンスは5Ωと3Ωの並列ですから、
Ri=15/8 =1.88Ω
よって、元の回路は等価回路1に置き換えられます。
故に、 i1=-5.75/(1.88+9) よって
i1=-0.53
マイナスが付いているのは、電流がb→aに流れているということです。よって
i1=0.53 となります。はい目出度し。
しかし、この場合は電圧計算が少しややこしくなるので、もう少し大胆にいきましょう。
9Ωのみを取払うのではなく、8Vの電源ごと取払ってしまえば、実にシンプルに考えることができます。この場合は等価回路2になります。結果はもちろん同じです。
こっちのほうがエレガントですね。テブナンの定理は柔軟に扱うのが肝要かと。
関連記事:テブナンの定理 と 重ね合わせの理 ① 2011-01-08


























そうですね、正式には、「鳳・テブナンの定理」といいますね。鳳秀太郎という人が交流電源でも成り立つことを証明したとWikipediaに書いてありました。ほう?テブナンの定理、覚えやすい名称ですよね。
(^^)
実は私は、この「テブナン」と「重ね合わせの理」はそれほど懐かしいものではないんです。電気回路網は長年「キルヒホッフ」であくせくと解いていました。大学も文系だったものですから、就職してから非常~に後悔しましたね。この世界には私も趣味の延長から入りました。オーディオパワーアンプを自作するのが夢だったんです。