現在のナンプレ世界一難しい問題を、U字型磁石の原則(キタムラ)で解きます。
ご覧になる前に「ユニット」「磁石」「鉄」「同居」「別居=同居しない」「三回同居」「一回同居」
「同種」「異種」「磁石候補」「磁石相手候補」などの用語の意味を覚えておいてください。
解き易くします。
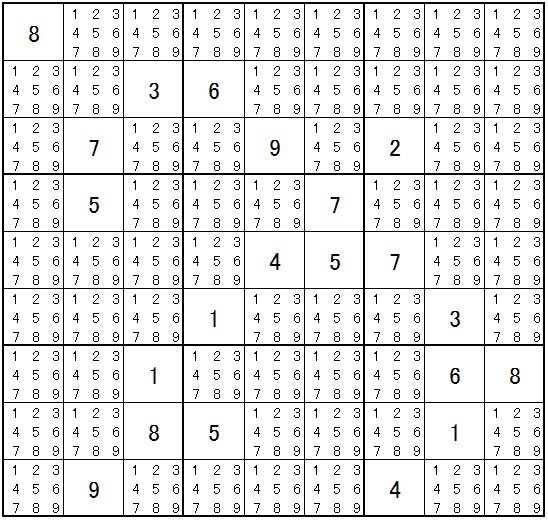
行・列・ブロックを整理して、

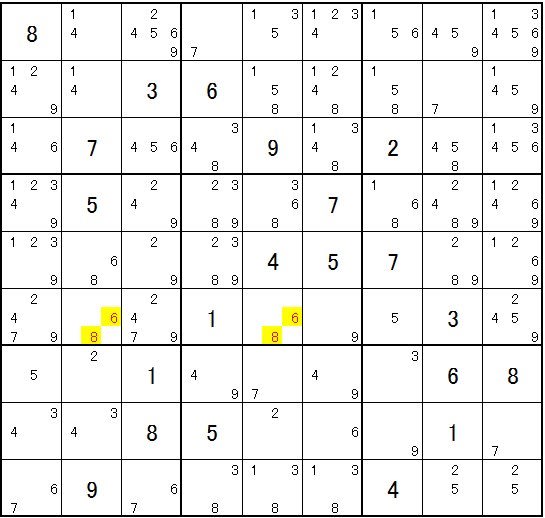
下段ユニットに注目してください。

1と8は一回のみ同居します。この場合1と8は磁石と鉄の関係になります。1の磁石候補は1-2,1-3、
1-7で、8の磁石候補は3-8,6-8になり、共通の磁石相手候補は3なので、3セルは1・3・8に確定
します。
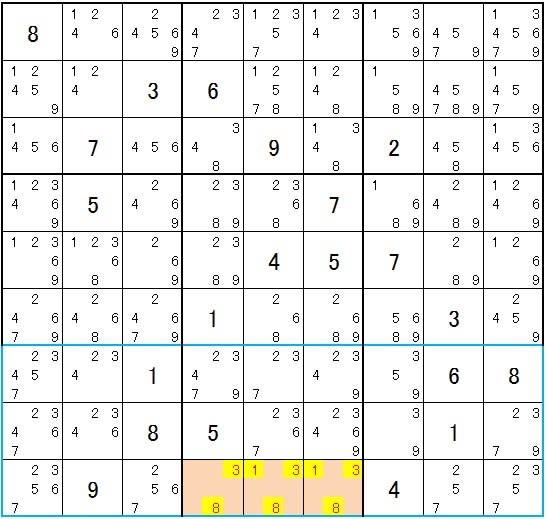
進めて

下段ユニット☐の7の磁石候補は7-2ですが、ここには5と6が入りますので磁石相手候補がいません。
従って、7は削除されます。

進めて

下段ユニット☐☐☐のルートの2-4は☐に5と6が入りますので磁石候補になりません。
☐にで5を削除すると1-3の磁石が確定してしまいます。作業中のユニットでそのユニットに直ちに磁
石を確定させてはいけないのです。磁石候補を絞る作業をします。なぜなら8-3も磁石候補だからです。
従って、5が入ります。
これから先はユニットで直ちに磁石を確定させるのでは無く、磁石候補を絞ることの証明を兼ねています。

進めて、

二国同盟で、

進めて、

中側ユニットで5は9と同居すると☐☐☐三回同居で5-9の磁石になり、絶対に同居しない6と同種に
なります。6は☐で9と同居すると☐で5が一回同居ですので、やはり5と6は同種になります。
同種は同居しないので6は削除されます。

進めて、

さらに進めて、

左側ユニット☐で5と8は一回同居で自社l区と鉄です。共通の磁石相手候補は6ですので6が入ります。

進めて、
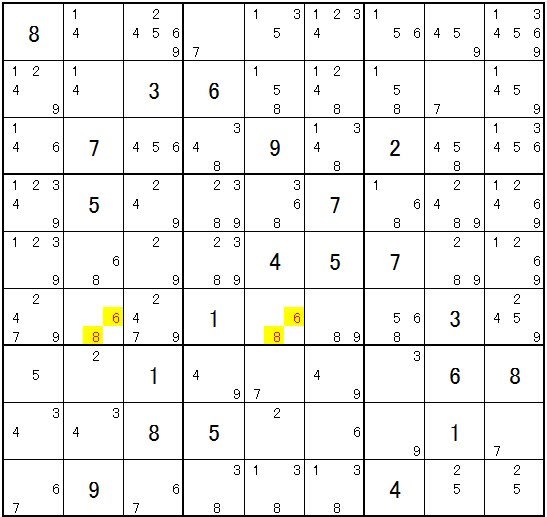
二国同盟で、
進めて、

二国同盟で、

進めて、

さらに進めて、

三国同盟で、

進めて、

さらに進めて、

どんどん数字が決まります。

正解です。
行った作業は9工程です。
① 1と3と8の同居を決めて。② 磁石相手候補のいない7を消して。③ 5と8の同種を決めて。
④ 二国同盟を使用して。 ⑤ 5と6の同種を決めて。 ⑥ 5と6と8の同居を決めて。
⑦ 二国同盟を使用して。 ⑧ 二国同盟を使用して。 ⑨ 三国同盟を使用しました。
2と3と8の三国同盟は解説のため、途中下車しただけです。
実際には1と4の二国同盟からノンストップでした。
ご覧の方も問題図を写してご自分で数字を消してみてください。
終わりの46連チャンに驚かれるかも知れません。
ご覧頂きましてありがとうございました。




















いろいろ実例を試しつつ会得したいと思ってます。その際 いろいろご意見いただければ有難いです。よろしくお願いします。
この記事はU字型に気が付いた当初のものです。
従って、何かぎこちない感じがすると思います。
貴殿の解き方は流石に奥が深いです。参考にさせて頂きます。
私はそこまで突っ込めません。
これからも色々教えてください。
1のペア候補は237、
8のペア候補は36、
共通のペア候補は3のみで、
最下行中央3セルは138に確定。
お見事!
この記事を参考に 背理法で解く方法をまとめてみました。
8a・|・・・|・・・
・b3|6・・|・・・
・7・|g9・|2・・
---+---+---
・5・|・・7|・・・
・c・|・45|7・・
・d・|1・・|・3・
---+---+---
・e1|・・・|・68
・f8|5・・|・1・
・9・|hij|4・k
abどちらかに24どちらかが入ります。
∵
abどちらにも24が入らないとすると ab16となり、
これは 基本手順だけで矛盾を確認できます。
efどちらかに24どちらかが入ります。
∵
efどちらにも24が入らないとすると ef36となり、
すると hij168から h8で gは34どちらか となりますが、
どちらの場合も 基本手順だけで矛盾を確認できます。
これで cdに24が入らないことがわかります。
すると dは68どちらかとなりますが、
d6とすると 基本手順だけで矛盾を確認でき、
d8とわかります。
また efには24のほかには36どちらかが入りますが、
f6とすると 基本手順だけで矛盾を確認でき、
efに入るのは3とわかります。
またここで k3とすると 基本手順だけで矛盾を確認でき、
hijが138の3国同盟になるととわかります。
(★ 最下行中央3セルは138に確定する との知見の活用です ★)
(★ これは なかなか気が付きません ★)
すると cは16どちらかなのですが、
c1とすると 基本手順だけで矛盾を確認できるようになり、
c6とわかります。
(★ 最下行中央3セルの3国同盟の効果です ★)
ここまでをまとめると、
c6 d8で kに3が入らない となりますが、
するとこのあとは 基本手順だけで最後まで解けます。
(★ 終わりの連チャン - たしかに驚きです ★)