私は独学でナンプレを解いてきました。「n国同盟」も「四辺形の原則」も「NISHIO LOGIC」も自分で見つけました。唯一「奇数(偶数)個連鎖」は勉強しましたが。それ故私の解き順に難しいロジックは有りません。ただ、「二択だけが残ると大きな一本の環になる」と信じていたことが恥ずかしいです。質問箱の回答に「XY-Chain」の記述を見て、目からウロコでした。早速訂正の記事を投稿させて頂きました「原則の根幹」です。これを覚えてからは二択を追うのが楽しくなりました。
ご覧の方も「n国同盟」「奇数個連鎖」「XY-Chain」の三つをマスターするだけで、実力は相当上がると思いますよ。それと「KITAMURA」も。
閑話休題、夏休みの宿題に次の図が出されました。
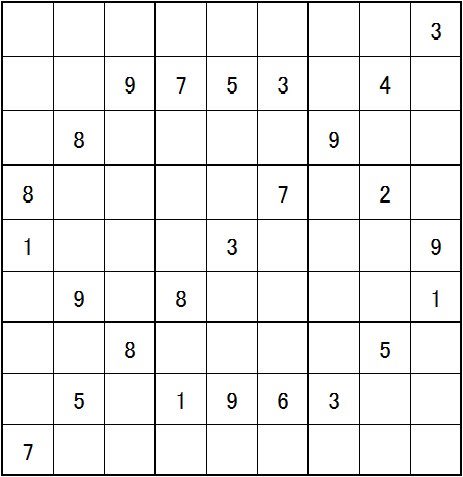
回答された方の説明を先に記します。

回答者の解説ーー「n国同盟と基本的な作業で上の図まで進みます。ここで Type3 Unique Rectangle というパターンを読み取って、7を削除する。」というものでした。私も不勉強なもので、Unique Rectangle を調べました。簡単に云うと「一解の原則」の応用編でType1からType4まで有るようです。間違った手法ではないようですが、「唯一解前提の手筋」として、あまり好まれてはいないそうです。ただ、タイムレースには非常に有効な手段とのことです。私の解き順には、この場面は出て来ませんのでご参考まで。

進めて、

さらに進めて、

上段ユニットで、5は☐で4と同居しないので、5と4は同種です。また、☐で5は3と一回同居で、5と3は異種です。しかしこれはどちらかは誤りです。どちらが誤りとしても、4と3は同種になります。同種は同居しませんので、4は削除されます。

進めて、
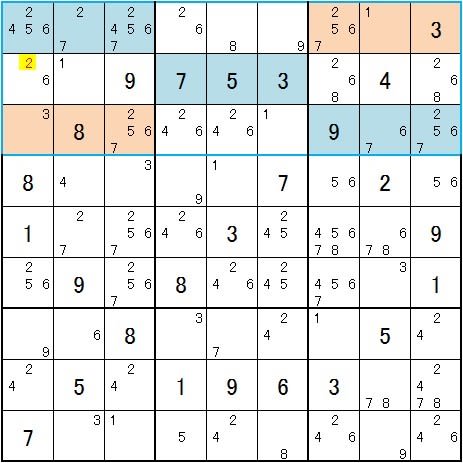
5は☐で2と同居しないので、5と2は同種です。また、☐で5は9と一回同居で、5と9は異種です。しかしこれはどちらかは誤りです。どちらが誤りとしても、2と9は同種になります。同種は同居しませんので、2は削除されます。

進めて、

5は☐で7と一回同居なので、5と7は異種です。また、☐で5は9と一回同居で、5と9は異種です。しかしこれはどちらかは誤りです。どちらが誤りとしても、7と9は異種になります。異種は一回同居ですので、7が入ります。

二国同盟で、

二国同盟で、

進めて、

二国同盟で、

進めて、

二国同盟で、

進めて、

さらに進めて、

残るは左側ユニットのみです。

正解です。
今回は少し緩めの題材にしました。しかし初心者の宿題にしては難しすぎると思います。
余談ですが、第2図の場面になった場合の、私の解き方を記します。
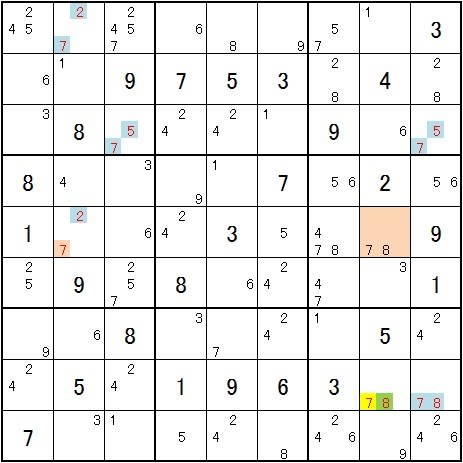
XY-Chainです。 7・8-8・7-7・5-5・7-7・2-2・7で☐の7は削除されます。
再度申し上げます。「n国同盟」「奇数個連鎖」「XY-Chain」の三つをマスターしてください。特に「奇数個連鎖」は強と弱の順番によって、確定する箇所と削除する箇所が違います。いろいろなパターンを覚えてください。
次回も質問箱からです。簡単なような、難しいような面白い問題です。

私はこの作品に「三手詰め」という名前を付けました。覚えて下さいと挙げたロジックだけで解けます。何日かけても宜しいのです。あれこれ考えるだけで実力は必ず上がります。是非挑戦してみてください。
ご覧頂きまして有り難うございました。









