下の図のような、1辺1cmの立方体4個を、立方体の四隅が重なるように貼り合わせて作った立体がある。この立体に1辺1cmの立方体を1個加え、同じように貼り合わせ、立方体5個からなる立体を作るとき、できる立体の種類として、最も妥当なのはどれか。ただし、回転させ、一致するものは1種類とみなす。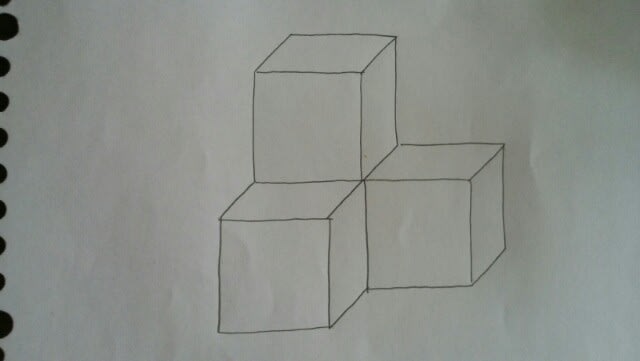 ①5種類②6種類③7種類④8種類⑤9種類
①5種類②6種類③7種類④8種類⑤9種類 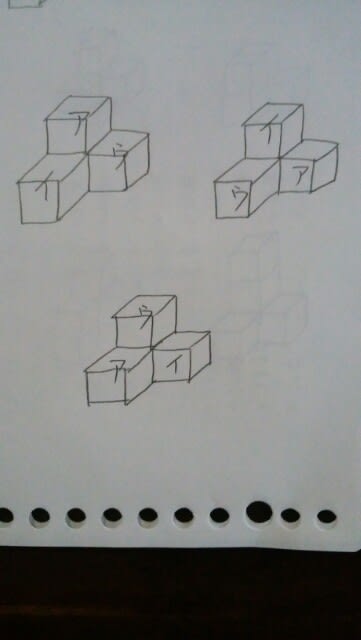 アが上にあると考えても、イが上だと考えても、ウが上だと考えても同じことです。よって、今、アが上だとします。そして、下の段に次のように立方体を加えてみます。
アが上にあると考えても、イが上だと考えても、ウが上だと考えても同じことです。よって、今、アが上だとします。そして、下の段に次のように立方体を加えてみます。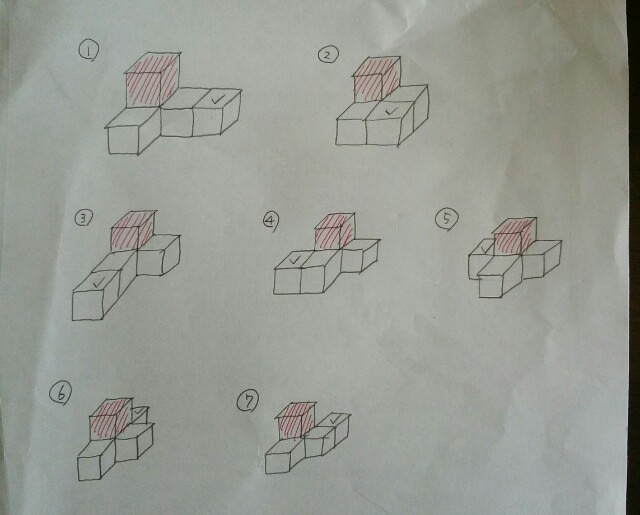 ⑤と⑥が同じ立体だということは、明らか。①と③も、同じ立体です。
⑤と⑥が同じ立体だということは、明らか。①と③も、同じ立体です。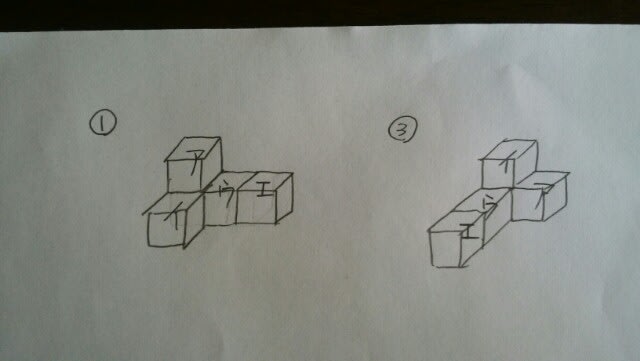 ④と⑦は、似ていますが、違う立体です。よって、5種類。実は、もうこれで、全て調べたことになります。
④と⑦は、似ていますが、違う立体です。よって、5種類。実は、もうこれで、全て調べたことになります。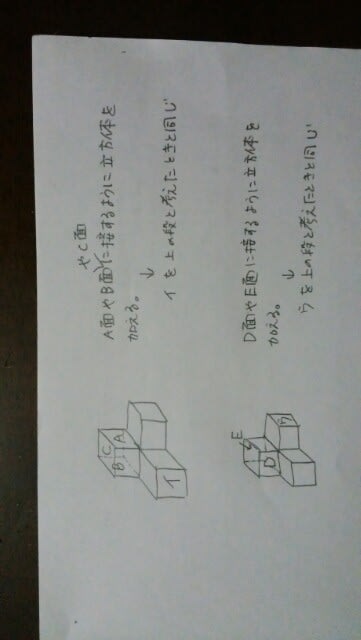
 結局、次の5種類です。
結局、次の5種類です。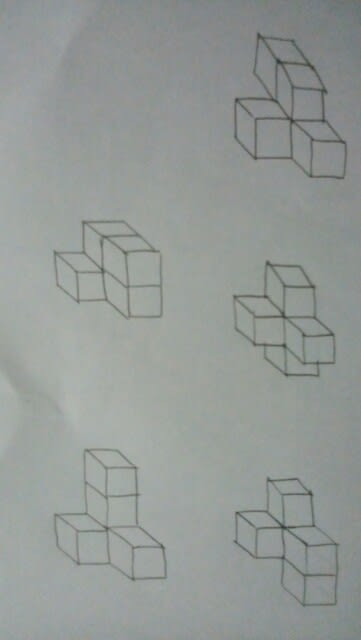 正解は、肢①です。
正解は、肢①です。

 ①5種類②6種類③7種類④8種類⑤9種類
①5種類②6種類③7種類④8種類⑤9種類  アが上にあると考えても、イが上だと考えても、ウが上だと考えても同じことです。よって、今、アが上だとします。そして、下の段に次のように立方体を加えてみます。
アが上にあると考えても、イが上だと考えても、ウが上だと考えても同じことです。よって、今、アが上だとします。そして、下の段に次のように立方体を加えてみます。 ⑤と⑥が同じ立体だということは、明らか。①と③も、同じ立体です。
⑤と⑥が同じ立体だということは、明らか。①と③も、同じ立体です。 ④と⑦は、似ていますが、違う立体です。よって、5種類。実は、もうこれで、全て調べたことになります。
④と⑦は、似ていますが、違う立体です。よって、5種類。実は、もうこれで、全て調べたことになります。
 結局、次の5種類です。
結局、次の5種類です。 正解は、肢①です。
正解は、肢①です。

ある法則に従うと、暗号の(0、4)(0、0)(3、3)(3、2)(4、4)(2、3)(3、4)(0、4)(0、0)が“AMSTERDAM(アムステルダム)”を意味する。このとき、(1、4)(2、3)(0、4)(3、3)(4、0)(1、0)(4、0)(0、4)が表す都市が首都である国として、最も妥当なのはどれか。 ①ドイツ②イラク③ブラジル④ベルギー⑤アルゼンチン 答えは、アルファベット8文字の都市が首都である国だから、実は、③が正解だと分かってしまいます。Berlin(6文字)、Baghdad(7文字)、Brasilia(8文字)、Brussel(7文字)、Buenos Aires(11文字)。この暗号は、パターン問題で、何度か解いたことがあったのではないでしょうか。0から4の数字を2つ組み合わせると、5(通り)×5(通り)=25(通り)。そして、アルファベットは26文字。最後のZだけは特別な記号にしたり、使わなかったりすれば、暗号として使えます。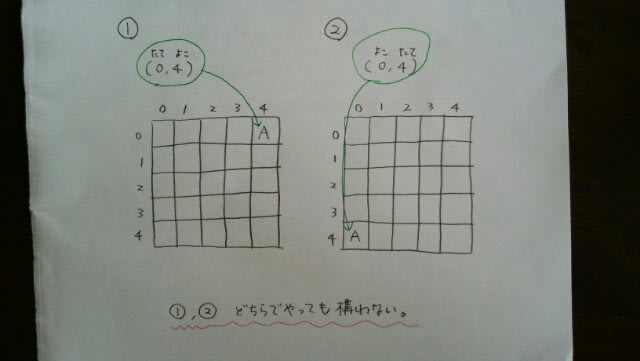 例えば、①でやってみると、
例えば、①でやってみると、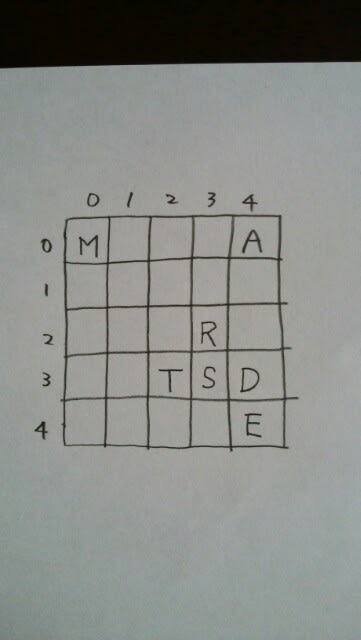 次に、配列を予想する。
次に、配列を予想する。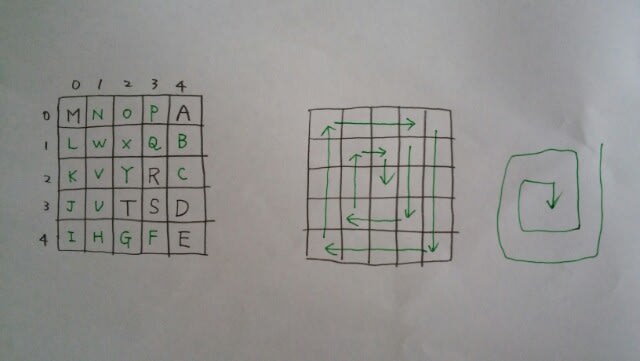 変換すると、
変換すると、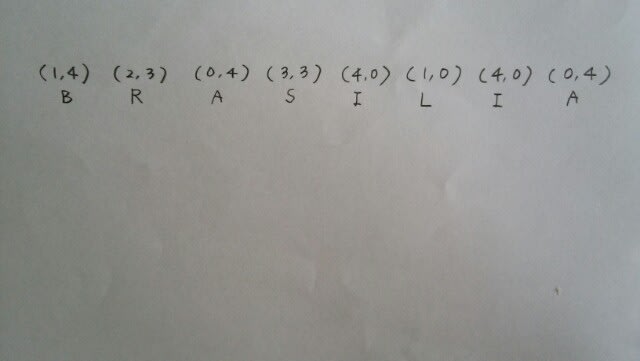 正解は、やはり③です。
正解は、やはり③です。

 例えば、①でやってみると、
例えば、①でやってみると、 次に、配列を予想する。
次に、配列を予想する。 変換すると、
変換すると、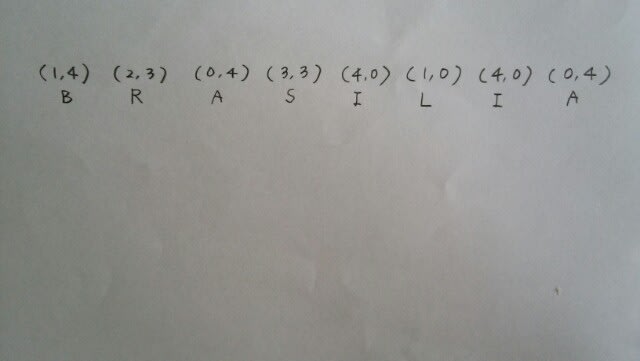 正解は、やはり③です。
正解は、やはり③です。











 正解は、④です。
正解は、④です。
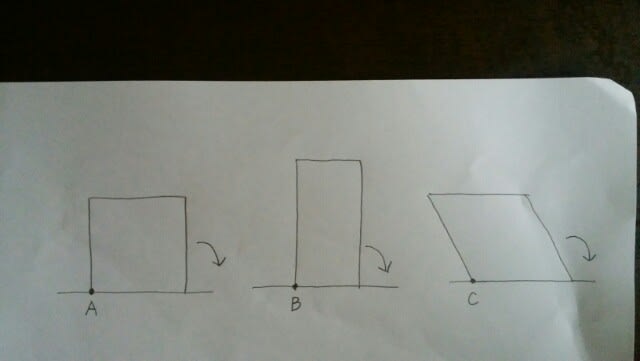

 軌跡の、基本問題です。正方形と、長方形は、いつでも90º回転なので、アは、Cの軌跡であることは、すぐに分かります。
軌跡の、基本問題です。正方形と、長方形は、いつでも90º回転なので、アは、Cの軌跡であることは、すぐに分かります。
 イとウは、半径の長さが、見分けるポイントです。
イとウは、半径の長さが、見分けるポイントです。
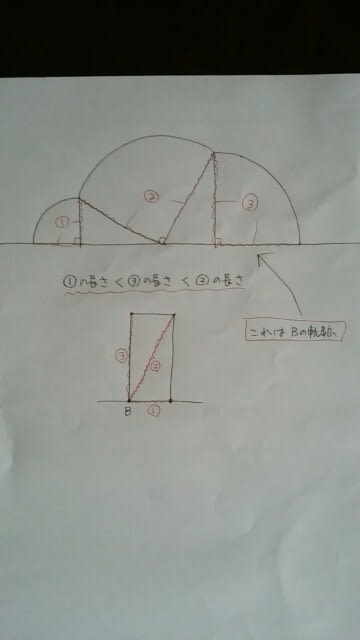 正解は肢4です。正方形が転がるときには、正方形の頂点の軌跡は、イのように、ドーム球場を正面から見たような形になります。
正解は肢4です。正方形が転がるときには、正方形の頂点の軌跡は、イのように、ドーム球場を正面から見たような形になります。


 よって、4+3+2=9(色)となり、正解は、③でした。
よって、4+3+2=9(色)となり、正解は、③でした。