見た目は全く同じコインが50枚ある。この中に1枚だけ他より軽いコインが混ざっていて、残りの49枚は同じ重さである。1台の天秤ばかりを使って、確実に軽いコインを見つけるための最少の回数として、最も妥当なのはどれか。ただし、偶然に見つけた回数は最少とはしないものとする。①3回②4回③5回④6回⑤7回 公式問題で、20年ほど前にはよく出題されていましたが、その後、姿を消し、3、4年前に、国家一般だったか、地上だったかで久しぶりに登場。それからまた最近ちらほらというやつです。2パターンあるので、区別して覚えて下さい。 本問は、1枚だけ軽いということが分かっているので、
本問は、1枚だけ軽いということが分かっているので、 正解は②です。なお、後の方の公式は覚えにくいので、重いか軽いか分かっていないときには、とりあえず、前の公式を使って何回かを求めて、それに1を足すと、ほとんど正解になります。(もちろん、きちんと公式に当てはめる方が良いのですが)また、この公式は、1枚だけ他と重さが違うときにだけしか使えないので、2枚以上のときは、公式は使いません。
正解は②です。なお、後の方の公式は覚えにくいので、重いか軽いか分かっていないときには、とりあえず、前の公式を使って何回かを求めて、それに1を足すと、ほとんど正解になります。(もちろん、きちんと公式に当てはめる方が良いのですが)また、この公式は、1枚だけ他と重さが違うときにだけしか使えないので、2枚以上のときは、公式は使いません。

 本問は、1枚だけ軽いということが分かっているので、
本問は、1枚だけ軽いということが分かっているので、 正解は②です。なお、後の方の公式は覚えにくいので、重いか軽いか分かっていないときには、とりあえず、前の公式を使って何回かを求めて、それに1を足すと、ほとんど正解になります。(もちろん、きちんと公式に当てはめる方が良いのですが)また、この公式は、1枚だけ他と重さが違うときにだけしか使えないので、2枚以上のときは、公式は使いません。
正解は②です。なお、後の方の公式は覚えにくいので、重いか軽いか分かっていないときには、とりあえず、前の公式を使って何回かを求めて、それに1を足すと、ほとんど正解になります。(もちろん、きちんと公式に当てはめる方が良いのですが)また、この公式は、1枚だけ他と重さが違うときにだけしか使えないので、2枚以上のときは、公式は使いません。

A~Eの5人が、それぞれ飼育しているイヌ、ネコ、トリ、カメ、メダカのペットについて、次のように発言している。5人の発言の内容の半分は本当で、残りの半分は誤りであるとき、確実にいえることとして、最も妥当なのはどれか。ただし、同じペットを飼育している者はいないものとする。 ①Aはカメを飼っている。②Bはトリを飼っている。③Cはネコを飼っている。④Dはメダカを飼っている。⑤Eはイヌを飼っている。 半分本当、半分ウソの、非常によくでるパターン問題でした。例えば、A=ネコとメモした場合、「Aが飼っているのはネコだ」という意味と、「ネコを飼っているのは、誰かというと、それはAだ」という、2つの意味があります。
①Aはカメを飼っている。②Bはトリを飼っている。③Cはネコを飼っている。④Dはメダカを飼っている。⑤Eはイヌを飼っている。 半分本当、半分ウソの、非常によくでるパターン問題でした。例えば、A=ネコとメモした場合、「Aが飼っているのはネコだ」という意味と、「ネコを飼っているのは、誰かというと、それはAだ」という、2つの意味があります。
 このように、Aの発言の前半が本当で、後半が誤りだったら、矛盾します。よって、Aの発言は、前半が誤りで、後半が本当だったのです。
このように、Aの発言の前半が本当で、後半が誤りだったら、矛盾します。よって、Aの発言は、前半が誤りで、後半が本当だったのです。 まとめてみると、Aはイヌ。Bはカメ。Dはトリ。Eはメダカだから、Cは残ったネコです。よって、正解は③です。
まとめてみると、Aはイヌ。Bはカメ。Dはトリ。Eはメダカだから、Cは残ったネコです。よって、正解は③です。

 ①Aはカメを飼っている。②Bはトリを飼っている。③Cはネコを飼っている。④Dはメダカを飼っている。⑤Eはイヌを飼っている。 半分本当、半分ウソの、非常によくでるパターン問題でした。例えば、A=ネコとメモした場合、「Aが飼っているのはネコだ」という意味と、「ネコを飼っているのは、誰かというと、それはAだ」という、2つの意味があります。
①Aはカメを飼っている。②Bはトリを飼っている。③Cはネコを飼っている。④Dはメダカを飼っている。⑤Eはイヌを飼っている。 半分本当、半分ウソの、非常によくでるパターン問題でした。例えば、A=ネコとメモした場合、「Aが飼っているのはネコだ」という意味と、「ネコを飼っているのは、誰かというと、それはAだ」という、2つの意味があります。
 このように、Aの発言の前半が本当で、後半が誤りだったら、矛盾します。よって、Aの発言は、前半が誤りで、後半が本当だったのです。
このように、Aの発言の前半が本当で、後半が誤りだったら、矛盾します。よって、Aの発言は、前半が誤りで、後半が本当だったのです。 まとめてみると、Aはイヌ。Bはカメ。Dはトリ。Eはメダカだから、Cは残ったネコです。よって、正解は③です。
まとめてみると、Aはイヌ。Bはカメ。Dはトリ。Eはメダカだから、Cは残ったネコです。よって、正解は③です。











 解法①選択肢を使う。
解法①選択肢を使う。 解法②普通に考える。
解法②普通に考える。

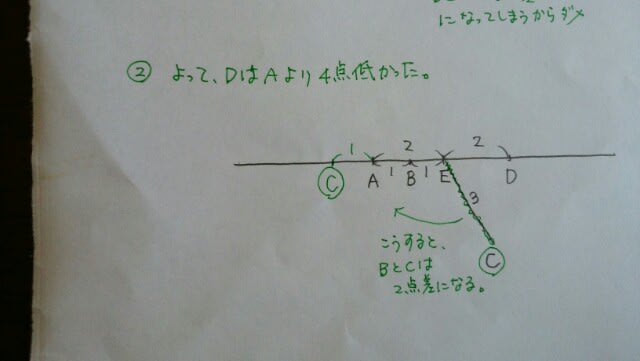 正解は肢4です。
正解は肢4です。