2021年地方上級の第5問は、仕事算と速さの融合問題でした。 ある家では、タマとムギという2匹の猫を飼っており、同じ量の餌を、毎朝、それぞれお皿に入れて与えている。タマは6分で食べきり、ムギは10分で食べきる。ある朝、ムギに餌をあげてから2分後、タマにも餌をあげたとき、お皿に残っている餌の量が同じになるのは、タマに餌をあげてから何分後か。 ただし、2匹とも、自分のお皿の餌しか食べないこととし、餌がなくなるまでそれぞれが食べる速さを変えずに食べ続けるものとする。(選択肢省略) 前半は仕事算ですね。 このブログでは、仕事全体の量を1として考えるのではなく、仕事を終える時間の最小公倍数として考える解法を採用しています。 6と10の最小公倍数は30ですから、餌の量を30とします。 タマは、30の餌を6分で食べ切るので、1分で5食べる。 ムギは30の餌を10分で食べ切るので、1分で3食べる。 ここからは速さの問題ですね。 ある朝、ムギに餌を与えて、その2分後にタマに餌を与えました。 このとき、ムギはすでに3×2=6だけ食べています。 ここまでを図にしておきます。
さあ、早食い競争が始まります。 ムギは現在6だけリードしていますが、なにせ、タマより食べるのが遅いので、やがてタマに追いつかれるのは必定です。 タマはムギよりも1分で2(5−3=2)だけ多く食べちゃいます。 ムギは、せっかく6だけリードしていても、毎分2ずつ差は縮まるので、3分後には追いつかれます。 このとき、こうなってます。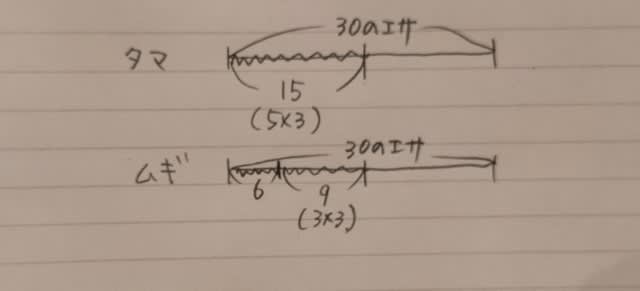
どちらにも同じ量の餌を与えたのだから、食べた量が同じになったということは、残った量も同じ。 本問は、「タマに餌をあげてから何分後か」と聞いているので、正解は3分後です。
おちゃメンタル☆パーティー 下谷あゆ


さあ、早食い競争が始まります。 ムギは現在6だけリードしていますが、なにせ、タマより食べるのが遅いので、やがてタマに追いつかれるのは必定です。 タマはムギよりも1分で2(5−3=2)だけ多く食べちゃいます。 ムギは、せっかく6だけリードしていても、毎分2ずつ差は縮まるので、3分後には追いつかれます。 このとき、こうなってます。

どちらにも同じ量の餌を与えたのだから、食べた量が同じになったということは、残った量も同じ。 本問は、「タマに餌をあげてから何分後か」と聞いているので、正解は3分後です。

おちゃメンタル☆パーティー 下谷あゆ










