あるイベントに集まった子ども全員にあめ玉を配る。1人に2個ずつ配ると30個余り、1人に6個ずつ配ると最後の1人には少なくとも1個は配れるが、6個は配ることができない。1人に5個ずつ配るとあめ玉は何個余るか。 ①2個②3個③4個④5個⑤6個 (解法1)まずは、ウォーミングアップから。例えば、あめ玉が40個あります。これを6人の子どもたちに7個ずつ配るとどうなるかというと、こうなりますね。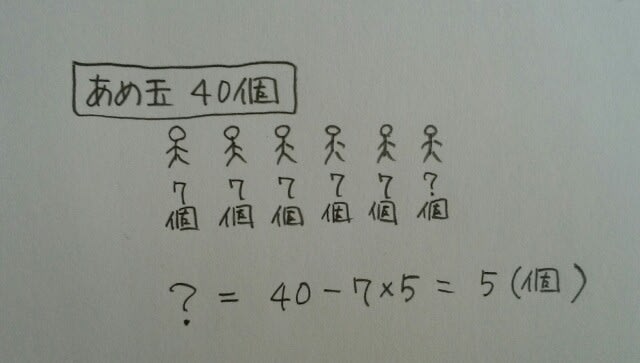 子どもの数をx人とすると、あめ玉は2x+30個あったことになります。6個ずつ配ったときに、最後の1人がもらえるあめ玉の個数を式で表すと、
子どもの数をx人とすると、あめ玉は2x+30個あったことになります。6個ずつ配ったときに、最後の1人がもらえるあめ玉の個数を式で表すと、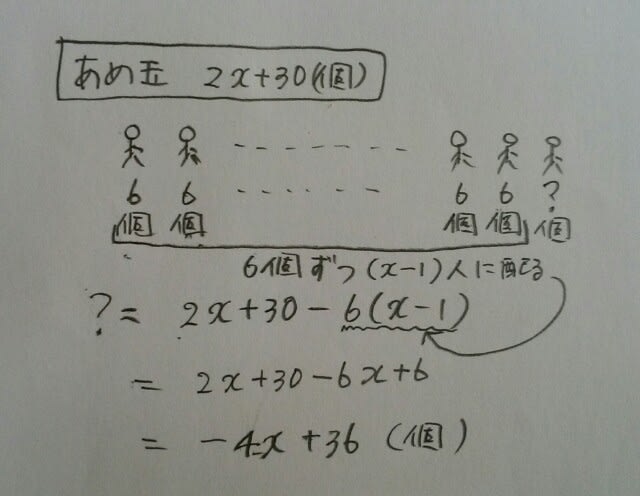 これが1個から5個の範囲だから、 1≦-4x+36≦5。これを解くと、
これが1個から5個の範囲だから、 1≦-4x+36≦5。これを解くと、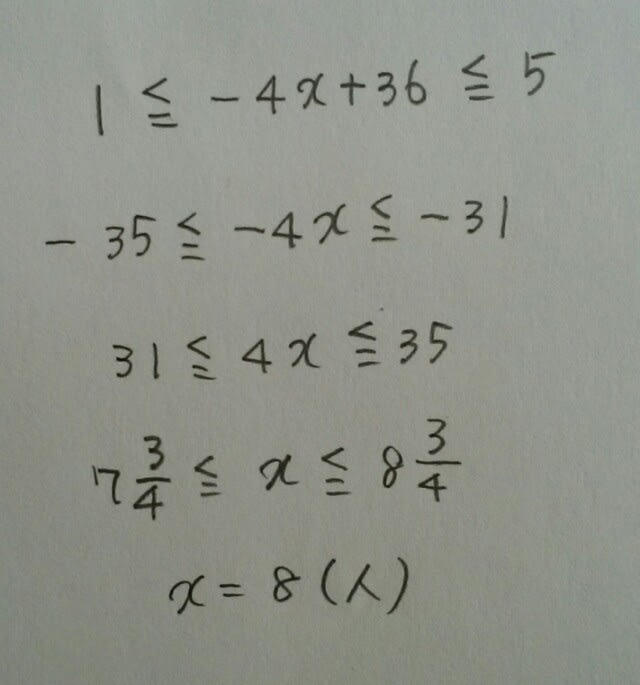 ってか、xが7だったら-4x+36は8になるし、xが8だったら-4x+36は4になるからOK!のほうが簡単です。 子供は8人で、あめ玉は2×8+30=46個です。46個のあめ玉を、8人に5個ずつ配ると、 46-5×8=6。6個余ります。正解は、肢⑤です。 (解法2)あめ玉が2x+30個あるところまでは同じです。このあと、最後の1人がm個もらうとします。すると、
ってか、xが7だったら-4x+36は8になるし、xが8だったら-4x+36は4になるからOK!のほうが簡単です。 子供は8人で、あめ玉は2×8+30=46個です。46個のあめ玉を、8人に5個ずつ配ると、 46-5×8=6。6個余ります。正解は、肢⑤です。 (解法2)あめ玉が2x+30個あるところまでは同じです。このあと、最後の1人がm個もらうとします。すると、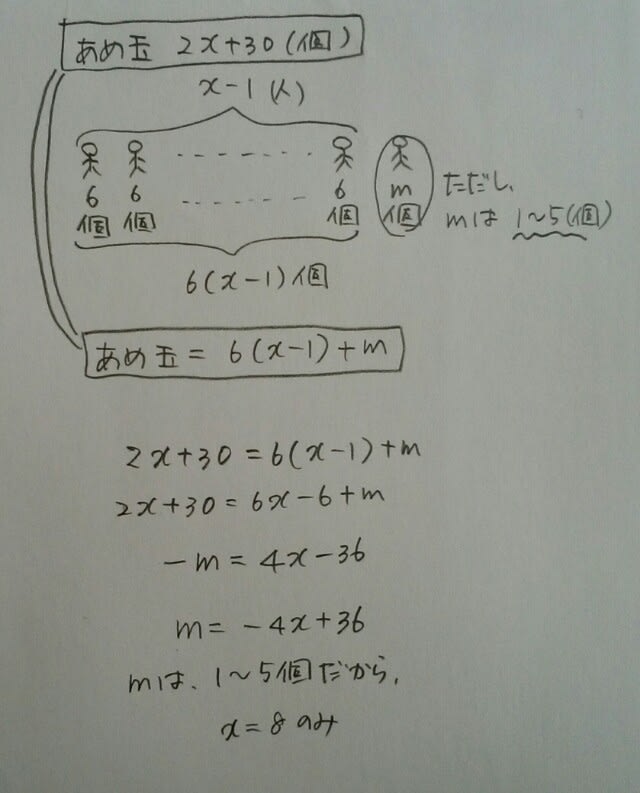 以下、解法1と同じです。不等式にすると、どうも失敗が多くなるなあという人は、解法2を試してみてね。ここをポチッとお願いします。→
以下、解法1と同じです。不等式にすると、どうも失敗が多くなるなあという人は、解法2を試してみてね。ここをポチッとお願いします。→
にほんブログ村

 子どもの数をx人とすると、あめ玉は2x+30個あったことになります。6個ずつ配ったときに、最後の1人がもらえるあめ玉の個数を式で表すと、
子どもの数をx人とすると、あめ玉は2x+30個あったことになります。6個ずつ配ったときに、最後の1人がもらえるあめ玉の個数を式で表すと、 これが1個から5個の範囲だから、 1≦-4x+36≦5。これを解くと、
これが1個から5個の範囲だから、 1≦-4x+36≦5。これを解くと、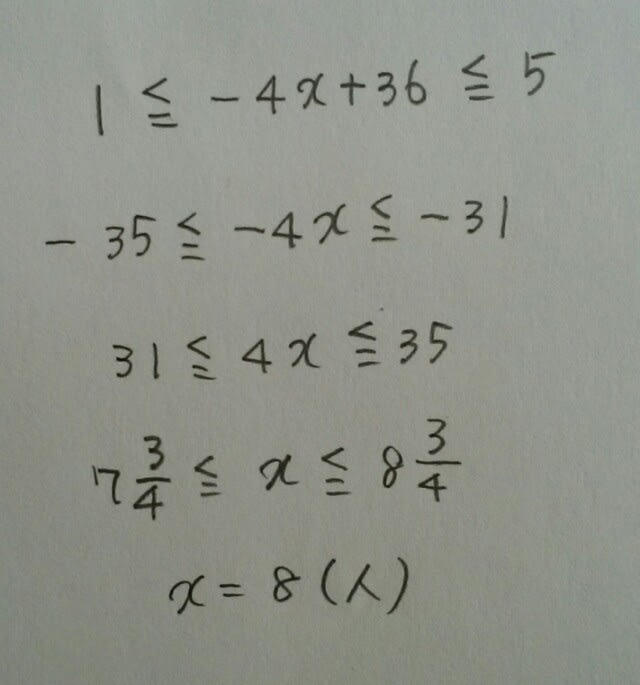 ってか、xが7だったら-4x+36は8になるし、xが8だったら-4x+36は4になるからOK!のほうが簡単です。 子供は8人で、あめ玉は2×8+30=46個です。46個のあめ玉を、8人に5個ずつ配ると、 46-5×8=6。6個余ります。正解は、肢⑤です。 (解法2)あめ玉が2x+30個あるところまでは同じです。このあと、最後の1人がm個もらうとします。すると、
ってか、xが7だったら-4x+36は8になるし、xが8だったら-4x+36は4になるからOK!のほうが簡単です。 子供は8人で、あめ玉は2×8+30=46個です。46個のあめ玉を、8人に5個ずつ配ると、 46-5×8=6。6個余ります。正解は、肢⑤です。 (解法2)あめ玉が2x+30個あるところまでは同じです。このあと、最後の1人がm個もらうとします。すると、 以下、解法1と同じです。不等式にすると、どうも失敗が多くなるなあという人は、解法2を試してみてね。ここをポチッとお願いします。→
以下、解法1と同じです。不等式にすると、どうも失敗が多くなるなあという人は、解法2を試してみてね。ここをポチッとお願いします。→にほんブログ村











