微分（加速度、速度、距離）

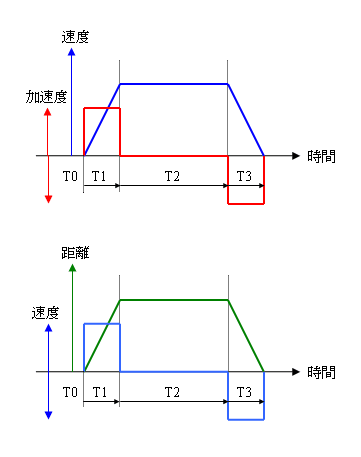
お父さんはT1の期間アクセルをめいっぱい踏みました。プラス加速度が一定値となり車はどんどん速度を上げていきます。ふと前方にパトカーを発見したためT2ではアクセルを戻し加速度はゼロとなり、車は等速走行となりました。目的地が見えたので、お父さんはブレーキを踏みT3ではマイナス加速度が一定値となり車はしだいに減速しT3後車は無事目的地に到着しました。

さて、距離を微分すると速度、速度を微分すると加速度、加速度を積分すると速度、速度を積分すると距離です。

時間と共に変化するある物理量の微分値は、変化の増減値として表れます。増がプラス、減がマイナス、変化が無ければ増減値はゼロです。図の速度と加速度の関係を見ると、T1において速度は増加を続け、増分（微分値）としてプラス側に表れているのが加速度です。速度が直線的に増加しているので、時間当たりの増分は一定ですから、T1において加速度は一定値となっています。これはT1において加速度が一定値であるから、速度が直線的に増加するともいえます。

物体の落下運動もこれと同じです。重力加速度は9.8m/sec^2と固定値ですから、ある高さから物を落とせば、落下速度は時間と共に直線的に増加していきます。これを「等加速度運動」といいます。

T2を見てみましょう。速度は一定速度でありこの間は増加も減少もゼロですから、速度の微分値である加速度はゼロです。T3では減速していますので減少分として加速度はマイナスに表れています。これも直線的に減速していますので等加速度運動です。

関連記事：
微分（意味と約束事）2007-10-08
加速度の微分値は？ 2007-11-04