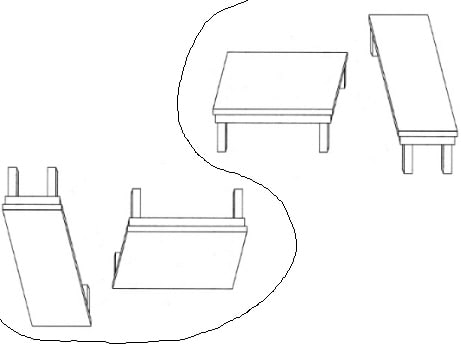
図の右上の二つのテーブルの天板は同じ形の平行四辺形です。
シェパードという心理学者の考案した錯視図ですが、二つの平行四辺形が同じ形、大きさだといわれても、とても信じられないのではないでしょうか。
実際測って見れば分かるのですが確かに同じ大きさの平行四辺形です。
これは遠近感による錯視だといわれていますが、いわゆる遠近法に従った図形ではありません。
どちらの天板も手前側より奥側のほうが広がって見えるのですから、普通の遠近法と逆です。
奥行き感があるのに、手前側と奥側が同じ長さに描かれているため、奥側が長く見えてしまうということなのです。
左下は右上の図を180度回転させたもので、つまり右上の図を逆さまに見たものです。
こうしてみると、二つの平行四辺形は左側のほうが細長く見えますが、右上の図の場合ほどではありません。
右上の場合は二つの平行四辺形の形はだいぶ違って見えたのですが、左下の図ではあまり違って見えません。
左下の場合は、それぞれの平行四辺形の四隅に注意を向けて見れば、ほぼ同じ形に見えてくるでしょう。
それだけでなく右上の場合はゆがんで見えた平行四辺形が、左下の場合はゆがみが少なく見えます。
同じ図であるのに右上の図と、左下の図では形が劇的に違ってしまっています。
その理由は奥行き感の違いです。
右上では感じられた奥行き感が、左下の場合はほとんど感じられないのです。
右上の図でのテーブルの縁や脚は線遠近法には従わない形で、絵画的に示されています。
このままなら少し違和感があっても、テーブルを立体的に描いたものと見るので、奥行き感が感じられます。
ところが180度回転した形で見るとテーブルの立体図としてはかなりの違和感があり、そのため脚のついているほうが特に手前に感じられるということがなく、奥行き感があまり感じられないのです。
その結果左下の図は平面的に見えてしまい、実際の姿である平行四辺形に見えてくるのです。
つまり逆さまのほうから見た場合は、ありのままの姿に近く見えているのです。
B.エドワーズ風にいえば右脳で見るからだということになるのでしょうが、逆さまにしたほうの図を模写すれば右上の図を模写するよりも忠実に描けるのは確かです。
そうすると右上の図は左脳で見ているということになってしまいそうですが、本当にそうでしょうか。
右上の図は絵画的に遠近感を表現したのですが、線遠近法に従っていないので、さかさまにした左下の図は絵画的な手がかりが力を失ってしまっているのです。
この例では逆さまにして見ることで錯視効果がなくなり、忠実に模写しやすくなるのですが、逆さまに見れば必ず錯視効果が解消されるというものではないからです。