差動増幅回路の妙④ フィードバック、オペアンプ

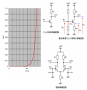
左上の回路が前回検討した回路です。14300ものゲインを持つじゃじゃ馬で、IN1に＋0.1Vを入力すれば出力は電源電圧の＋15Vに張り付き、－0.1Vを入力すれば出力は電源電圧の－15Vに張り付くというものでした。

それでは右の回路のように、1本の抵抗RF（9kΩ）を追加してOUTとIN2を接続するとどうなるでしょう（IN2はグランドから切離す）。端子を点線にしている1kΩはまだつなぎません。Q2のベース電流を無視量、つまり入力インピーダンス＝∞Ωとすると、OUTの電圧がaVだけ上昇すれば、IN2もまったく同じaV上昇します。つまり、OUTの電圧＝IN2の電圧になります。ここが重要なところですよ。OKですか？

そしてaVが、IN1＝0.1Vを超えると、IN1よりもIN2の電圧が高くなり、出力OUTは－15Vに向きを変えて瞬時に変化します。IN2の値は出力OUTと同じですから、次にOUTの電圧がIN1＝0.1Vを下回れば、OUTは再び＋15Vに向きを変えて瞬時に変化します。このようにOUTはIN1の電圧を境に、オーバーシュート、アンダーシュートを繰り返しますが、振動し続けるわけではありません。IN2の電圧がIN1の電圧を横切れば、出力OUTが必ず引き戻すように動作するので、“しばらく”するとIN2の電圧＝IN1の電圧＝0.1Vとなる地点でOUTは静止します。“しばらく”の期間は遅くてもμsecオーダーですから無視量として、瞬時にOUTは静止すると考えて問題ありません。つまり出力OUTを抵抗（今の場合は9kΩ）でIN2に接続すれば、IN1＝IN2＝OUT（＝0.1V）となるのです。OUTとIN2を抵抗（0Ωも可）で接続することをフィードバックするといいます。

つまりIN2の電圧＝IN1の電圧となる値にOUTは静止するということです。であるなら、いよいよ次が大詰めです。端子を点線にしている1kΩを接続するとどうなるでしょう。見てきたように、出力OUTはIN1＝IN2になる電圧で静止するのですから、OUTは9kΩと1kΩで分圧した値が0.1Vになるような値に決まります。つまり

0.1＝OUT×1k / 9k＋1k　1k＝OUT×1k　OUT＝1

このように、OUT＝1Vになります。入力はIN1＝0.1Vですから、ゲインは10ということですね。1kΩを3kΩに取り替えると、OUTは0.4Vとなり、ゲインは3になります。これは実際に計算してみてくださいね。先に結論をお話しますと、右の回路図で、あとに接続した1kΩをR1、フィードバック抵抗の9kΩをR2とすると、この増幅回路のゲインは

Gain＝1＋R2/ R1

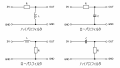
となります。最後に下の図をみてください。もうお気づきですね。これがオペアンプなのです。

関連記事：
差動増幅回路の妙③ 2段目とエミッタフォロワ 2011-04-27
差動増幅回路の妙① エミッタ接地増幅回路 2011-04-13

差動増幅回路の妙③ 2段目とエミッタフォロワ

さて、右の回路図は何でしょう。これは差動増幅回路の出力（OUT1）をQ3のエミッタ接地増幅回路でさらに増幅し、それに出力回路のエミッタフォロワを取り付けたものです。

2段目の増幅回路はバイアス電流を1mAとしましたのでコレクタ抵抗R4は14.3kΩになります。ゲインは143倍にしましょう。すると、Gain＝R4/R3で、エミッタ抵抗R3は100Ωと決まります。

さて、差動増幅回路はというと、エミッタ電流を1mAとするとエミッタ抵抗は14.3kΩ。IN1を信号入力とし、IN2は0Vに固定、OUT1を出力としています。Q1のR1は1.6kΩとしていますが、なぜ1.6kΩなのかは考えてみてください。IN1の入力に対してOUT1は極性が反転します。それがQ3の増幅回路に入力されるので再度反転し、結果的にIN1の入力とエミッタフォロワの出力OUTは同相になります。

回路全体のゲインはどれくらいでしょう。Q3の増幅回路はゲイン＝143ですね。差動増幅回路のゲインは、よくわかりませんが“非常に大きい”でした。まあ100くらいに考えておきましょう。すると回路全体のゲインは、100×143＝14300と、これはとてつもなく大きな値になります。さて、こんなものが使い物になるのでしょうか？実はゲインは大きければ大きいほど良いのです。これも最後にスッキリします。

試しに、IN1に⊿V＝0.1Vを入力してみましょう。そのまま計算すれば0.1×14300＝1430Vになりますが、回路図から明らかなように出力は電源電圧以上にはなり得ないので、出力（OUT）は＋15Vです。⊿V＝－0.1Vを入力すれば、同様に出力は－15Vです。

さて、どうしましょうか。

関連記事；
差動増幅回路の妙④ フィードバック、オペアンプ 2011-05-01
差動増幅回路の妙② 入出力とゲイン 2011-04-21

差動増幅回路の妙② 入出力とゲイン

差動増幅回路の妙① エミッタ接地増幅回路

図中の珍妙な回路は「差動増幅回路」といい、これが本稿の主題です。この差動増幅回路もエミッタ接地増幅回路の変形であり、誰が考えたのか、実におもしろい動作をします。回路の形も左右対称で分かりやすいので、ぜひこの形を覚えてください。電子回路は動作の中身を理解することと同じくらい、回路の形を覚えることが重要です。

この回路はエミッタ抵抗Reを共有する、2つのエミッタ接地増幅回路（電流帰還増幅回路）と見ることができますね。つまり図から明らかなように、この回路は入力と出力が2つずつあるということです。

さて、この回路はいったいどんな動作をするのでしょう。順を追ってみていきます。図に示されている条件において、まずエミッタ抵抗1kΩに1mAが流れていることが分かります。OKですか？ということは、トランジスタQ1のコレクタ電流Ic1と、トランジスタQ2のコレクタ電流Ic2は、共に0.5mAが流れています。（ベース電流は無視量として）。OKですね？ということは、OUT1（Q1のコレクタ電圧Vc1）とOUT2（Q2のコレクタ電圧Vc2）は同じ電圧値になっています。これが直流的（静的）に見た各値、すなわち各部の動作点です。

この状態で、IN1の電圧を⊿V上げたとします。するとQ1のVbeがわずかに増えてIc1が増加します。この時Ic1の増加分がRe（1kΩ）に流れてエミッタ電圧Veが増加するように思えますが、実はそうはなりません。Q1のVbeがわずかに増えればQ2のVbeはわずかに減少しますね。ということはQ2のIc2も減少します。つまりIc1が増えればIc2が減り、Ic1が減ればIc2が増えるという動作をするわけです。そして、Ic1＋Ic2は常に（ほぼ）1mAを保ちます。よってRe（1kΩ）には一定値の1mAが流れ続け、結果としてエミッタ電圧Veは、ほぼ一定の電圧値を保つことになります。

さてエミッタ電圧Veが一定ということは、Q1、Q2の増幅動作は、最初に見た「エミッタ接地増幅回路」と同じ、ということになります。（エミッタ接地増幅回路のエミッタはグランドに直結ですから、Ve＝0Vと一定です）。こうなると差動増幅回路のゲインは、電流帰還増幅回路でやったように、Rc/Reという具合に簡単に求めることはできません。再び最初に戻り、指数関数のグラフをにらみながら、Vbe-Ib特性を考えることになります。しかしまあ、それも面倒なのでやめにして、エミッタ接地増幅回路のゲインを思い出してください。「エミッタ接地増幅回路のゲインは非常に大きい」でしたね。差動増幅回路のゲインもこれと同じで、“非常に大きい”のです。×100くらいでしょうか、×1000くらいでしょうか、まあその程度に捉えておけばいいでしょう。”そんないい加減な”と思われるでしょうが安心してください。話しの最後に辻褄が合ってスッキリします。


次に入出力の関係を見てみます。信号電圧はIN1にもIN2にも入力できます。このとき出力電圧はOUT1からもOUT2からも取り出せます。OKですか？そしてIN1に入力した場合OUT1は逆相、OUT2は同相出力となり、IN2に入力した場合はOUT1が同相、OUT2が逆相出力となります。OKですね？では、IN1とIN2、両方に入力するとどうなるでしょう？

はい。ここで一旦、コーヒーブレイクにしましょう。（＾＾）

関連記事：差動増幅回路の妙③ 2段目とエミッタフォロワ 2011-04-27

差動増幅回路の妙① エミッタ接地増幅回路

トランジスタといえば、まず「増幅」を思い浮かべると思います。確かにトランジスタは電流増幅も電圧増幅もやってくれます。しかし基本は電流増幅であり、Ic（コレクタ電流）＝hFE×Ib（ベース電流）の関係が成り立つので、Ibを調整することによってIcを制御することができます。hFE（直流電流増幅率）はおおむね100程度と考えてください。

この関係式に沿い、Ib＝1mAとするとIc＝100mAであり、Ib＝3mAとするとIc＝300mAとなります。当然ですね。入力電流IbをhFE倍したものが出力電流Icとなる、つまりこれがトランジスタによる電流増幅の意味です。ここで1点、非常に重要な、トランジスタであるが故の性質があります。それはIcが「定電流」だということです。

Icが定電流であればこそ、負荷抵抗Rをコレクタに挿入し、Rによる電圧降下を出力電圧として取出すことができるのです。これを具体的に示しているのが図の「エミッタ接地増幅回路」です。この回路がトランジスタによる増幅回路の原型です。

これはINからIbを流し、hFE倍されたIcが負荷抵抗Rcを流れ、その電圧降下をOUT（Vc）としてコレクタから出力する回路です。

ではこのエミッタ接地増幅回路のゲイン（増幅倍率）はどれくらいでしょう。ゲインは「出力/入力」ですが、出力電圧Vcと入力電流Ibの割算は意味がありません。ゲインは「出力電流/入力電流」あるいは「出力電圧/入力電圧」でなければなりません。この入力電圧に相当するのがVbe（ベース・エミッタ間電圧）です。

そもそもIbも電圧源があるから流れるわけで、電流が単独で流れることはありません。よって、エミッタ接地増幅回路のゲインは「Vc/Vbe」となります。

さてこの先の話は少し難しくなります。また残念なことに、このエミッタ接地増幅回路はこのままでは実用として使い物にならないことが分かります。

NPNトランジスタのB-Eは、PN接合のダイオードと同じですね。左のグラフはダイオードのVf-If特性を、指数関数によってシミュレートしたものです。これをトランジスタのVbe-Ib特性に当てはめてみます。まずVbe＝0.7VとするとIb＝30mAですね。このVbe＝0.7Vを基準（動作点）として0.05V増加させるとIb＝70mA辺りになることが分かります。Vbeを0.1V増加させると、スケールオーバーしてもう読めません。

つまりVbeの動作点からの電圧変化に対して、Ibの変化は極めて大きいのです。Icに至ってはIbがhFE倍されるので、Vbeのわずかな変化によりとてつもなく大きな変化になります。これはエミッタ接地増幅回路のゲイン、すなわちVc/Vbeが非常に大きいことを意味し、そのこと自体は悪くないのですが、動作点としたVbe＝0.7Vが微動だにせず安定しているということは実際にはあり得ません。ミクロ的に見るといろんな要因がノイズになりVbeの動作点は微妙に変化し続けています。これではIc、あるいはVcの動作点は大きく変動してしまい（信号を入力していないのに、出力が勝手に変化する）、安定した増幅回路にはなりません。

もう1点、致命的な問題があります。実際のトランジスタはコレクタからベースにわずかな漏れ電流があるのです。この漏れ電流がIbを増加させ、それによりIcが増加し、その分さらに漏れ電流が増加し、またさらにIcが増加するという繰返し現象が発生し、最後にはトランジスタが過熱して破壊します。これをトランジスタの「熱暴走」といいます。

というわけで、図のエミッタ接地増幅回路は実用になりません。そこで、上述した様々な問題を修正して考案されたのが、右の「電流帰還（エミッタ接地）増幅回路」です。最大の改良点は1つ。“エミッタ抵抗Reを入れた”ことです。

さて、このReはどのような働きをするでしょう。動作点Vbe＝0.7Vの変動を考えてみます。Vbeがわずかに増加したとすると、Ibが増加しIcはそのhFE倍増加します。ここまでは同じです。しかしIe＝Ib＋Icですから、IbとIcの増加分は共にReに流れます。そうするとReの端子電圧がその分増加し、結果としてエミッタ電圧Veが増加します。すると、Vbe＝Vb－VeですからVbeが小さくなりますね。つまり、Vbeが無駄に大きくなろうとしても、ReによってVbeの増加を抑え込み元に戻してしまうのです。Vbeが無駄に小さくなろうとしても同じことです。これにより、Ib、Ic、Vc、すべての動作点が非常に安定します。“あっぱれ！Re”ってところですね。

少し脱線しますが、トランジスタは用途が大きく2つあります。①スイッチとして使う、もしくは、②増幅器として使う、このどちらかです。基板の現物や回路図からトランジスタがどちらの用途に使われているかを見分ける方法は、Reがあるかどうかです。Reのない増幅回路はあり得ないと思っていてもいいでしょう。スイッチとして使われている場合はエミッタがグランド（GND）に直結されています。

さて、Reを取り付けたことによる、大きなメリットはまだあります。ReがなければVbe-Ib特性は上述のように指数関数になりますから、特性が非常にクリティカルになりVbeの値からIbの値を知ることは、測定する以外にまず不可能です。しかしVbeはIbの値に関わらず、ほぼ0.7V近辺にいるわけですから、Vbe＝0.7Vと割り切れば、Reがある場合Ve＝Vb－0.7Vとなって、Ie＝Ve / Reとまずエミッタ電流が簡単に求まります。それから入力電圧：⊿Vb＝⊿VeでありIc≒Ieですから、ReとRcの電圧降下の比はRc/Reとなります。よって、結局この増幅回路のゲイン（⊿Vc/⊿Vb）は、ほぼRc/Reで決まるのです。これは嬉しいですね！最後にIbはIc / hFEで求まり、Ic＝1mA、hFE＝100とするとIb＝0.01mAとなります。非常に小さな電流値ですから、Ib＝0として扱っても大きな問題はないでしょう。

というように、Reを入れることにより、増幅回路に必要な各要素の計算が簡単にできてしまいます。いかがですか? もういちど、“あっぱれ！Re”。

さて、下のもうひとつの珍妙な図は「差動増幅回路」といい、これもエミッタ接地増幅回路の変形です。非常におもしろい動作をするのですが、これのお話はまた次回ということにしましょう。

関連記事：
差動増幅回路の妙② 入出力とゲイン 2011-04-21
オペアンプを作ろう① 定電圧回路 2010-05-18
定電圧電源を作ろう①ツェナ 2009-12-14

フィルタ回路④ ひっくり返せば逆フィルタ

ひっくり返せば逆フィルタ

RLハイパスフィルタのRLを入れ替えればローパスフィルタになります。同様に、RCローパスフィルタのRCを入れ替えればハイパスフィルタになります。

つまり、ハイパスもローパスもCRだけでできてしまうということです。実際、微少電流かつ低周波（目安として1MHz以下）でのフィルタ回路はほとんどCRで設計します。コンデンサは品種が多く、目的のフィルタ特性に応じてセレクトしやすいのも理由の一つです。

ということで、CRの共振周波数

ω0＝1/ CR　f0＝1/ (2πCR )

は非常に！重要な式なのです。何を忘れてもこれだけは覚えていること。これは肝に銘じていても損はありません。

関連記事：
フィルタ回路③ 微分回路と積分回路 2011-03-11
フィルタ回路① LRとCR 2011-03-03 00:31:41

フィルタ回路③ 微分回路と積分回路

【フィルタ回路は微積分回路】

そもそも、ハイパスフィルタ、ローパスフィルタは低周波除去や高周波除去目的として使用しますが、減衰帯域（除去帯域）は微分回路・積分回路としてアナログ演算に用いることができます。もう一度ボード線図を見てみましょう。

上がハイパス、下がローパスフィルタの特性です。ハイパスの場合、f0×0.1の周波数で位相が90°進んでいました。ということはVinがsin波の場合Voutはcos波になっているということです。つまり、これは入力信号を微分したことになります。同様にローパスの場合、f0×10の周波数で位相が90°遅れていました。ということはVinがcos波の場合Voutはsin波になっているということです。つまり、これは入力信号を積分したことになります。フィルタ回路では切り捨てられる部分も、演算回路として有効利用できるということですね。

関連記事：
フィルタ回路② ボード線図 2011-03-06
フィルタ回路④ ひっくり返せば逆フィルタ 2011-03-21
微分回路と積分回路 2008-10-16

フィルタ回路② ボード線図

ハイパスフィルタとローパスフィルタの周波数特性（Vout / Vin）を図のグラフに表します。縦軸の振幅比、横軸の周波数共にログスケール（対数）で、このような特性図をボード線図といいます。

ハイパスもローパスも共振周波数：f0(ω0)を境にVoutが低減していくことが分かりますね。よってf0(ω0) をフィルタ回路では「カットオフ周波数：fc 」といいます。ハイパスではf0(ω0)の1/10の周波数でVoutは1/10となり、ローパスではf0(ω0)の10倍の周波数でVoutは1/10となります。f0(ω0)において位相回転が45°であることも重要ポイントです。


＊カットオフ周波数を求める式のおさらい。

ω0＝1/ CR［rad/sec］　　f0＝1/ 2πCR［Hz］
ω0＝R/ L［rad/sec］　　 f0＝R/ 2πL［Hz］

関連記事：
フィルタ回路③ 微分回路と積分回路 2011-03-11 21:26:31
フィルタ回路① LRとCR 2011-03-03

フィルタ回路① LRとCR

図のVLとVcの値はどうなるでしょう。インピーダンス：ZL＝ωL （Ω）、Zc＝1/ωC（Ω）が、周波数に依存して抵抗値が変わることがポイントです。左の、抵抗分圧回路のVRなら話は簡単ですね。電源が直流であれ交流であれVRは次式で求められます。

VR={ R2/ (R1+R2) }×Vac

しかし、VLやVcの場合も、AC電源の周波数変化に対する応答の傾向をつかむだけであれば、抵抗分圧とまったく同様に考えて問題ありません。やってみましょう。

VL={ ωL/ (R+ωL) }×Vac　　　　{ } の中の分母分子をωLで割って、
VL={ 1/ (R/ωL +1) }×Vac　　

この式より周波数：ωが限りなく大きくなるとVL= Vacとなり、限りなく小さくなるとVL=0となることが分かります。次、Vcにいきましょう。

VC={ ( 1/ωC) / (R+1/ωC) }×Vac　　　{ } の中の分母分子にωCを掛けて、
VC={ ( 1/ (ωC R+1 ) }×Vac　

この式より周波数：ω が限りなく大きくなるとVc= 0となり、限りなく小さくなるとVc= Vac となることが分かります。（まあ、このように計算しなくても、ZL=ωL 、Zc=1/ωCからおおよその検討をつけることもできますが。）

そもそもフィルタとは必要なものを通し、不要なものを除去するものです。上のコイル回路は入力(Vac)の周波数が高ければ出力のVLは大きくなり、入力の周波数が低ければ出力のVLは小さくなります。これは高い周波数を通し低い周波数を除去していると考えられるので、これはフィルタといえます。そして、高い周波数を通すものを「ハイパスフィルタ」（Hi Pass）といい、低い周波数を通すものを「ローパスフィルタ」（Lo Pass）といいます。

図の回路の場合、コイル回路がハイパスフィルタ、コンデンサ回路がローパスフィルタということですね。蛇足ですが抵抗回路はフィルタではありません。

では少しくわしくフィルタ回路を見ていきましょう。RLフィルタ回路とRCフィルタ回路を一般化して描くと下図のようになります。だいぶ違うようにも見えますが、IN－GND間にAC電源をいれてみてください。さっきの回路と同じであることがじわじわ見えてくると思います。

さて、ではINにAC電圧を加えてみましょう。周波数は、まずはf0 (ω0)で表される共振周波数とします。共振周波数はCRの場合ω0＝1/CR （rad/sec）でした。LRの場合は時定数＝L/Rですから、ω0＝R/L （rad/sec）となります。よってf0＝R/2πL(Hz)です。この共振周波数ではRとLが同じインピーダンスになるのですから、直感的にVOUT＝VIN/2になるのではないかという気がします。ところがどっこい、交流回路ではそうは問屋が卸してくれません。位相の問題があるからです。

Rの場合は両端の電圧と流れる電流の位相は同位相ですが、Lの場合は電圧に対して電流の位相は90°遅れます。Cの場合は電圧に対して電流の位相は90°進みます。

よってLCを含む交流回路は位相を扱うために、ベクトルで考える必要があるのです。ではRLのハイパスフィルタでやってみましょう。RとLは直列ですから電流ｉ がRにもLにも流れます。ｉ によってRの両端に発生する電圧VRはｉ と同位相ですから、ベクトル図ではｉ に重なります。しかしLの両端に発生する電圧VLはｉ に対し90°位相が進みますので、大きさはVRと同じですがｉ に直交して上向きになります。VR＋VL＝Vinですからベクトル和は赤矢印で示すVinのようになります。（左のベクトル図）

VinとVoutで構成される三角形は二等辺直角三角形ですから、Vinを基準（0°）とすると、VLは45°の位相進みであり、Vinに対する大きさはVL＝Vin×（1/√2）となります。Vout＝VLであり、1/√2 ≒0.707ですから、VoutはVinの約70%となります。直感的にVinの半分ではないかと思ったVoutですが、実際にはかなり大きな値でしたね。CRのローパスフィルタの場合は、ハイパスフィルタの逆になるだけですから、ベクトル図と結果のみを示します。

また、これは複素インピーダンス（ベクトルインピーダンス）：jωL、1/jωC を使えば簡単な代数計算で解くことができます。下の「関連記事」を参照してください。　

関連記事：
フィルタ回路② ボード線図 2011-03-06
ベクトルと複素数 2010-12-18
複素インピーダンス（jωLと1/jωC） 2010-12-22 20:16:33

交流回路のまとめ②

【図の条件にて、ベクトルI（A）を求める】

合成インピーダンスは
Z＝｛（R＋jωL）× 1/ jωC｝/｛（R＋jωL）＋1/ jωC｝
Z＝（R/ jωC＋L/C）/｛R＋j（ωL－1/ωC）｝

各パラメータに数値を入れる。
Z＝（8－j4）/（2＋j2）

分母分子に共役複素数を掛ける。
Z＝｛（8－j4）（2－j2）｝/｛（2＋j2）（2－j2）｝
Z＝（16－j16－j8－8）/（4＋4）
Z＝（8－j24）/ 8
Z＝1－j3　　　　（これが本回路の合成インピーダンスである）

電源電圧、ベクトルVはV＝10（V）∠0だから、求めるべきベクトルI は、
I＝10 /（1－j3）
I＝｛10（1＋j3）｝/｛（1－j3）（1＋j3）｝
I＝（10＋j30）/（1＋9）
I＝1＋j3　　　（絶対値と偏角は　√10 ∠atan 3　＝∠π/2.5［rad］）


【交流の電力】
次に、本回路の消費電力を求める。
VI＝10×（1＋j3）
VI＝10＋j30

よって、有効電力P＝10［W］、無効電力Q＝30［var］である。
皮相電力Sは
VI＝31.6［VA］　［＝√（10^2＋30^2）］

関連記事：
交流回路のまとめ① 2011-01-21
ラジアンの話 2007-08-20

電界と磁界の記号と単位

電荷［Q］（電気量）　C（クーロン）　1C＝1A・s
磁荷［m］（磁気量）　Wb（ウェーバ）　1Wb＝1V・s

電束［　］（電気力線）　C（クーロン）　1C＝1A・s
磁束［φ］（磁力線）　Wb（ウェーバ）　1Wb＝1V・s

電界（の強さ）［E］　V/m
磁界（の強さ）［H］　A/m

電束密度［D］　　　　　　　　　＝1C/m^2　［D＝εE］
磁束密度［B］　T（テスラ）　1T＝1Wb/m^2　［B＝μH］

キャパシタンス［C］　F（ファラド）　1F＝1C/V　（クーロン/V）
インダクタンス［L］　H（ヘンリー）　1H=1Wb/A

誘電率［ε］　F/m（ファラド毎メートル）
透磁率［μ］　H/m（ヘンリー毎メートル）

［電束密度D＝εE　磁束密度B＝μH］

＊以上、V：ボルト　A：アンペア

関連記事：
電荷と電気① 電池 2011-01-27
インダクタンスと磁気 2009-10-01

電荷と電気③ 電気力線と電束

プラスに帯電した導体とマイナスに帯電した導体の間には「電界」が生じます。これを考えやすくするために、電界を「電気力線」で表します。これは磁気において、磁界を表す磁力線と同じです。

平行平板の電気力線は、距離が離れている場合は、平板内の電荷が均一に分布し、電気力線は放射状になり湾曲しますが、距離を非常に短くすれば正電荷と負電荷が引き合い、電荷が平板の向い合う面に集まります。電気力線は電荷1個につき1本と定義しますので、隙間の狭い並行平板間の電気力線の数は増加し、電気力線の形状はすべてがほぼ平行に（直線に）なります。

電気力線を総じて電束といい、単位面積あたりの電気力線の数を電束密度（D）といいます。つまり平板の面積が同じであれば、距離の離れた平板間より距離の短い平板間の方が、電束密度が大きいということです。これも、磁気における、磁束（Wb）や磁束密度（B）と同じです。なお、電荷の数と電気力線の数は1：1に対応しますので、互いに置き換えて扱うことが可能であることから、電束もQ［クーロン］で表します。

さて、静電容量C（F）は、C＝εS/l　です。（S：平板の面積、l：平板間の距離、ε：誘電率）
電界の強さをEとすると、電束密度（D）と誘電率（ε）との関係は次式で表されます。
E＝D/ε　　（D＝εE）

＊D＝εE　は　 B＝μH　に相当します。
（B：磁束密度、μ：透磁率、H：磁界の強さ）


図のように平板間に絶縁体を入れると、電気力線の数（電束）は電荷の数だから変化しませんが、誘電率（ε）が大きくなるため、上式より電界の強さEが小さくなります。これをコンデンサとして考えてみれば、電界の強さEは電位差（電圧）ですから、絶縁体の誘電率によって静電容量が増えたのだということが分かりますね。
V＝Q/C　（Q＝CV）　　［空気：ε＝1、マイカ：ε＝2.5］

平行平板を電池などの電圧源に接続して平板を帯電させ、電界の大きさEを一定に保てば、D＝εE より、絶縁体を入れてεを大きくすることにより、平板間の電束密度Dが大きくなります。この電束密度は平板間の電気力線の本数（電荷の個数）に一致しますから、絶縁体（誘電体）を入れることにより電荷Qが増加することを意味しますね。これもコンデンサの静電容量（F）の大小から納得できることです。

関連記事：電荷と電気② コンデンサ 2011-02-01

電荷と電気② コンデンサ

電荷と電気① 電池
【コンデンサによる電荷のチャージ】

次に豆電球に付いているマイナス電極側の電線にコンデンサを挿入してみましょう。このときコンデンサは電荷を溜めていないものとします。またコンデンサのプラス電極側の平板を「A平板」、マイナス電極側の平板を「B平板」とします。

乾電池に電線を接続した瞬間に、プラス電極側の電線はプラス電極と同電位になり、マイナス電極側の電線とB平板はマイナス電極と同電位になります。そしてコンデンサは電荷を溜めていないのでA平板とB平板間に電位差は無く、よってA平板とこれにつながる電線の電位もマイナス電極と同電位になります。するとフィラメントの両端に1.5Vの電位差が生じることになります。

フィラメントは一種の抵抗線ですから、抵抗値＝Rとすると、1.5/R（A）に相当する電荷（電子）がフィラメントに流れます。すなわち、コンデンサのA平板からフィラメントを経て電池のプラス極に電子が流れ込みA平板には相対的に正電荷が溜まり始めます。またB平板はA平板の正電荷に相当する（極性が釣合う）負電荷を溜めるために、電池のマイナス極から電子が供給され負電荷が溜まり始めます。すると、A平板の正電荷とB平板の負電荷によって、平板間に電位差が生じます。すると、その分フィラメントの電位差が小さくなり、電流が減少します。

このようにして、A平板の正電荷とB平板の負電荷は増加していき、平板間の電位差が1.5Vに達するとフィラメントの端子間電圧がゼロとなり、回路の電荷の流れ（電流）は止まります。コンデンサはこのようにして電荷（電気量）をチャージするわけですね。溜めた電荷の量はQ＝CVです。Cの容量値（F）が大きいほど、また端子間電圧Vが大きいほど、多くの電荷が溜まるということです。

次に、電池を取去って電線を短絡（接続）するとどうなるでしょう（右図参照）。コンデンサが蓄えた正電荷と負電荷によって、A平板とB平板の電位差は1.5Vになっています。ということはフィラメントの端子間に1.5Vの電圧が加わり、コンデンサの正電荷が電線の電子を吸込み、負電荷が電子を供給して、電池を接続したときとは逆の方向に電流が流れ始めます。これによって、コンデンサの正電荷と負電荷は共に減少し、平板間の電位差が小さくなります。そして、蓄えていた正電荷と負電荷が無くなれば、平板間電圧はゼロとなって電流は止まります。これがコンデンサによる放電です。

乾電池は電荷を回路に供給しても、電池内部ですぐに電荷を生成するので、電流を流し続けることができますが、コンデンサの場合は溜めた電荷の量しか電流を流せないということですね。

関連記事：
電荷と電気③ 電気力線と電束 2011-02-06
電荷と電気① 電池 2011-01-27

電荷と電気① 電池

「電気とは何でしょう？」この問いはかなり難しい問題です。一般的には「電圧」と「電流」、この2つのワードを持ち出せば、おおむね電気を捉えていると言えるでしょう。しかし、では電圧とは何？電流とは何？と考えを進めると、簡潔で明確な言葉がなかなかすぐには出てきません。

実は、簡潔で明確な言葉があるのです。それが「電荷」です。まず始めに電荷ありき。電圧も電流も電荷の振る舞いです。電荷はコンデンサの特性を考えるときに、なじみのある言葉として出てきますね。Q＝CV　のように、電荷は記号Qで表され、単位はC［クーロン］です。

電荷から電気を考えるときに、乾電池の構造と原理がそれを分かりやすく説明してくれます。図を見てください。単純化して示していますが、乾電池（マンガン）は図のように、亜鉛缶の容器に電解液を溜め、電解液に炭素棒を差し込んだ構造になっています。そして、これらの化学反応によって、亜鉛からは電子を残してプラスイオンが追い出され、それが炭素棒にいき、炭素棒から不足分の電子をもらって結合し中性（アンモニウム）になります。このようにして、亜鉛は電子が余りマイナスに帯電し、炭素棒は電子が不足してプラスに帯電します。

この亜鉛に余ったもの（相対的に増加したもの）、つまり電子が電荷、正しくは負電荷であり、炭素棒に残った電子の穴が正電荷です。この亜鉛の負電荷と炭素棒の正電荷により、亜鉛缶と炭素棒の間に電位差（電圧）が生じます。乾電池の場合は1.5Vですね。

電荷は「電気量」とも表します。つまり、あたかもバケツに溜めた水のように、電気には量としての大小があるのです。電気の量とはすなわち電荷の数であり、負電荷である電子、正電荷である電子の抜けた穴、これらの数を意味します。これは、容量の大きなコンデンサには多くの電荷が溜まることからも、概念的に理解できますね。

さて、乾電池に豆電球をつなぐと、豆電球は点灯します。これは豆電球のフィラメントに電流が流れるからです。では電流とはいったい何の流れでしょう。これは皆さんすでにご存知のように電子の流れ、つまり負電荷が流れるということです。「電流とは電荷の流れ」これが、より電気の意味に近い概念です。豆電球には2本の電線が付いています。これを、フィラメントを介した1本の電線とみなせば、電線内の電子は乾電池のプラス電極（炭素棒）の吸引力によって引込まれ、マイナス電極（亜鉛）の反発力によって押されて電線内を移動します。炭素棒に吸い込まれて不足した電子は亜鉛から瞬時に供給されて、電線内では一定量の電子の流れ、つまり電荷の流れが継続しこれが電流になるわけですね。

一方、電池の亜鉛缶と炭素棒に着目して見れば、電線に電流を流すことで亜鉛の負電荷と炭素棒の正電荷が共に減少しますが、乾電池内の化学反応によって瞬時に補われ、亜鉛缶の負電荷と炭素棒の正電荷は常に一定量に保たれます。よって、電流（電子：負電荷）が流れているときも、電圧は1.5Vに保たれるということです。

負電荷は電子が担いますが、単位：1C［クーロン］は、電子1個の電荷のことではありません。Q＝CVより、端子電圧＝1Vの1Fのコンデンサが溜めている電荷が1Cです。あるいは、「1C の電荷が1J の仕事をする電位差を1V と定義する」（Wikipedia)ということです。また、電線（導体）を1秒間に1Cの電荷が通過するとき、これを1Aの電流と定義します。

関連記事：
電荷と電気② コンデンサ 2011-02-01
電界と磁界の記号と単位 2011-02-14

交流回路のまとめ①

【左の回路のベクトルVを求める】

合成インピーダンスは
Z＝1/ jωC＋ 2jωL /（2＋jωL）

各パラメータに数値を入れる。
Z＝1/ j0.5＋ j8/（2＋j4）

式を整える。
Z＝－j2＋ j4/（1＋j2）

第2項に共役複素数を掛ける。
Z＝－j2＋｛j4（1－j2）｝/（1＋4）
Z＝－j2＋（j4＋8）/5
Z＝－j2＋j4/5＋8/5
Z＝8/5＋j4/5－j10/5
Z＝8/5－j6/5　　　　（これが本回路の合成インピーダンスである）

回路電流ベクトルIはI＝5（A）∠0だから、求めるべきベクトルVは、
V＝5（8/5－j6/5）
V＝8－j6　　（絶対値と偏角は　10∠atan－6/8　＝∠－π/4.88［rad］）　


［交流の電力］
次に、本回路の消費電力を求める。
VI＝5×（8－j6）
VI＝40－j30

よって、有効電力P＝40［W］、無効電力Q＝30［var］である。
皮相電力Sは
VI＝50［VA］　｛＝√（402＋302）｝


【右の回路のベクトルIを求める】

負荷の複素インピーダンス（ベクトルインピーダンス）は
Z＝8/5－j6/5

だから、回路電流ベクトルIは
I＝8/（8/5－j6/5）
I＝40/（8－j6）

分母分子に共役複素数：8＋j6　をかけて
I＝40（8＋j6）/（64＋36）
I＝320/100＋j（240/100）

よって
I＝3.2＋j2.4　　（絶対値と偏角は　4∠atan 2.4/3.2　＝∠π/4.88［rad]）

関連記事：
複素インピーダンス（jωLと1/jωC） 2010-12-22
ベクトルと複素数 2010-12-18
交流回路のまとめ② 2011-02-21

テブナンの定理 と 重ね合わせの理 ②

（キルヒホッフにて　i1＝0.53　 i2＝0.55　 i3＝1.08　）

【重ね合わせの理】
テブナンの定理を使うことで電気回路の計算がずいぶん楽になりましたが、もうひとつ「重ね合わせの理」という妙手があります。やってみましょう。

左上の図が元回路です。これを中の図、下の図のように片方の電源を短絡して各電流を求めてみます。

8Vの電源から流れる電流は
i1a＝8/（9＋15/8）　＝0.74
i2a＝0.74×3/8　＝0.28 → －0.28（i2に対して逆）
i3a＝0.74－0.28　＝0.46

6Vの電源から流れる電流は
i2b＝6/（5＋27/12）　＝0.83
i1b＝0.83×3/12　＝0.21 → －0.21（i1に対して逆）
i3b＝0.83－0.21　＝0.62


そして、電流aと電流bを足します。この重ねあわせに“理”があります。
i1＝i1a＋i1b　＝0.74－0.21　＝0.53
i2＝i2a＋i2b　＝－0.28＋0.83　＝0.55
i3＝i3a＋i3b　＝0.46＋0.62　＝1.08

となって、キルヒホッフで求めた各電流と一致しましたね。
何か狐につままれたような感じですが、これが「重ね合わせの理」です。
すごいっすね。（＾＾）


［テブナンの定理の補足］
右列の図を見てください。テブナンの定理を使って、9Ωに流れる電流i1を求めてみましょう。

ルールに沿って9Ωを取払い、まずa-b間電圧を求めます。これは8Vが直列に入るので少しややこしいですが、a-G間電を求めて8Vを引けばa-b間電圧になりますね。OKですか？（＾＾）

V（a-b）＝6×（3/8）－8
V（a-b）＝2.25－8　＝－5.75　

端子a-bから見た回路インピーダンスは5Ωと3Ωの並列ですから、
Ri＝15/8　＝1.88Ω

よって、元の回路は等価回路1に置き換えられます。
　
故に、 i1＝－5.75/（1.88＋9）　よって
i1＝－0.53　

マイナスが付いているのは、電流がb→aに流れているということです。よって
i1＝0.53　となります。はい目出度し。

しかし、この場合は電圧計算が少しややこしくなるので、もう少し大胆にいきましょう。
9Ωのみを取払うのではなく、8Vの電源ごと取払ってしまえば、実にシンプルに考えることができます。この場合は等価回路2になります。結果はもちろん同じです。

こっちのほうがエレガントですね。テブナンの定理は柔軟に扱うのが肝要かと。

関連記事：テブナンの定理 と 重ね合わせの理 ① 2011-01-08