脳の解釈が間違えるとき

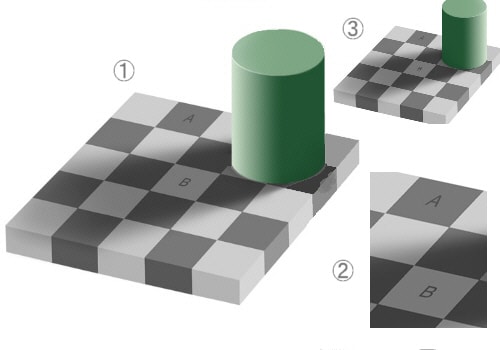
　図①のＡとＢの桝目はＡのほうが明らかに黒く見えますが、実はこれは同じ濃さのグレーです。
　この部分を拡大したのが②図なのですが、拡大してみてもＡの桝目のほうがどうしても濃い色に見えるでしょう。
　どうしてＡのほうが濃く見えてしまうのかということを、心理学の説では脳がＡは黒い桝目に光が当たっていて、Ｂは白い桝目が陰になっていると解釈するからだとしています。
　つまりＢは本当は白であるのになのに、円筒の影のために灰色になっていると脳が解釈するので、黒であるＡに比べれば白っぽく見えるというのです。
　
　このように説明されればなるほどと思うかもしれません。
　人間の脳は複雑な解釈を瞬間的にしてしまうので、実際は同じ色なのにＡとＢは違う濃さの色だと感じるのだと納得してしまうのです。
　つまりこの場合は、網膜上ではＡとＢは同じ色として映っているのに、脳が間隔を否定して違う色だと判断するというのです。
　間隔に忠実であれば間違えないですむのに、脳が理論的解釈をするために錯覚に陥ってしまうということでしょうか。

　ところで図①は実はイタズラがほどこされているもので、元の図形はエーデルソンというアメリカの心理学者が考案した図③です。
　元の図形では円筒に右から光が当たっているようになっているのですが、①図では円筒には左から光が当たっているように変えてあります。
　したがってＢの部分は円筒の影になっているということはなく、Ａと同じように光が当たっていると解釈すべきです。
　Ｂの部分は陰になっていると脳が解釈するので錯覚が生ずるというのは、あとから考えた説明で、そんなことを考えなくてもＡのほうが濃く見えるのです。
　実際②図のように部分的に取り出した場合でも、Ａのほうが濃く見えるのですから、円筒形というのは影を思いつかせるための小道具だったのです。

　ではなぜＡのほうがＢより濃く見えるかというと、②図で見れば分るように、Ａの桝目は周囲を明るい桝目で囲まれ、Ｂの桝目は濃い色の桝目で囲まれています。
　そのためＡは実際より濃く感じられ、Ｂは実際より明るく感じられるという対比効果によるのです。
　もし②図でＡに視線を集中させて見続ければ、Ａはやや薄く見えるようになり、逆にＢはやや濃く見えるようになって、ＡとＢは実は同じ濃さの色だということが分ります（Ｂに視線を集中しても同じ)。

　②図を見るとき視線を動かせばＡは周囲の白っぽい桝目と比較されますし、Ｂも周囲の黒い桝目と比較されると同時に、Ｂは白っぽい桝目の系列に、Ａは黒っぽい桝目の系列に見えます。
　ところが視線を動かさずＡとＢを同時に見ればＡとＢの色の濃さは同じように見えます。
　つまり視覚的判断といっても、視線を動かすかどうかとか、集中させるかどうかなどによって変わるので、脳の解釈ばかりに注意を向けるべきではないのです。

理屈に注意を向けすぎる錯思

　図の平行四辺形の中の対角線ＡとＢは同じ長さなのですが、Ａのほうが長く見えます。
　大人と比べると子供のほうがＡがＢより余計に長く感じる傾向があり、心理学では子供のほうが特定のものに視線を集中させるからだとしています。
　視線をを集中させるとその場所が膨張して見えるのですが、子供は大きな面積を持つ平行四辺形のほうに注意を集中させるので、Ａのほうが長く見えてしまうと心理学では説明しています。
　つまり子供は最初に目を引くものに引きずられて、その外見だけから判断してしまう傾向が強いというわけです。
　一面的な判断をして、ほかの見方をしたり、全体に注意を向けたりしないために錯覚するというのです。

　ところで錯覚が生ずるのは視線が大きい方の平行四辺形のほうに集中するからというのですが、これは正しいのでしょうか。
　一般的には視線は図形の線が拡散しているところより、集中しているほうに向かうので、逆ではないかと思われます。
　実際にこの図を自然に見るとき、小さいほうの平行四辺形のほうに視線が集中しているのではないでしょうか。
　そうして線Ｂのほうに注意を集中してもＢのほうが長くは見えません。
　二つの線のうち片方を注意を集中して見ているとき、もう片方はよく目に入らないので、長さの比較はできていないのです。

　Ａのほうが長く見える理由付けとしては別の説明もあります。
　ひとつは、下の図のように矢羽の図形を比べると、矢羽の角度が大きいほうが軸線が長く見え、角度が小さいと軸線が短く見えるためだというものです。
　矢羽の角度が小さいほうが軸線の長さが短く見える理由は示されていませんが、実際にそのように見えるのは確かなので、同じ原理が働いていると考えることはできます。

　もうひとつの説明は線ＡとＢに向かい合っている対角ａとｂは同じ大きさなのですが、ｂのほうが大きく見えます。
　そのため角ｂに対している線Ａのほうが長く見えるのです。
　角ｂのほうが大きく見えるのは隣接している角がａの場合より小さいので相対的に大きく見えるのではないかと思われます。
　
　このように線Ａが線Ｂより長く見える理由は、Ａのほうに視線を集中してしまうためとは限らないのです。
　視線を集中させると物が大きく見えるということは事実でも、ものが大きく見えた原因は視線を集中したためとは限らないのです。
　子供の判断が一面的で、目立つものに引きずられてしまうという知識があるため、それに合うような理由付けを考えてしまったのかもしれません。
　子供が視覚的判断から出られず錯覚をするのと反対に、学者や大人は言葉や理論で目だったものに気を奪われて、それに引きずられてしまう恐れがあるのです。
　

数の判断と言葉

　図Ａを幼児に見せて、白い丸と黒い丸とでどちらが数が多いかを聞けば、白い丸のほうが多いと正解します。
　ところがＢ図についてはどうかと聞くと、黒い丸のほうが多いと答えてしまう子供がいるそうです。
　Ａ図の場合は白丸と黒丸が同じ間隔で並んでいるために、空間的に広がっているほうが数が多かったのですが、Ｂ図の場合は間隔が違うために、空間的配置の広がりと数とが一致していません。
　Ｂ図で黒丸のほうが多いと答えてしまう子供は、空間的な広がりという視覚的な判断から、数をも判断してしまっています。

　これは子供が数を数えないで視覚的な印象から判断してしまうためですが、大人でも０.５秒ぐらいの短時間の表示で判断を求められれば、数を時間内に数え切れないので視覚的判断に頼らざるをえなくなり、間違える可能性が出てきます。
　
　Ｄ図とＥ図で、白丸の数がＣ図の黒丸の数と同じなのはどちらかと聞かれたとき、数を数えないで視覚だけで判断するとＤのほうだと答えてしまいがちです。
　この場合は全体的な配置の形が似ているほうが数も同じように感じるからで、視覚的な類似性に頼って判断するためです。
　
　言葉を使わないで数えるということは、大人になっても難しいことで、言葉を持たないサルが計算までするとなれば驚くべきことかもしれません。
　言葉を使わないで数を数えるのがどれだけ難しいかは、図Cで目で順に黒丸を追いながら、「イチ、イチ、イチ、、、」と口で言い、最後まで来たとき何個目かを答えようとすれば分ります。
　「イチ、ニ、サン、、」と順に数を口にすれば、自動的にいくつかを答えられるのですが、順序に関係しない言葉を言いながらでは、答えが出せなくなるのです。
　
　音読だけでなく簡単な計算をすると前頭葉の血流が増加するというのも、簡単な計算というのが言葉を使っていて、言葉を使うという点では共通な部分があるからかもしれません。
　複雑な計算や、難しい数学の問題を考えるときはかえって言葉はとまってしまっていますから、簡単な計算を繰り返す場合より脳血流が増加しないのでしょう。
　簡単な計算を繰り返すほうが脳血流が増加するからといって、簡単な計算ばかりしていては数学的能力は進歩しないでしょう。
　ソロバンの熟達者ように言葉を使わないで、自動的に指を動かして作業するという場合、ほとんど前頭葉の血流が増加しないのもうなずけるのです。
　ソロバンの例だけでなく、技術や技能が高度化した場合は、言葉を使わなくなるので、脳血流が余分に増えるということはありません。
　脳血流が増えるというのは未熟な段階を示しているのですから、ゲームをやっている若者の脳血流が少なかったからといって、痴呆と決め付けるのは早計なのです。

アナログ的な計算能力

　　上の図は数字が瞬間的に表示されてから消えたあと、数字の小さな順に位置を手でタッチして答えさせるテストです。
　下の図は、いくつかの点が瞬間的に表示されてから消え、そのあともう一組の点が表示されて消え、次の画面で前の二つの点の数の合計を答えさせるテストです。
　上の図の場合はチンパンジーを使ったテストで、この場合は子供のチンパンジーの成績は、日本の大学生の成績を上回っています。
　これに対し、下の図はマカクサルを使ったテストで、この場合は対象とされたアメリカの学生の成績はサルの成績を上回っています。

　これはなにもアメリカの学生のほうが、日本の学生よりも優れているということを示しているわけではありません。
　上の図のテストではチンパンジーが数字を理解しているといっても、順序として覚えているだけす。
　子、丑、寅、卯、竜、、とか、月、火、水、木、、という文字のように順序を示す文字として覚えているので、数をあらわす数字として覚えているわけではありません。
　チンパンジーは数字を順番として理解していて、瞬間的に表示された数字の位置と種類を記憶して、数字の順番に従って位置を答えたのです。
　したがってここでは、数字の理解力が示されたというよりも、短期記憶の能力が示されたということになります。
　これに対して下の図の場合は数字が示されるのではなく、数が点の数として表示されています。
　したがってここでは記号を記憶する能力ではなく、数を判断して記憶して計算するする能力が示されるということになります。

　上の図の場合は文字の間の順序を理解していれば、成績を左右するのは視覚的な短期記憶力です。
　下の図の場合は視覚的な記憶力だけでなく、足し算をするという計算能力が成績を左右します。
　サルの種類の違いはありますが、サルは視覚能力の点では人間を上回る能力を持ちうるが、計算能力では劣るということが示されています。
　
　計算といっても２＋２＝４といったごく簡単な計算でさえ１００％の正答率にならないので、人間が普段やっている計算とは違います。
　正解率は選択肢が４と８の場合より４と３のように離れているほうが成績がよくなるというのですから、答えは「いくつ」というハッキリしたものでなく、「およそこのくらい」という感覚的な、アナログ的なものだということが分ります。
　計算能力といっても記号を使っての計算ではなく、感覚的な把握能力なので人間が考える計算能力ではないのです。
　この場合、人間のほうが成績がよいのは、表示点の数が少ない場合、自動的に数字に変換できてしまう率が高いためです。

　もし感覚的な把握能力を向上させようとするなら、「いくつ」と数字に変換しないで判断するようにすべきでなのです。
　

言葉を使わないで計算する

 米デューク大学Ｅ・ブラノン准教授（認識神経学）の研究では、サルにも足し算の暗算をこなす能力があり、正答率は８割近くに達したということです。
　２匹のマカクザルを使って、スクりーンの前に座らせて画面に複数の点(９個以内)を表示し、その画面を消した後で、異なる個数の点を書いた画面を見せます(上の図のような具合）。
　その後、３枚目の画面として、先の２枚の点の総和となる個数の書かれた画面と間違った総和の画像を同時に見せ、答えを選択させます。
　数日間の空連を行った後では、いずれのサルも正答率は７６％で、同じテストを大学生にさせたところ正答率は94％だったそうです。 
 
　「サルたちは、単に数を数えたり、数字の順序を覚えたりできるだけではなく、頭の中で足し算をすることもでき、しかも、単に足し算ができるだけではなく、大学生とほとんど変わらないほど優秀だ。」などと新聞には紹介されましたがそうなのでしょうか。
　数字の足し算といっても一桁の数同士なので、組み合わせは８１通りで、九九のように結果を暗記させたのではないかと言う人もいますが、訓練は一部の数字だけで行い(たとえば偶数だけ）、テストのときは訓練で使わなかった組み合わせを使っているようなので、暗記の結果ではないようです。

　それより、一桁の数字の足し算で、大学生の正答率が１００％でなく、９４％というのは一体どういうことかと疑問を持つべきでしょう。
　いくらアメリカの大学生のレベルが低いからといって、一桁の足し算の成績が９４点というのは不思議でしょう。
　実はこの計算は、一、二、三と言葉を使って数えることを大学生には禁じています。
　サルは言葉を持たないので、サルと同じように言葉を使わないで数を読取り、計算させようと条件を近づけているのです。
　アラビア数字の一桁の足し算をさせたというわけではないのです。

　スクリーンに表示される点の数が四つ以内なら、表示時間が二十分の一秒程度でも人間は数を瞬間的にとらえられますが、それ以上になると点一個につき四分の一秒程度時間がかかります。
　上の図で数字を示す点が表示されるのは０.５秒となっていますが、表示される点の数が７個以上になれば、言葉で数え終えないうちに消えてしまいます。
　大学生の場合は、規則を破って言葉で数えようとすると、数え切れないで正答できないこともあるという仕掛けになっているのです。

　この実験は言葉を使わないで数を把握し、計算をするというような能力がサルや人間が共有していることを確かめようとしたもので、言葉を使わない場合はサルと人間と能力の差があまりないということを示しているのです。
　たとえば下の図のように、二つの棒の長さを足した長さを答えるというようなアナログ的な問題なら、言葉を使わないのでサルも人間も同じ条件で考えるので、成績もさほど変わらないでしょう。

視覚的判断と抽象能力

　ピタゴラスの定理というのは直角三角形の斜辺の二乗は他の二辺の二乗を加えたものに等しいというもので、①図でいえばaの二乗とｂの二乗を足したものがｃの二乗に等しいというものです。
　ピタゴラスの定理の証明法というのは１００以上もあるということですが、最も視覚的にわかりやすい説明のために②のように斜辺に向かって垂直線を引きます。
　その結果もとの直角三角形は、形が同じで大きさが異なる(相似形の）二つの直角三角形に分割されます。
　このときaの二乗プラスｂの二乗イコールｃの二乗だということが分ります。
　
　なぜか気がつかないとすれば、それは②図を見たとき二つの小さな三角形が見えていて、二つをあわせた大きな三角形を見失っているからです。
　③図は二つの小さな三角形とそれを合わせた大きな三角形をバラしてみせたものです。
　こうしてみると三つの三角形は大きさが違いますが形は同じで、それぞれの面積は辺の長さの二乗に比例します。
　三角形Ａと三角形Ｂを足したものが三角形Ｃですが、それぞれの面積はaの二乗、ｂの二乗、ｃの二乗に比例するのでaの二乗プラスｂの二乗はｃの二乗だということになります。

　②図を見て三角形がいくつあるかと聞かれた場合、うっかり二つと答えてしまう人もいるかもしれませんが、三つだといわれても分からない人というのはまず、いないでしょう。
　チンパンジーの場合は三角形が三つあるということが分らないそうですが、これは目に見える二つの三角形のほかに、同時にこれを合わせた大きな三角形を見ることができないためです。
　大きな三角形の中には線が一本はいっていますが、これを無視しないと大きな三角形は三角形とならないので、大きな三角形を認識するには抽象能力が必要です。

　単純にものをあるがままに見るという視覚能力では、チンパンジーは人間と変わることはなく、むしろ人間よりも優れていたりします。
　人間の場合はただものを見るだけでなく、抽象化によって異なった次元のものを見ることで、そこにある関係を把握することができるのです。
　直角三角形が二つの相似形の三角形に分割できるということから、ピタゴラスの定理を直感的に理解できたりもするのです。