2021年出題。 A〜Fは、1〜9の互いに異なる6個の整数である。 次の3つの関係式が成り立つとき、AとDの差はいくらか。 A✕B✕C=252 B✕D✕E=108 C✕E✕F=70(選択肢省略) 1〜9を使う積の計算パズルです。 この場合は、「5」と「7」を探しにいくのが定跡です。 1〜9の中には、2の倍数が4つ含まれていますし、3の倍数が3つ、4の倍数が2つ含まれています。 でも、5の倍数は「5」のみ、7の倍数は「7」のみです。 だから、いくつかの数を掛け合わせたときに5で割り切れる数になれば、掛け合わせた数の中に、必ず5が含まれていることが分かるのです。 掛け合わせたときに、それが7で割り切れる数になったときも同様です。 ただし、1〜10の場合は、たとえ掛け合わせた数が5で割り切れたとしても、掛け合わせた数の中に必ず「5」が含まれているとは限りませんね。 この場合は、掛け合わせた数の中に「5」か「10」が含まれていたとして考えていきます。 とりあえず、素因数分解します。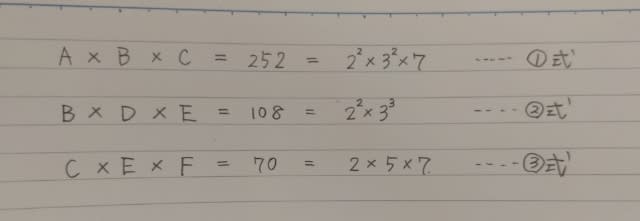
①式より、A、B、Cの中に「7」がいることが分かります。 また、③式より、C、E、Fの中にも「7」がいることが分かります。 もちろん、A、B、C、E、Fの中に7は1つしかないのだから、Cが「7」です。 次に、「5」を見つけましょう。 ①式にも②式にも「5」はいません。 ③式に「5」がいます。 Cは「7」だったので、EかFが「5」です。 でも、Eが「5」だったとすると、②式の掛け算の結果が5で割り切れる数になっていないとおかしい。 よって、Fが「5」。 まるで、「7」がお父さん、「5」がお母さんで、どこに自分の父や母がいるのかを探しているようですね。 ここまでくれば、あとは適当にやれば正解にたどりつけます。
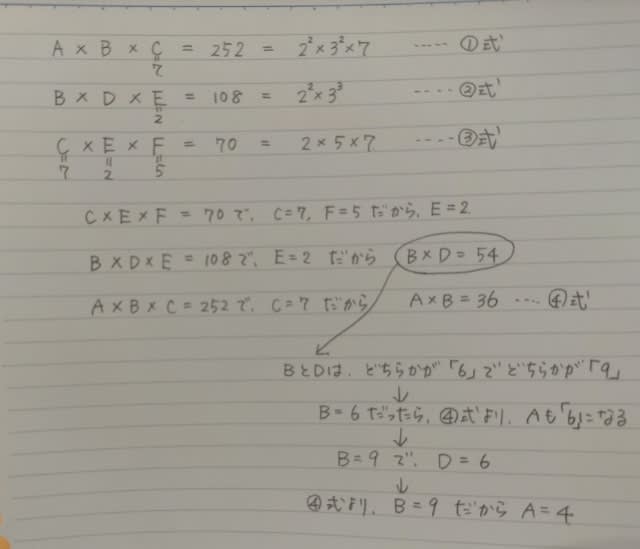
結論は、
AとDの差は6−4=2。 正解は、2です。





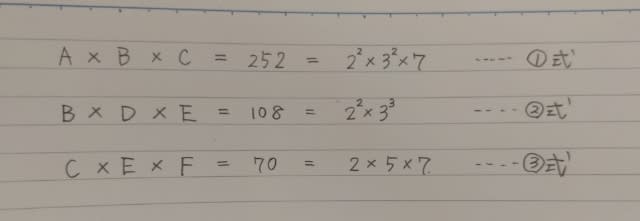
①式より、A、B、Cの中に「7」がいることが分かります。 また、③式より、C、E、Fの中にも「7」がいることが分かります。 もちろん、A、B、C、E、Fの中に7は1つしかないのだから、Cが「7」です。 次に、「5」を見つけましょう。 ①式にも②式にも「5」はいません。 ③式に「5」がいます。 Cは「7」だったので、EかFが「5」です。 でも、Eが「5」だったとすると、②式の掛け算の結果が5で割り切れる数になっていないとおかしい。 よって、Fが「5」。 まるで、「7」がお父さん、「5」がお母さんで、どこに自分の父や母がいるのかを探しているようですね。 ここまでくれば、あとは適当にやれば正解にたどりつけます。

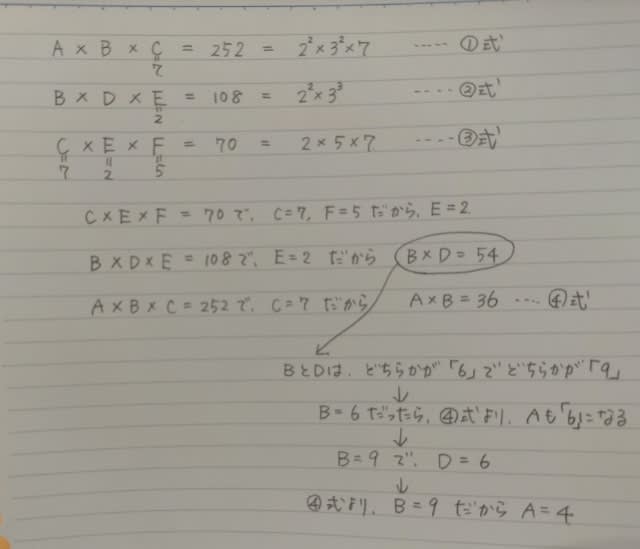
結論は、

AとDの差は6−4=2。 正解は、2です。














