1から6までの互いに異なる数字が1つずつ書かれた6個の球が入っている箱がある。この箱の中から1個の球を取り出し、書かれている数字を確定して元に戻すという操作を3回行うとき、取り出された球に書かれた数字の最大値が4である確率はいくらか。(選択肢は省略) 最大値が4なので、3回とも5または6が出ないのですが、それだけではダメ。 もしも、3回とも1~3の目が出てしまったら、最大値は1または2または3になってしまいます。 よって、求める確率=(3回とも5または6が出ない確率)ー(3回とも1か2か3が出る確率)です。 3回とも5または6が出ないというのは、言い換えると、3回とも1か2か3か4が出るということです。





0、1、2、3、4の5つの数字のうち、相異なる数字を用いてできる3桁の偶数の個数として、最も妥当なのはどれか。 1. 30個 2. 42個 3. 48個 4. 56個 5. 60個 普通というのは、それぞれの位の数が何通りあるかを調べて、掛け合わせるだけということです。並べるカードの中に0が入っていて、偶数が何個できるかという問題は、場合分けが必要なので、これら4パターンの中では、一番よく出題されます。
普通というのは、それぞれの位の数が何通りあるかを調べて、掛け合わせるだけということです。並べるカードの中に0が入っていて、偶数が何個できるかという問題は、場合分けが必要なので、これら4パターンの中では、一番よく出題されます。 このように、1の位が0のときと、1の位が0以外の偶数のときとで、百の位の場合の数が違ってくるからです。
このように、1の位が0のときと、1の位が0以外の偶数のときとで、百の位の場合の数が違ってくるからです。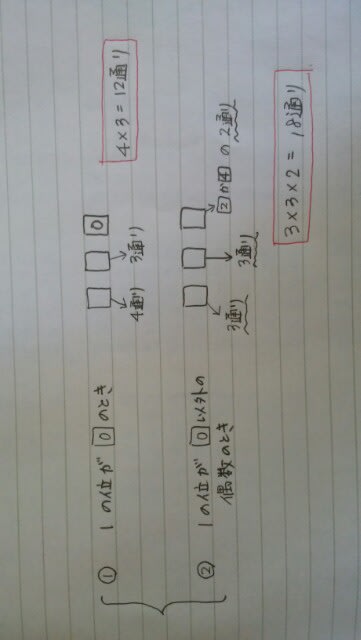 よって、正解は肢1です。
よって、正解は肢1です。
にほんブログ村今日のオマケ 蝉の群団
蝉の群団
 普通というのは、それぞれの位の数が何通りあるかを調べて、掛け合わせるだけということです。並べるカードの中に0が入っていて、偶数が何個できるかという問題は、場合分けが必要なので、これら4パターンの中では、一番よく出題されます。
普通というのは、それぞれの位の数が何通りあるかを調べて、掛け合わせるだけということです。並べるカードの中に0が入っていて、偶数が何個できるかという問題は、場合分けが必要なので、これら4パターンの中では、一番よく出題されます。 このように、1の位が0のときと、1の位が0以外の偶数のときとで、百の位の場合の数が違ってくるからです。
このように、1の位が0のときと、1の位が0以外の偶数のときとで、百の位の場合の数が違ってくるからです。 よって、正解は肢1です。
よって、正解は肢1です。にほんブログ村今日のオマケ
 蝉の群団
蝉の群団
5人の生徒を、A、B、Cの3つの部屋に分ける組み合わせの数として、最も妥当なのはどれか。ただし、どの部屋にも少なくとも1人は入るものとする。①90 ②120 ③150 ④153 ⑤240 2つの考え方があります。その1 5人を、A、B、Cの3つの部屋に分けるならば、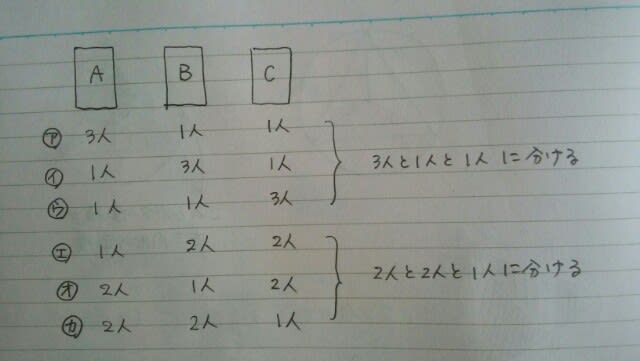

 よって、60+90=150通りで、肢3が正解。アを考える時に、Aの部屋から順番に決めていっても構いません。式は違ってくるものの、必ず同じ答えになります。例えば、
よって、60+90=150通りで、肢3が正解。アを考える時に、Aの部屋から順番に決めていっても構いません。式は違ってくるものの、必ず同じ答えになります。例えば、 その2
その2
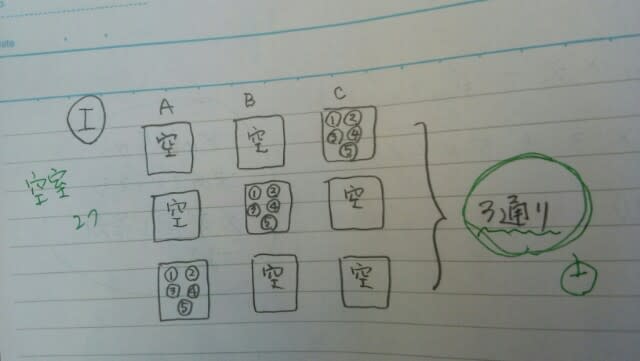

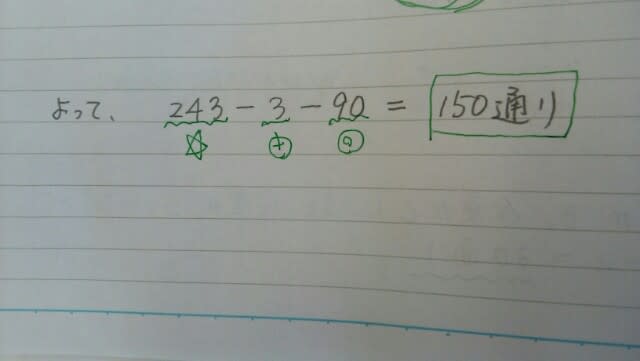


 よって、60+90=150通りで、肢3が正解。アを考える時に、Aの部屋から順番に決めていっても構いません。式は違ってくるものの、必ず同じ答えになります。例えば、
よって、60+90=150通りで、肢3が正解。アを考える時に、Aの部屋から順番に決めていっても構いません。式は違ってくるものの、必ず同じ答えになります。例えば、 その2
その2


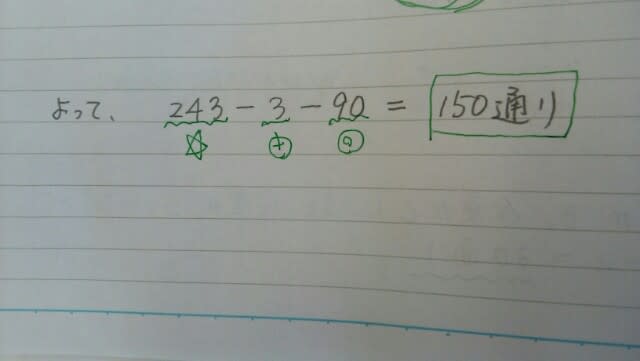
1~5の番号が書かれた5つのボールを青色、赤色、黄色の3つの箱に入れる場合の数と、区別のつかない5つのボールを区別のつかない3つの箱に入れる場合の数の差として、最も妥当なのはどれか。ただし、5つのボールはすべて、いずれかの箱に入れるものとする。 1. 180 2. 197 3.204 4. 221 5.238 すべての箱に最低1個はボールを入れるものとする、という問題はよくあるが、5つのボールはすべて、いずれかの箱に入れるものとする、という条件は、あまり見たことがありません。たとえば、①のボールはどの箱にも入れないなど、あまり考えたりしません。つまり、この条件は、「全てのボールは必ずどれかの箱に入れる」という、当たり前のことをいっているだけです。よって、この問題を考えるときには、空になる箱があってもあっても構わない。 前者は、重複順列なので、3の5乗で、243通り。(①は、青か赤か黄色かで3通り。②も、同様に3通り。③も④も⑤も3通り。その結果、空の箱ができても、こっちの知ったことではない。)後者は、何個入りの箱が何種類できるかだけを聞いています。一番多い箱をa,2番目に多い箱をb,一番少ない箱をc(同じ個数もあり)とすると、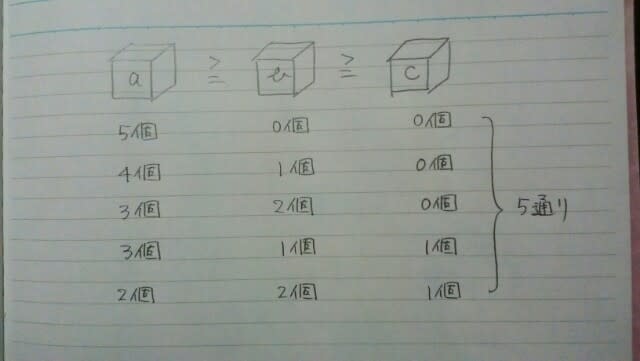 よって、その差は、243-5=238通り。5が正解。
よって、その差は、243-5=238通り。5が正解。
 よって、その差は、243-5=238通り。5が正解。
よって、その差は、243-5=238通り。5が正解。












 よって、4+3+2=9(色)となり、正解は、③でした。
よって、4+3+2=9(色)となり、正解は、③でした。