5肢択一の問題が3問あり、問題を読んでみたところ、サッパリ分からない。そこで、何も考えずに適当に答えた。このとき、2問正解する確率を求めてみます。 例えば、第1問と第2問が正解で、第3問が不正解であれば2問正解となりますので、
そんなこと言うんだったら、第1問と第3問が正解で、第2問が不正解でも2問正解じゃないか。
バカヤロー、第2問と第3問が正解で第1問が不正解でもいいじゃないか。
それ以外は2問正解にはならないなあ、などという議論になり、結局、
となります。 1／5は、正解する確率で、2問正解するから、2乗がくっついていて、4／5は、不正解の確率で、1問が不正解だから、1乗という訳なのですが、「3」は、なぜ「3」なのでしょうか？3問中2問正解が3パターンあるからです。では、なぜ3パターンなのかというと、3つの問題の中から、正解する2問を選ぶのが3通りあるからです。これは、
という意味ですね。まとめてみると、
以上のことから、反復試行の確率の公式ができるのです。 ♡何回やっても、確率が変わらないことを反復して行うときに、♤n回その試行をして、r回Aという事象が現れる確率は、
練習問題を次回やります。ここをポチッとお願いします。→
にほんブログ村
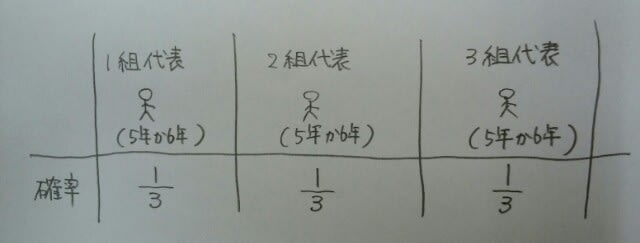もしも、「両方の学年が含まれ」という条件がなければ、単純に、
となりますが、本問は、ここから、3人の代表が3人とも5年生である確率と、3人とも6年生である確率を引かなければなりません。
よって、求める確率は、
正解は、肢⑤です。ここをポチッとお願いします。→
あめ玉は15個なので、あと9個残っています。ここから、2つの考え方があります。その1…重複組み合わせの公式を使う。
その2…○と¦で考える。
ただし、「最低2個」という条件は、始めに満たしてあるので、
というのも可能です。要するに、○9個と、¦2個を、左から順番に並べてやればよいのです。
というわけで、
なお、最後のところは、「同じものを含む順列」と考えて、
としても、全然構わないのです。正解は、肢③です。重複組み合わせは、頻出で、特に果物の買い方の問題はよく出題されます。初めてやる人にとっては、少し難しかったかも？ 
<script type="text/javascript">
例えば、こんな風に座りました。
しかし、まだ2人の先生は、着席していません。2人の先生をg、hとすると、その座り方は、2×1通りあります。
よって、この8人の座り方は、 6！×2×1＝6×5×4×3×2×1×2×1＝1440（通り）で、正解は肢⑤です。
まず、1回目と2回目について整理します。
奇数は、△で囲ってあります。1回目、2回目共に奇数の場合は、掛け合わせるので、
それ以外は足し合わせるので、
これに3回目に出た目を足し合わせて、16以上になるには、2回目までで、10以上なければいけませんね。10以上のものを赤丸で囲みます。
全部まとめて、12＋2＋4＋6＋3＝27通り。サイコロを3回投げるので、目の出かたは、6×6×6＝216通り。よって、求める確率は、
正解は肢3です。