これは選択肢⑤です。 次に、「3個ともバラバラ」という意味だとすると、
これは選択肢にはありません。 正解は、肢⑤です。ここをポチッとお願いします。→
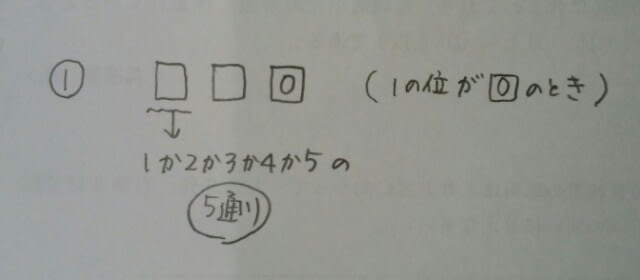仮に100の位が1だったとすると、
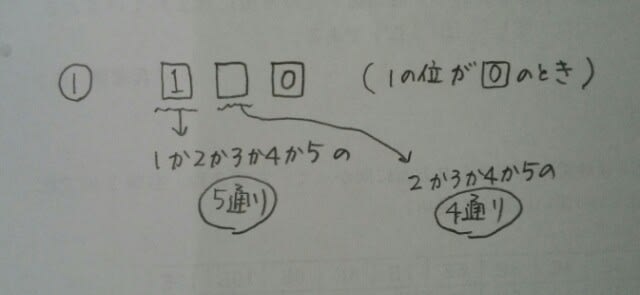よって、5×4＝20通り。
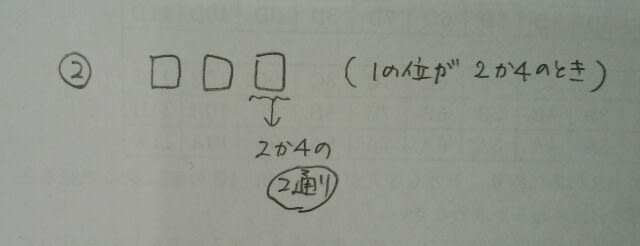仮に1の位が2だとすると、
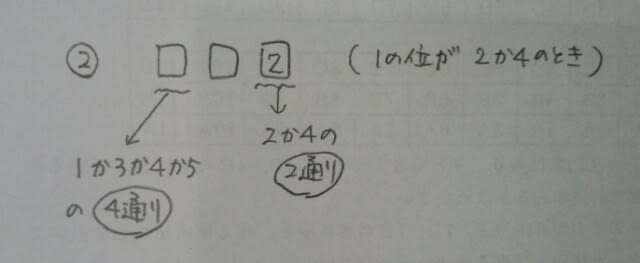仮に100の位が1だとすると、
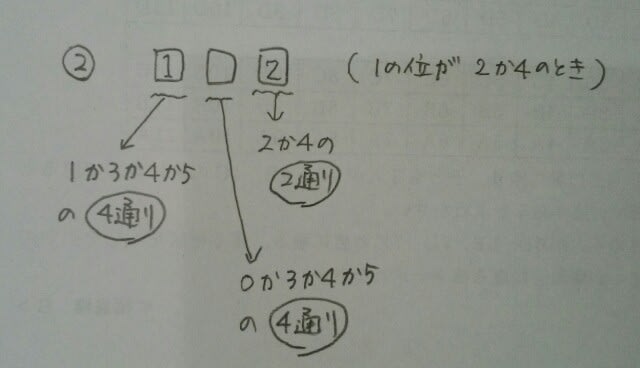という訳で、2×4×4＝32通りです。 まとめると、1の位が0の偶数が20通りあり、1の位が2か4の偶数が32通りあるので、全部で20＋32＝52通りあるので、正解は、肢③です。 えっ！場合分けしたくない？そんなワガママ言う人は、こうして下さい。 まず、奇数とか偶数とか関係なしで、とにかく3桁の整数は何通りできるでしょうか？100の位が5通り（0を入れてはいけない）、10の位が5通り（0を入れても構わない）、1の位が4通りで、5×5×4＝100通りですね。 次に、奇数は何通りあるでしょうか？奇数なら、1の位に0は入らないので、あなたの嫌いな場合分けは不要ですよ。
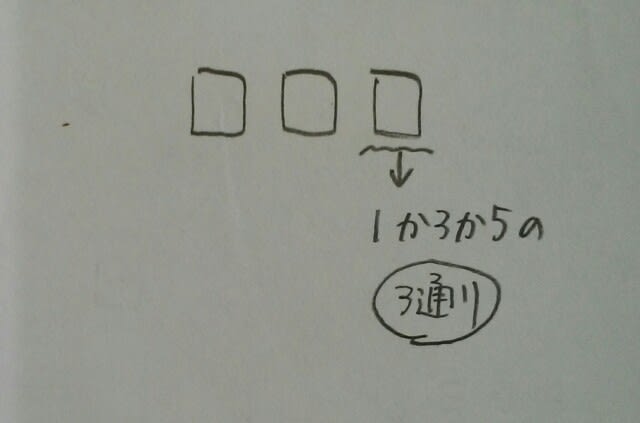仮に1の位が1だとすると、
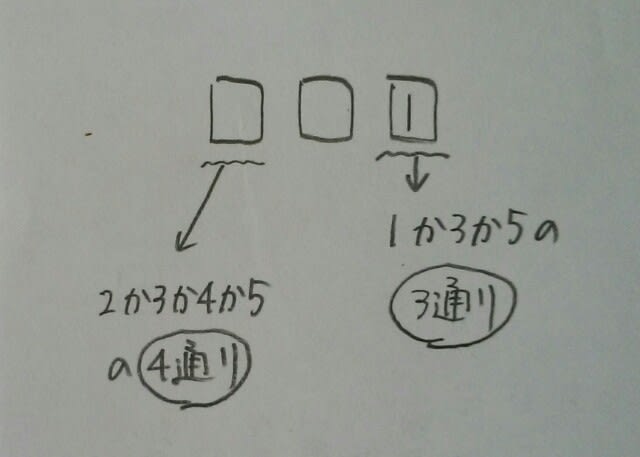仮に100の位が2だとすると、
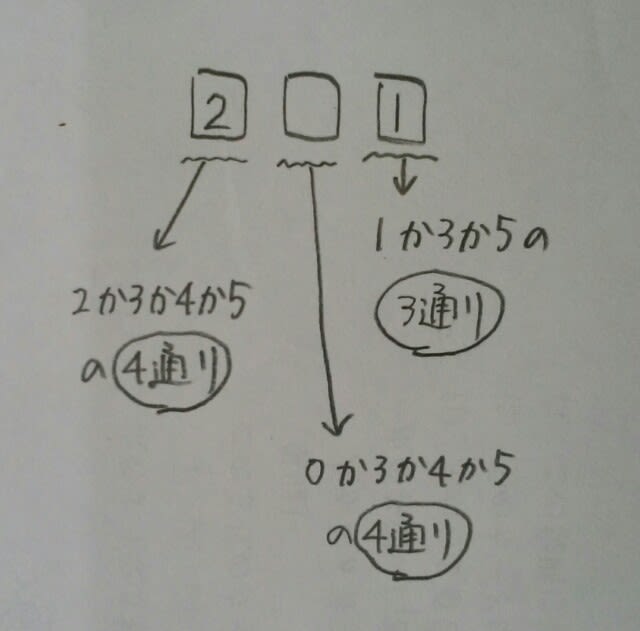よって、3×4×4＝48通り。 奇数以外はすべて偶数なので、偶数は、100－48＝52通り。ここをポチッとお願いします。→
選べる学習メディア LECの通信講座
今年（平成29年）の国家一般職（大卒）の問題です。 A～Gの七つのバレーボールチームがある。Aは、B～Gの六つのチームと1試合ずつ対戦することになっているが、過去の対戦成績から、Bに勝つ確率は1／3であり、その他のチームに勝つ確率はいずれも1／2であることが分かっている。このとき、Aが4勝以上する確率はいくらか。 ただし、試合には引き分けはないものとする。 ①7／24②3／8③11／24④13／24⑤5／8 Aは、Bとの対戦のときだけ勝つ確率が違うので、場合分けをします。図にすると、
まず、Bに勝つ場合は、
Bに負ける場合は、画像のイとウのときだから、5／32＋1／32＝6／32。
よって、
正解は、肢①です。ここをポチッとお願いします。→
【どこよりもお得なauひかりサイトはここ！】
練習問題です。 1個のサイコロを何回か振って、奇数の目が3回出たところでやめるようにするとき、ちょうど6回振ったところでやめることになる確率を求めよ。 6回振って、3回奇数の目が出るから……と考えた人は失敗します。 例えば、はじめの3回で、3回とも奇数の目が出てしまったら、そこでやめてしまうからです。 「6回振ったところでやめることになる」とは、「6回目に3回目の奇数の目が出てやめることになる」という意味です。 つまり、1～5回目で奇数の目が2回出ていて、6回目を振ると奇数の目が出る。と考えるのですね。よって、
計算すると、
正解は、5／32です。 もう1問やってみて下さい。 サイコロを5回投げたとき、ちょうど5回目で2回目の1の目が出る確率を求めよ。（正解は、動物画像の下） 次回、国家一般職（大卒）の問題を紹介します。 ここをポチッとお願いします。→
正解125／1944
