地方上級の判断推理 1

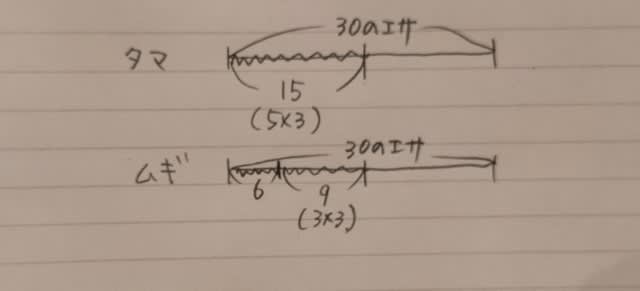
2021年出題。　　　　　　　　　　　　　　　　　　　夏休みにどこへ行ったかについて、「水族館に行った人は、映画館に行っていない」と言うためには、次のア〜オのうち2つが言えれば良い。それらはどれか。　　　　　　　　　　　　ア　映画館に行った人は、美術館に行かなかった。　　　　　　　　　　　　　　　　　　　　　　イ　水族館に行った人は、美術館に行かなかった。　　　　　　　　　　　　　　　　　　　　　　ウ　美術館に行った人は、映画館に行った。　　　　　　　　　　　　　　　　　　　　　エ　美術館に行った人は、水族館に行った。　　　　　　　　　　　　　　　　　　　　　　　オ　美術館に行かなかった人は、水族館に行かなかった。　　　　　　　　　　　　　　　　　①ア、イ②ア、エ③ア、オ④イ、ウ⑤ウ、オ　　　　　　　　　　　　　　　　　　　　　　　　　まずは、ア〜オの内容と、それぞれの対偶を書き出しておきます。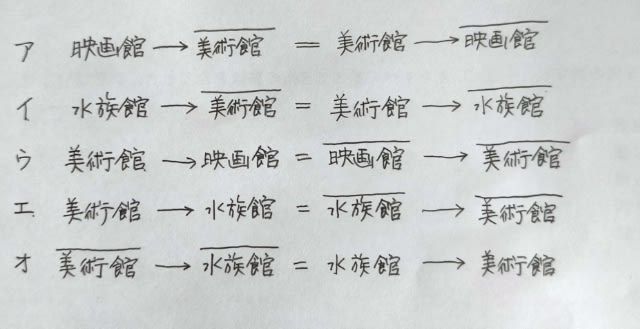
肢①アとイが言えた場合。　　　　　　　　　　　　　　　　水族館に行った人は美術館に行っていない。　　　　　　　　　　　　　　　　　　　　　　　　　　美術館に行っていない人がどうだったかは不明。　　　　　　　　　　　　　　　　　　　　　　肢②アとエが言えた場合。　　　　　　　　　　　　　　　　水族館に行った人がどうだったか不明。肢③アとオが言えた場合。　　　　　　　　　　　　　水族館に行った人は美術館に行っている（オの対偶）。　　　　　　　　　　　　　　　　　　　　　美術館に行った人は映画館に行っていない（アの対偶）。　　　　　　　　　　　　　　　　　　これが正解ですね。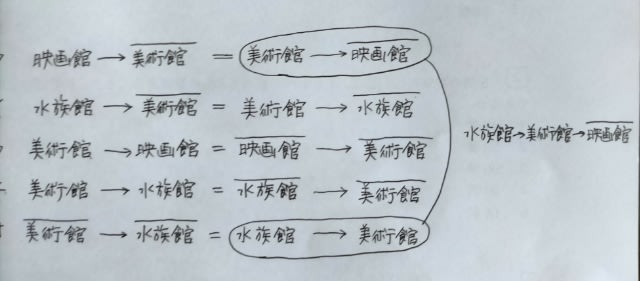
肢④イとウが言えた場合。　　　　　　　　　　　　　　水族館に行った人は美術館に行っていない。　　　　　　　　　　　　　　　　　　　　　　　美術館に行っていない人がどうだったかは不明。　　　　　　　　　　　　　　　　　　　　　肢⑤ウとオが言えた場合。　　　　　　　　　　　　　　水族館に行った人は美術館に行っている。　　　　　　　　　　　　　　　　　　　　　　美術館に行った人は映画館に行っている。　　　　　　　　　　　　　　　　　　　　　　　　これでは、水族館に行った人は映画館に行っていることになる。　　　　　　　　　　　　　　正解は肢③です。

地方上級の数的推理 6

2021年地方上級の第6問は、流水算でした。流速が一定の川があり、川の上流にP地点、下流にQ地点がある。静水を一定の速さで航行する船が、Q地点からP地点まで航行するのにかかった時間は、P地点からQ地点まで航行するのにかかった時間の5倍であった。静水における船の速さは、川の流速の何倍であったか。（選択肢省略）　　　　　　　　　　　　　　　　　　　　　①P地点からQ地点まで行こうが、Q地点からP地点まで行こうが、進む距離は同じ。　　　　　　　　　　　　　　　　　　　　②5倍の時間がかかったということは、進む速さは1/5。　　　　　　　　　　　　　　　　③静水での船の速さをx、川の流速をyとすると、P→Qの速さはx＋y。Q→Pの速さはx−y。①、②、③より、x＋y:x−y＝5:1。　　　　　　　　　　　　　　　　　　　　よって、5（x−y）＝x＋y。整理すると2x＝3y。ゆえにx:y＝3:2。



正解は、1.5倍です。　　　　　　　　　　　　　実は、本問のように、上りと下りの所要時間の比が分かっているときには、裏ワザがあります。

上りと下りの所要時間の比が5:1だから、静水での船の速さと川の流速は6:4。　　　　　　6÷4＝1.5だから、正解は1.5倍。　　　　　　　　暗算で正解が分かるのです。　　　　　　　　　　昨年、国家一般職でも、出ました。
選択肢②が正解ですね。
過物船
おちゃメンタル☆パーティー　藤宮ゆな

地方上級の数的推理 5

2021年地方上級の第5問は、仕事算と速さの融合問題でした。　　　　　　　　　　　　ある家では、タマとムギという2匹の猫を飼っており、同じ量の餌を、毎朝、それぞれお皿に入れて与えている。タマは6分で食べきり、ムギは10分で食べきる。ある朝、ムギに餌をあげてから2分後、タマにも餌をあげたとき、お皿に残っている餌の量が同じになるのは、タマに餌をあげてから何分後か。　　　　　　　　　　　　　ただし、2匹とも、自分のお皿の餌しか食べないこととし、餌がなくなるまでそれぞれが食べる速さを変えずに食べ続けるものとする。（選択肢省略）　　　　　　　　　　　　　　　　　　　　前半は仕事算ですね。　　　　　　　　　　　　　　　　このブログでは、仕事全体の量を1として考えるのではなく、仕事を終える時間の最小公倍数として考える解法を採用しています。　　　　　　　　　　　　　　　　　　　　6と10の最小公倍数は30ですから、餌の量を30とします。　　　　　　　　　　　　　　　　タマは、30の餌を6分で食べ切るので、1分で5食べる。　　　　　　　　　　　　　　　　　ムギは30の餌を10分で食べ切るので、1分で3食べる。　　　　　　　　　　　　　　　　　ここからは速さの問題ですね。　　　　　　　　　　ある朝、ムギに餌を与えて、その2分後にタマに餌を与えました。　　　　　　　　　　　　　このとき、ムギはすでに3×2＝6だけ食べています。　　　　　　　　　　　　　　　　　ここまでを図にしておきます。
さあ、早食い競争が始まります。　　　　　　　　　ムギは現在6だけリードしていますが、なにせ、タマより食べるのが遅いので、やがてタマに追いつかれるのは必定です。　　　　　　　　　　タマはムギよりも1分で2（5−3＝2）だけ多く食べちゃいます。　　　　　　　　　　　　ムギは、せっかく6だけリードしていても、毎分2ずつ差は縮まるので、3分後には追いつかれます。　　　　　　　　　　　　　　　　　　　　　　このとき、こうなってます。
どちらにも同じ量の餌を与えたのだから、食べた量が同じになったということは、残った量も同じ。　　　　　　　　　　　　　　本問は、「タマに餌をあげてから何分後か」と聞いているので、正解は3分後です。
おちゃメンタル☆パーティー　　下谷あゆ

地方上級の数的推理 4

2021年の地方上級、第4問は、割合からの出題でした。　　　　　　　　　　　　　　　　ある資格試験の受験者の人数は、55%が男性で45%が女性であった。受験者全体の75%が合格者で、不合格者のうち60%が男性であった。男性合格者と男性不合格者の人数の差が250人であったとき、女性合格者は何人か。（選択肢省略）　　　　　　　　　　　　　　　　　　合格か不合格か、男性か女性かを表にしますと、
合格者が75%なので、不合格者は25%。　　　　　　不合格者25%のうちの60%が男性だから、それは0.25×0.6＝0.15、すなわち15%です。
これで表は完成します。
男性合格者（40%）と男性不合格者（15%）の差が250人だから、25%が250人。　　　　　　　　　　　　　　　　　　　　よって、1%＝10人。　　　　　　　　　　　　　女性合格者は35%だから、350人。　　　　　　　　正解は、350人です。

地方上級の数的推理 3

2021年第3問も、方程式からの出題でしたが、どちらかというと、判断推理に近い内容です。　　　　　　　　　　　　　　　　　A、Bの2人が32枚ずつコインを持ち、2人でじゃんけんをして勝った方が負けた方のコインのちょうど半分をもらうというゲームを行った。何回かじゃんけんをした結果、コインの枚数はAが15枚、Bが49枚といずれも奇数となり、これ以上ゲームを続けることができなくなったため、ここでやめた。AがBに勝った回数は何回か。（選択肢省略）　　　　　　　　　1回目のじゃんけんでAが勝ったらこうなります。
負けた方は、コインが半分になってしまいます。　　　　　　　　　　　　　　　　　　　ということは、負けた人は、負ける前は、その2倍のコインを持っていたことになります。　　　　　　　　　　　　　ゲームをやめたとき、Aは15枚のコインを持っていたのだから、負ける前は30枚持っていたのです。　　　　　　　　　　　　　　　　えっ？Aが負けたかどうか分からないじゃないかって？　　　　　　　　　いいえ、分かります。

だって、Bが負けたらおかしいじゃないですか。二人は合わせて64枚のコインを奪いあっているのに、Bが負けていたとすれば、Bは負ける前に98枚持っていたことになるからです。
同様に考えていくと、こうなります。

Aは3勝しています。正解は、3回です。　　　　　♬じゃんけんしよ、じゃんけんしよ、真剣勝負ズルするな!♫