東京消防庁no20

下のグラフは、2007年から2011年までの新エネルギー（3電種）による発電供給量をまとめたものである。このグラフから判断できることとして、最も妥当なのはどれか。2007年の3電種の合計は、グラフより、600弱。2001年の合計は、1000弱だから、肢 1はダメ。2008年から2009年にかけて、廃棄物発電＋バイオマス発電は増えていないから、肢2もダメ。2007年と2011年を比べると、太陽光発電は、2倍以上増えている。風力発電は、約１.5倍。廃棄物発電＋バイオマス発電は、243÷216＝約1.12倍。よって、肢3が正解。肢4は、少し微妙で、太陽光発電は、2009年から2010年は、362÷263＝約1.38倍。2010年から2011年は、491÷362＝約1.36倍。2010年が最大。肢5。例えば、2008年の合計は636で、2009年の合計は719なので、719÷636＝約1.13となり約13％の伸びなのでダメ。

東京消防庁no19

下の表は、平成21年から25年までのある地域の主な出火原因別火災件数をまとめたものである。この表から判断できることとして、最も妥当なのはどれか。21年の合計は、441＋201＋104＋27＋77＝850件。25年の合計は、250＋177＋71＋46＋86＝630件。
もしも850件に対して2割減少したとすると、850×0.8＝680件。確かに2割以上減少しているので、肢1が正解。24年の合計は623、25年の合計は630で増加しているから、肢2はダメ。たばこにていては、24年から25年にかけて増加しているから、肢3もダメ。火遊びは、25年よりも23年のほうが多いから、肢4もダメ。23年から24年にかけて、天ぷら油とガスコンロ、レンジの順位が変わっているから肢5もダメです。
おもしろ日記ランキングへ

東京消防庁2類解答

間違っているところもあるかもしれませんが……　no8 ⑤ no9 ③ no10 ④ no11 ③ no12 ② no13 ① no14 ⑤ no15 ① no16 ④ no17 ② no18 ② no19 ⑤ no20 ④ no21 ② no22 ⑤ no35 ② no36 ② no37 ① no38 ⑤

東京消防庁no18

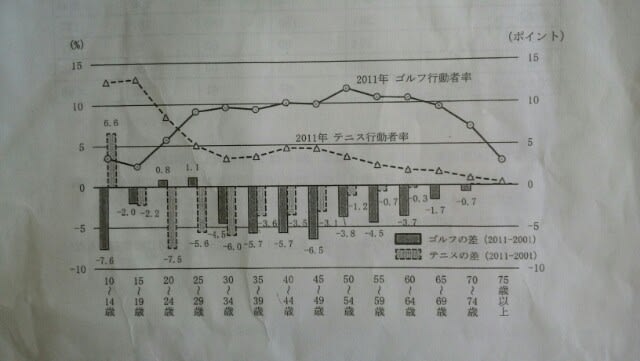
下のグラフは、折れ線グラフが、ゴルフとテニスを行う者の2011年の年齢階層別の比率を示しており、棒グラフは、年齢階層別の比率について2011年と2001年との差異（2011年－2001年）を示したものである。この図から判断できることとして、最も妥当なのはどれか。2011年については、折れ線グラフを見ればよいので、肢1と肢2は妥当ではない。　　　　　　　例えば、前回よりも5％減少したので、今回は60％だった。という話を聞けば、前回は65％だったと分かります。2011年は、60～64歳では、ゴルフはテニスの5.5倍。65～69歳では5倍近い。2001年は、60～64歳では、ゴルフは11＋3.7＝14.7％、テニスは2＋0.3＝2.3％だから6倍強。65～69歳では、ゴルフは9.5＋1.7＝11.2％、テニスは2％だから5.5倍程度。肢5が正解。

東京消防庁no17

1～5の番号が書かれた5つのボールを青色、赤色、黄色の3つの箱に入れる場合の数と、区別のつかない5つのボールを区別のつかない3つの箱に入れる場合の数の差として、最も妥当なのはどれか。ただし、5つのボールはすべて、いずれかの箱に入れるものとする。 1. 180 2. 197 3.204 4. 221 5.238 　　　　　　　　　　　　　　　すべての箱に最低1個はボールを入れるものとする、という問題はよくあるが、5つのボールはすべて、いずれかの箱に入れるものとする、という条件は、あまり見たことがありません。たとえば、①のボールはどの箱にも入れないなど、あまり考えたりしません。つまり、この条件は、「全てのボールは必ずどれかの箱に入れる」という、当たり前のことをいっているだけです。よって、この問題を考えるときには、空になる箱があってもあっても構わない。 前者は、重複順列なので、3の5乗で、243通り。（①は、青か赤か黄色かで3通り。②も、同様に3通り。③も④も⑤も3通り。その結果、空の箱ができても、こっちの知ったことではない。）後者は、何個入りの箱が何種類できるかだけを聞いています。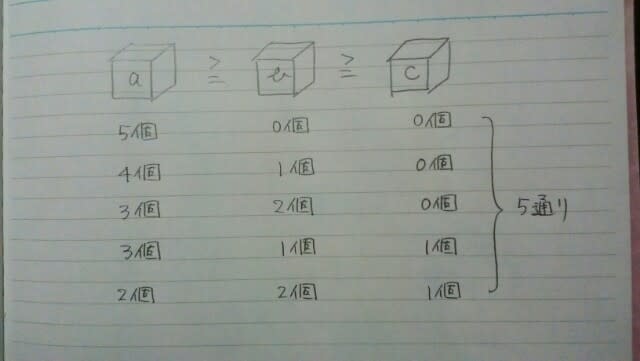一番多い箱をa,2番目に多い箱をb,一番少ない箱をc（同じ個数もあり）とすると、よって、その差は、243－5＝238通り。5が正解。