2021年出題。 平面において、一辺の長さが6cmである正六角形を、直線lに沿ってすべらないように1回転させたとき、正六角形の頂点Pが描く軌跡は下図の太線のようになった。 円周率をπとして、この軌跡の長さを①〜⑤から一つ選べ。ただし、直線lは動かないものとする。
①12πcm ②14πcm ③16πcm ④(8+4√3)πcm ⑤(12+4√3)πcm 公式があるので、あとで紹介しますね。 とりあえず、1回転がしましょう。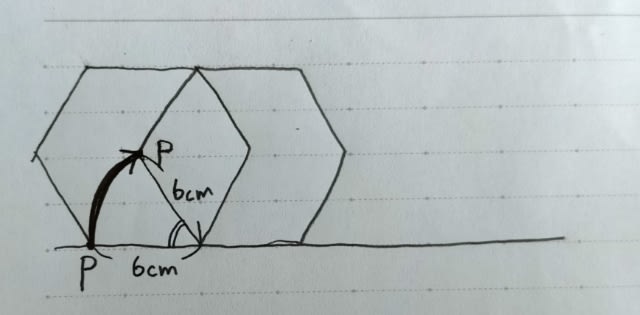
このとき、何が起こったのかというと、点Pは、60°回転したのです。 もう少し詳しく説明すると、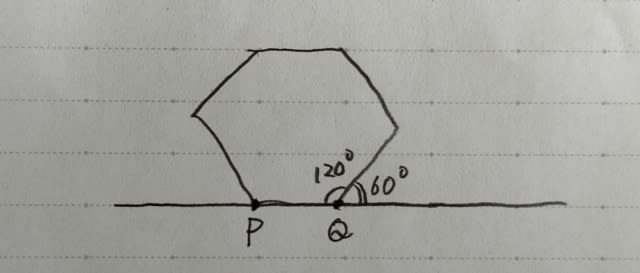
正六角形が右側に転がるとき、60°だけ回転すると直線lにべちゃっとくっついてしまいます。 正六角形が60°回転するのだから、点Pだって60°回転します。 回転の中心は点Qです。 つまり、点Pは、点Qを中心にして、60°回転します。その時の半径は6cm。 では、その次、
やはり、60°回転しますね。 ただ、このときの半径は6cmではありません。 6√3cmです。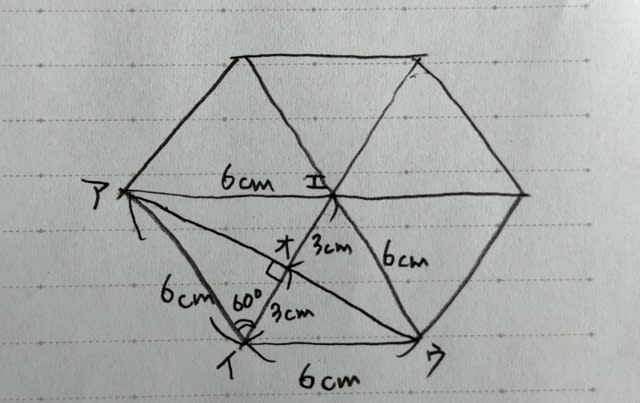
図で、四角形アイウエは、ひし形。 ひし形の対角線は直角に交わります。 三角形アイオは辺の長さが1:2:√3の三角定規だから、アオ=3√3。 よってアウ=6√3。 つまり、点Pは、点Rを中心にして、60°回転します。その時の半径は6√3cm。 その次。
60°回転。半径は12cm。 点Pは、点Sを中心にして、60°回転します。その時の半径は12cm。 その次。
60°回転。半径は6√3cm。2回目の回転と同じですね。 点Pは、点Tを中心にして、60°回転します。その時の半径は6√3cm。 最後。
60°回転。半径は6cm。1回目の回転と同じです。 点Pは、点Uを中心にして、60°回転します。その時の半径は6cm。 ピンク色の部分をすべてつなぎ合わせると、軌跡の長さが分かります。 一つ一つの長さを計算すると面倒なので、まとめます。 扇形の弧の長さは、2×半径×中心角/360でしたね。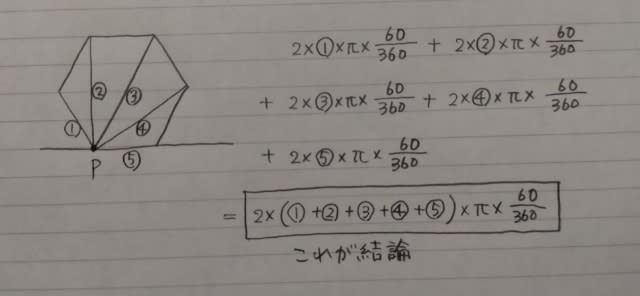
ということになり、一般化した公式は、
本問の場合は、点Pが正六角形の頂点にあるので、ただし書きのように、6−1=5つの長さを足して、2倍して、πをかけて、最後に60/360にすれば答えです。 やってみましょう。
正解は、肢④です。


①12πcm ②14πcm ③16πcm ④(8+4√3)πcm ⑤(12+4√3)πcm 公式があるので、あとで紹介しますね。 とりあえず、1回転がしましょう。

このとき、何が起こったのかというと、点Pは、60°回転したのです。 もう少し詳しく説明すると、

正六角形が右側に転がるとき、60°だけ回転すると直線lにべちゃっとくっついてしまいます。 正六角形が60°回転するのだから、点Pだって60°回転します。 回転の中心は点Qです。 つまり、点Pは、点Qを中心にして、60°回転します。その時の半径は6cm。 では、その次、

やはり、60°回転しますね。 ただ、このときの半径は6cmではありません。 6√3cmです。

図で、四角形アイウエは、ひし形。 ひし形の対角線は直角に交わります。 三角形アイオは辺の長さが1:2:√3の三角定規だから、アオ=3√3。 よってアウ=6√3。 つまり、点Pは、点Rを中心にして、60°回転します。その時の半径は6√3cm。 その次。

60°回転。半径は12cm。 点Pは、点Sを中心にして、60°回転します。その時の半径は12cm。 その次。

60°回転。半径は6√3cm。2回目の回転と同じですね。 点Pは、点Tを中心にして、60°回転します。その時の半径は6√3cm。 最後。

60°回転。半径は6cm。1回目の回転と同じです。 点Pは、点Uを中心にして、60°回転します。その時の半径は6cm。 ピンク色の部分をすべてつなぎ合わせると、軌跡の長さが分かります。 一つ一つの長さを計算すると面倒なので、まとめます。 扇形の弧の長さは、2×半径×中心角/360でしたね。

ということになり、一般化した公式は、

本問の場合は、点Pが正六角形の頂点にあるので、ただし書きのように、6−1=5つの長さを足して、2倍して、πをかけて、最後に60/360にすれば答えです。 やってみましょう。

正解は、肢④です。











