2021年出題。 ある鉄道の直線区間では、特急列車A、特急列車B、快速列車Cがそれぞれ一定の速さで並走しており、列車の全長はいずれも180mである。 Aは、Bに追いついてからBを追い越すまでに30秒かかる。 また、Bは、Cに追いついてからCを追い越すまでに20秒かかる。 このとき、Aは、Cに追いついてからCを追い越すまでに何秒かかるか。 ただし、「追いつく」とは、列車の前端が他の列車の後端と並ぶことを指し、「追い越す」とは、列車の後端が他の列車の前端と並ぶことを指す。(選択肢省略) 列車が列車を追い越すときは、速さを引きます。 本問で、AがBを追い越すときは、Aの方が速いので、(Aの速さ)から(Bの速さ)を引きます。 その引いた速さのことを、相対速度と言います。 簡単に言うと、仮にBが止まっているとしたら、Aは、その相対速度で走っていることになるということです。 AがBを追い越す場面を図で説明しますね。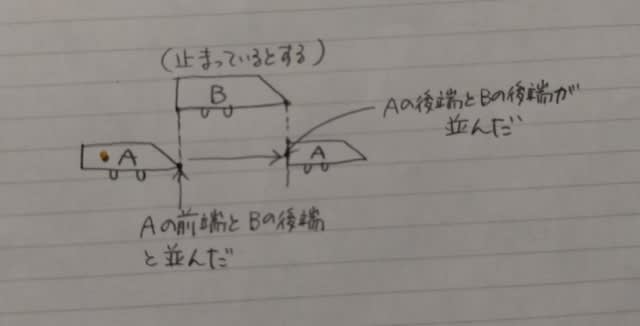
このとき、Aは、180+180=360m走っています。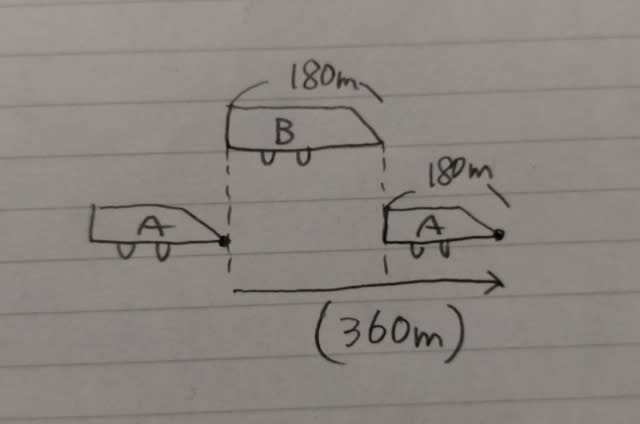
つまり、(列車の長さの和)だけ走っています。 かかった時間は30秒。 Aの速さをa(m/秒)、Bの速さをb(m/秒)、Cの速さをc(m/秒)とします。 AがBを追い越すときの相対速度は、a−b(m/秒)で、追い越すのに30秒かかっているので、
BがCを追い越すときの相対速度はb−c(m/秒)で、20秒かかっているので、
①+②をして、bを消去します。
a−c=10ということは、AがCを追い越すときの相対速度が30(m/秒)ということですね。 AがCを追い越すときの相対速度が30m/秒、進む距離は360mだから、360÷30=12秒かかります。 正解は、12秒です。 えっ、相対速度は嫌い〜? まあ、実際は走っているのにそれを止まっていると仮定してなどという発想は性に合わねえ!というお気持ち、理解できます。 そういう人は、このようにやりましょう!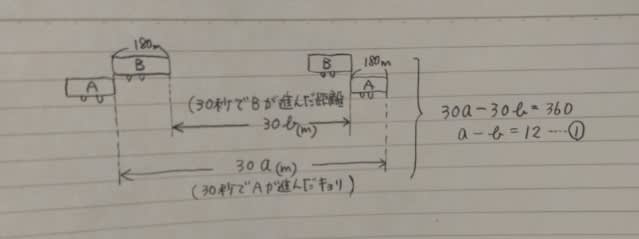




このとき、Aは、180+180=360m走っています。

つまり、(列車の長さの和)だけ走っています。 かかった時間は30秒。 Aの速さをa(m/秒)、Bの速さをb(m/秒)、Cの速さをc(m/秒)とします。 AがBを追い越すときの相対速度は、a−b(m/秒)で、追い越すのに30秒かかっているので、

BがCを追い越すときの相対速度はb−c(m/秒)で、20秒かかっているので、

①+②をして、bを消去します。

a−c=10ということは、AがCを追い越すときの相対速度が30(m/秒)ということですね。 AがCを追い越すときの相対速度が30m/秒、進む距離は360mだから、360÷30=12秒かかります。 正解は、12秒です。 えっ、相対速度は嫌い〜? まあ、実際は走っているのにそれを止まっていると仮定してなどという発想は性に合わねえ!というお気持ち、理解できます。 そういう人は、このようにやりましょう!













