問題再掲。次の図のようにxy平面上の原点Oに1枚のコインを置き、下の規則に従ってコインを動かすこととする。次の(1)、(2)の問いの答えとして最も適切なものを、下のA~Dから一つずつ選び、その記号を書け。 〈規則〉サイコロを1回投げ、 (ⅰ)1か2の目が出たらx軸の正の方向に1だけ進む。 (ⅱ)3~6の目が出たらy軸の正の方向に1だけ進む (1)サイコロを3回投げ、規則に従って連続して動かしたとき、コインが置かれている座標が(1, 2)である確率を求めよ。 A.2/9 B.4/27 C.4/9 D.2/27 (2)サイコロを5回投げ、規則に従って連続して動かしたとき、コインが置かれている座標を(a, b)とする。このとき、a>bである確率を求めよ。 A.17/81 B.7/243 C.1/2 D.64/81 (1)1か2の目がx回、3~6の目がy回出たとすると、規則ⅰ、ⅱより、コインは(x, y)に移動します。よって、コインが(1, 2)に移動するのは、1か2が1回、3~6が2回出たときです。3回の試行で、1か2が1回出る確率を求めればよいので、反復試行の公式が使える人は、
〈規則〉サイコロを1回投げ、 (ⅰ)1か2の目が出たらx軸の正の方向に1だけ進む。 (ⅱ)3~6の目が出たらy軸の正の方向に1だけ進む (1)サイコロを3回投げ、規則に従って連続して動かしたとき、コインが置かれている座標が(1, 2)である確率を求めよ。 A.2/9 B.4/27 C.4/9 D.2/27 (2)サイコロを5回投げ、規則に従って連続して動かしたとき、コインが置かれている座標を(a, b)とする。このとき、a>bである確率を求めよ。 A.17/81 B.7/243 C.1/2 D.64/81 (1)1か2の目がx回、3~6の目がy回出たとすると、規則ⅰ、ⅱより、コインは(x, y)に移動します。よって、コインが(1, 2)に移動するのは、1か2が1回、3~6が2回出たときです。3回の試行で、1か2が1回出る確率を求めればよいので、反復試行の公式が使える人は、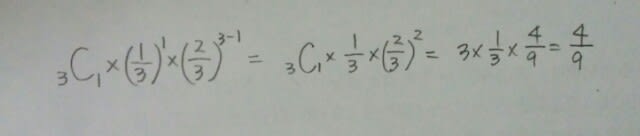 知らない人は、
知らない人は、 反復試行の公式って何?という人は、
反復試行の公式って何?という人は、 本問の場合は、3回やって、1回1か2の目が出る。として公式を使いました。えっ?3回やって2回3~6の目が出るってやったらだめかって?勿論構いません。
本問の場合は、3回やって、1回1か2の目が出る。として公式を使いました。えっ?3回やって2回3~6の目が出るってやったらだめかって?勿論構いません。 なんてったって、数学ほど自由なものはないのですから。正解は、Cです。 (2)5回投げますと、
なんてったって、数学ほど自由なものはないのですから。正解は、Cです。 (2)5回投げますと、 (5, 1)となる確率は、1/3の5乗で、1/243。(4, 1)となる確率は、
(5, 1)となる確率は、1/3の5乗で、1/243。(4, 1)となる確率は、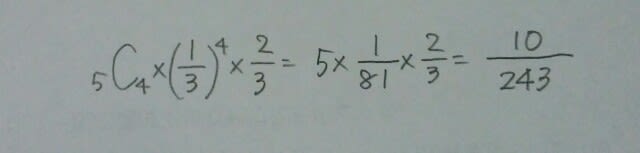 または、
または、 (3, 2)となる確率は、
(3, 2)となる確率は、 または、
または、 よって、求める確率は、
よって、求める確率は、 正解は、肢Aです。ここをポチッとお願いします。→
正解は、肢Aです。ここをポチッとお願いします。→


 〈規則〉サイコロを1回投げ、 (ⅰ)1か2の目が出たらx軸の正の方向に1だけ進む。 (ⅱ)3~6の目が出たらy軸の正の方向に1だけ進む (1)サイコロを3回投げ、規則に従って連続して動かしたとき、コインが置かれている座標が(1, 2)である確率を求めよ。 A.2/9 B.4/27 C.4/9 D.2/27 (2)サイコロを5回投げ、規則に従って連続して動かしたとき、コインが置かれている座標を(a, b)とする。このとき、a>bである確率を求めよ。 A.17/81 B.7/243 C.1/2 D.64/81 (1)1か2の目がx回、3~6の目がy回出たとすると、規則ⅰ、ⅱより、コインは(x, y)に移動します。よって、コインが(1, 2)に移動するのは、1か2が1回、3~6が2回出たときです。3回の試行で、1か2が1回出る確率を求めればよいので、反復試行の公式が使える人は、
〈規則〉サイコロを1回投げ、 (ⅰ)1か2の目が出たらx軸の正の方向に1だけ進む。 (ⅱ)3~6の目が出たらy軸の正の方向に1だけ進む (1)サイコロを3回投げ、規則に従って連続して動かしたとき、コインが置かれている座標が(1, 2)である確率を求めよ。 A.2/9 B.4/27 C.4/9 D.2/27 (2)サイコロを5回投げ、規則に従って連続して動かしたとき、コインが置かれている座標を(a, b)とする。このとき、a>bである確率を求めよ。 A.17/81 B.7/243 C.1/2 D.64/81 (1)1か2の目がx回、3~6の目がy回出たとすると、規則ⅰ、ⅱより、コインは(x, y)に移動します。よって、コインが(1, 2)に移動するのは、1か2が1回、3~6が2回出たときです。3回の試行で、1か2が1回出る確率を求めればよいので、反復試行の公式が使える人は、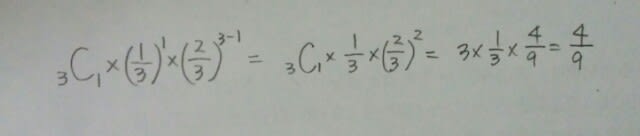 知らない人は、
知らない人は、 反復試行の公式って何?という人は、
反復試行の公式って何?という人は、 本問の場合は、3回やって、1回1か2の目が出る。として公式を使いました。えっ?3回やって2回3~6の目が出るってやったらだめかって?勿論構いません。
本問の場合は、3回やって、1回1か2の目が出る。として公式を使いました。えっ?3回やって2回3~6の目が出るってやったらだめかって?勿論構いません。 なんてったって、数学ほど自由なものはないのですから。正解は、Cです。 (2)5回投げますと、
なんてったって、数学ほど自由なものはないのですから。正解は、Cです。 (2)5回投げますと、 (5, 1)となる確率は、1/3の5乗で、1/243。(4, 1)となる確率は、
(5, 1)となる確率は、1/3の5乗で、1/243。(4, 1)となる確率は、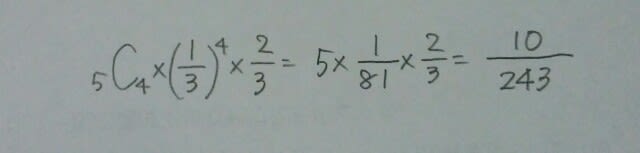 または、
または、 (3, 2)となる確率は、
(3, 2)となる確率は、 または、
または、 よって、求める確率は、
よって、求める確率は、 正解は、肢Aです。ここをポチッとお願いします。→
正解は、肢Aです。ここをポチッとお願いします。→










