2021年出題。 A〜Eの5人は、放課後にそれぞれ習い事をしている。 5人は、生け花教室、茶道教室、書道教室、そろばん教室、バレエ教室、ピアノ教室の六つの習い事のうち、Eは二つ、それ以外の人は三つの教室に通っている。 次のことが分かっているとき、確実にいえることとして最も妥当なのはどれか。 ○生け花教室に通っているのは4人、茶道教室は3人、書道教室は1人である。 ○AとCが共に通っている教室はない。 ○BとDが共に通っている教室は一つ、AとBが共に通っている教室は二つである。 ○BとEが共に通っている教室は一つ、AとEが共に通っている教室は二つである。 ○Cは、バレエ教室には通っていない。 ○Dは、そろばん教室に通っているが、ピアノ教室には通っていない。 ①Aは、生け花教室とそろばん教室に通っている。 ②Bは、茶道教室と書道教室に通っている。 ③Cは、そろばん教室とピアノ教室に通っている。 ④Dは、茶道教室とバレエ教室に通っている。 ⑤Eは、生け花教室とバレエ教室に通っている。 条件を表にすると、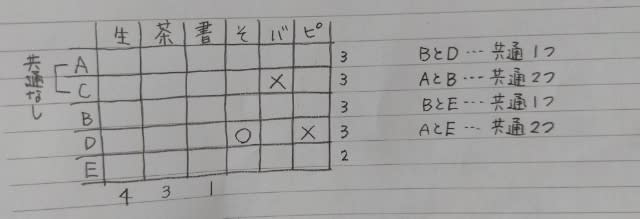
(AとCは共通なしなので、AとCが隣り合うように表を作っています。) AとCは、共通なしで、3つずつだから、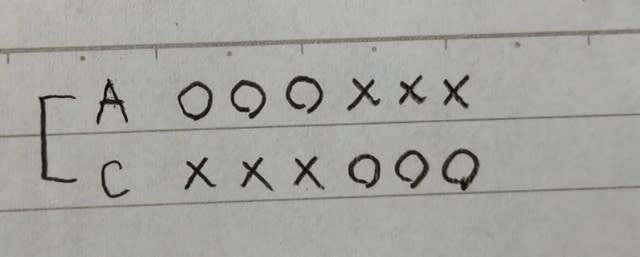
つまり、6つの習い事全て、AかCのどちらか一人が通っています。 よって、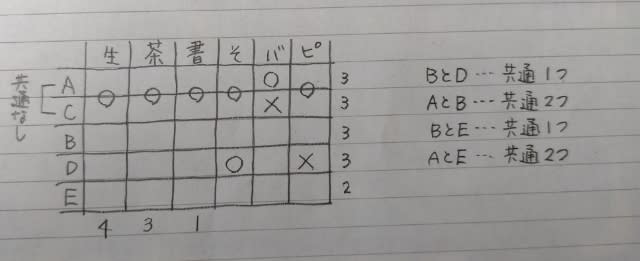
生け花4人、書道1人だから、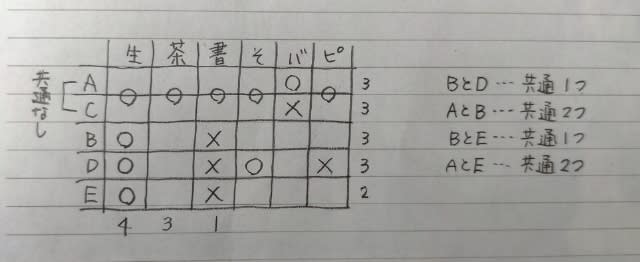
条件に、BとDは共通1つというのがあります。 今、BとDは生け花が共通しています。 そこで、仮にEが、茶道なんか習いたくない!と言い出したらどうなるでしょうか? BとDの共通がもう一つ増えてしまいますね。 だから、Eは茶道教室に通わなければいけません。 よって、Eは生け花と茶道教室に通い、習い事の王道を歩みます。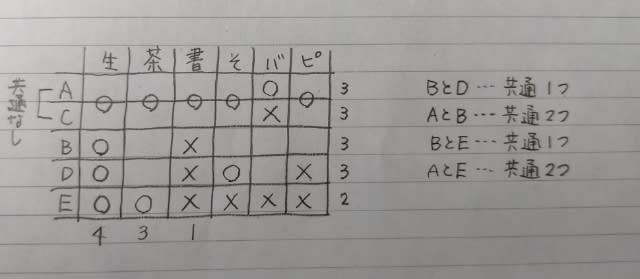 ここで肢⑤はダメ。
ここで肢⑤はダメ。
BとDの共通は1つなので、Bは、そろばん教室には通っていません。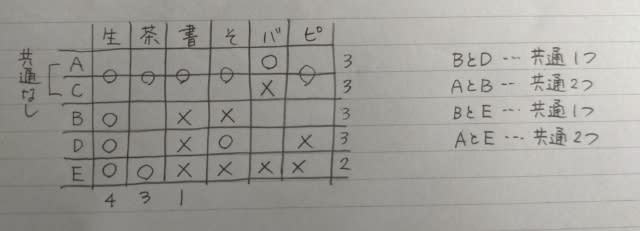
AとEの共通が2つということは、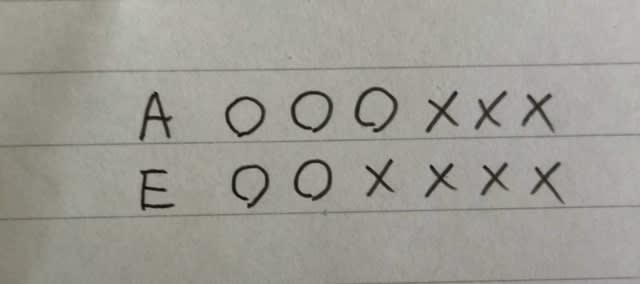
Eが通っている2つの教室には、必ずAも通っているということ。 よって、Aは生け花、茶道、バレエ教室に通っています。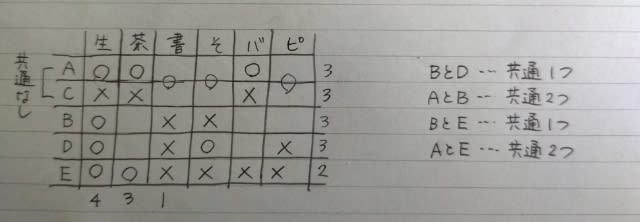
じゃあ、Cは書道、そろばん、ピアノ教室ですね。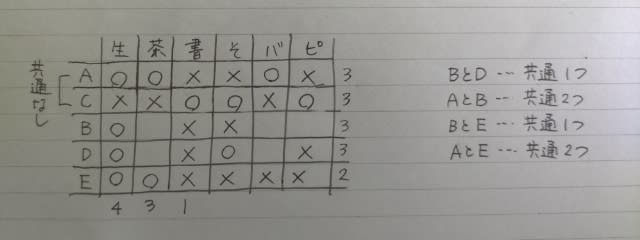
ここまでで、正解は、肢③と決定します。 BとEの共通は1つだから、Bは茶道教室には通っていない。 よって、Bは生け花、バレエ、ピアノです。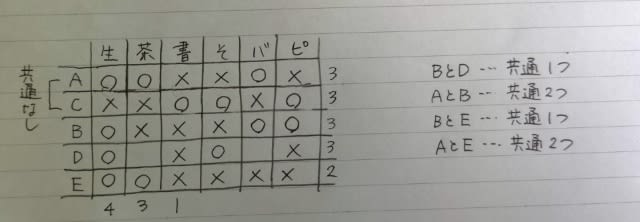
BとDの共通は1つだから、Dはバレエ教室には通っていない。 よって、Dは生け花、茶道、そろばんです。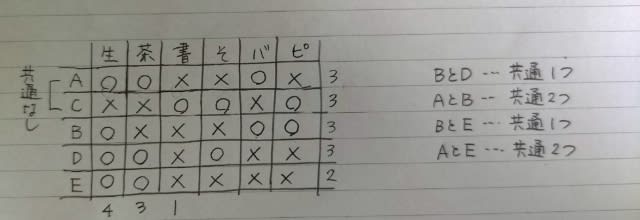

幼児期
学生時代
現在
未来

(AとCは共通なしなので、AとCが隣り合うように表を作っています。) AとCは、共通なしで、3つずつだから、
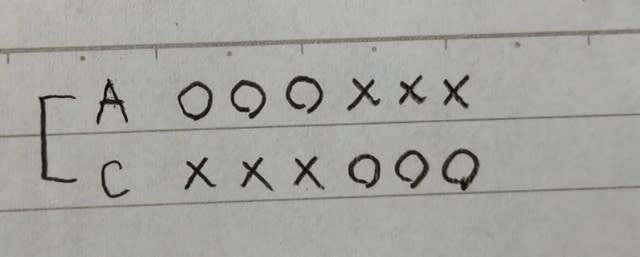
つまり、6つの習い事全て、AかCのどちらか一人が通っています。 よって、

生け花4人、書道1人だから、

条件に、BとDは共通1つというのがあります。 今、BとDは生け花が共通しています。 そこで、仮にEが、茶道なんか習いたくない!と言い出したらどうなるでしょうか? BとDの共通がもう一つ増えてしまいますね。 だから、Eは茶道教室に通わなければいけません。 よって、Eは生け花と茶道教室に通い、習い事の王道を歩みます。
 ここで肢⑤はダメ。
ここで肢⑤はダメ。BとDの共通は1つなので、Bは、そろばん教室には通っていません。

AとEの共通が2つということは、
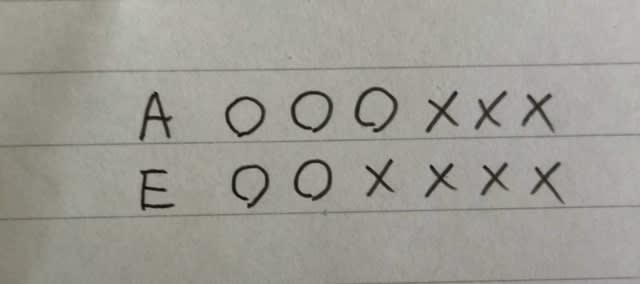
Eが通っている2つの教室には、必ずAも通っているということ。 よって、Aは生け花、茶道、バレエ教室に通っています。

じゃあ、Cは書道、そろばん、ピアノ教室ですね。

ここまでで、正解は、肢③と決定します。 BとEの共通は1つだから、Bは茶道教室には通っていない。 よって、Bは生け花、バレエ、ピアノです。

BとDの共通は1つだから、Dはバレエ教室には通っていない。 よって、Dは生け花、茶道、そろばんです。


幼児期

学生時代

現在

未来





















※コメント投稿者のブログIDはブログ作成者のみに通知されます