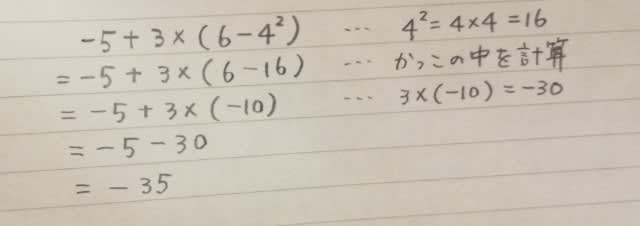1辺2cmの立方体について、下図のように頂点Aと辺の中点B、Cをとる。点A、B、Cを通る平面でこの立方体を切断するとき、切断面としてできる図形の周の長さはいくらか。1〜5から一つ選べ。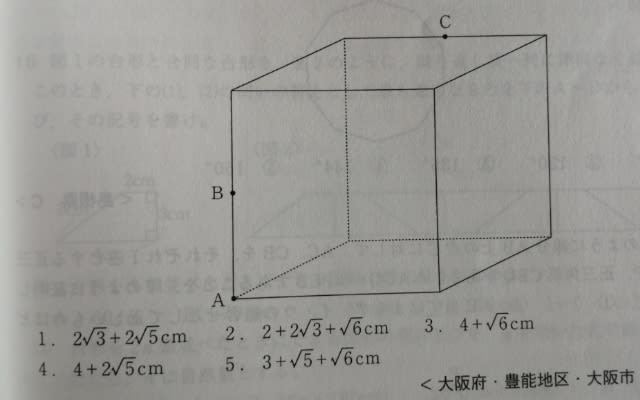
切断の基本は、次の二つです。 ①同じ平面上の2点を見つけ、まっすぐ結ぶ。(同じ平面上ではない2点を結ぶと、そこでゲームオーバー) ②平行な面を見つけ、平行な線を書き入れる。 カテゴリー「切断」に、本問と同じような記事が数個ありますので、参考にしていただければ。 さて、本問では、点Aと点Bは同じ面上にありますので、まっすぐ結びます。AとC、BとCは違う面上にあるので、決して結んではいけません。すると、
AとBを結ぶと、Dにたどり着きました。この点DとCは同じ平面上にあるので、結びます。
CとAを結んで、終わりにしたい気持ちは分かりますが、CとAは違う平面上にあるので、まだダメ。 今度は、平行な面を探します。 探すと言っても、上の面と下の面が平行なのは当たり前ですから、下の面に、上の面の切り口と平行に線を引きます。
CとEは同じ平面上にあるので、結んで出来上がりです。
な〜にをくどくどとやってるんざ〜ますか〜。 立方体の形をした羊羹があって、AとBに包丁を当てて、そのままCに向かって切って見れば、すぐに分かるざ〜ますわ!などと言うなかれ。 なるほどこの一問に限って言えばその通りなのですが、もっと複雑な立体の切断を考えるときに用いる方法です。 ただし、曲面の切断にはこれは通用しません。さて、周の長さは、
2+√5+2+√5=4+2√5(cm)で、正解は、肢4です。ここをポチッとお願いします。→
にほんブログ村


切断の基本は、次の二つです。 ①同じ平面上の2点を見つけ、まっすぐ結ぶ。(同じ平面上ではない2点を結ぶと、そこでゲームオーバー) ②平行な面を見つけ、平行な線を書き入れる。 カテゴリー「切断」に、本問と同じような記事が数個ありますので、参考にしていただければ。 さて、本問では、点Aと点Bは同じ面上にありますので、まっすぐ結びます。AとC、BとCは違う面上にあるので、決して結んではいけません。すると、

AとBを結ぶと、Dにたどり着きました。この点DとCは同じ平面上にあるので、結びます。

CとAを結んで、終わりにしたい気持ちは分かりますが、CとAは違う平面上にあるので、まだダメ。 今度は、平行な面を探します。 探すと言っても、上の面と下の面が平行なのは当たり前ですから、下の面に、上の面の切り口と平行に線を引きます。

CとEは同じ平面上にあるので、結んで出来上がりです。

な〜にをくどくどとやってるんざ〜ますか〜。 立方体の形をした羊羹があって、AとBに包丁を当てて、そのままCに向かって切って見れば、すぐに分かるざ〜ますわ!などと言うなかれ。 なるほどこの一問に限って言えばその通りなのですが、もっと複雑な立体の切断を考えるときに用いる方法です。 ただし、曲面の切断にはこれは通用しません。さて、周の長さは、

2+√5+2+√5=4+2√5(cm)で、正解は、肢4です。ここをポチッとお願いします。→
にほんブログ村
















 でも、「50 までの自然数の中にに含まれる素数を全て足すといくらか?」などという鬼👹問題が出たらどうしましょう?実際にあったと思います。 普段数学に親しんでいる者ならば、普通にやれますが、慣れていない人にとってはまさに👹問題ですね。 「エラトステネスのふるい」というものがあります。まず、1から50まで順番に数字を並べます。
でも、「50 までの自然数の中にに含まれる素数を全て足すといくらか?」などという鬼👹問題が出たらどうしましょう?実際にあったと思います。 普段数学に親しんでいる者ならば、普通にやれますが、慣れていない人にとってはまさに👹問題ですね。 「エラトステネスのふるい」というものがあります。まず、1から50まで順番に数字を並べます。