よって、
よって、
 ゆえに、もとの数は、865。というのが、普通の解法ですが、本問は、選択肢に、もとの数が書いてあるので、まず、全ての選択肢が、確かに「それぞれの位の数の和は19」という条件をクリアーしていることを確かめた上で、
ゆえに、もとの数は、865。というのが、普通の解法ですが、本問は、選択肢に、もとの数が書いてあるので、まず、全ての選択肢が、確かに「それぞれの位の数の和は19」という条件をクリアーしていることを確かめた上で、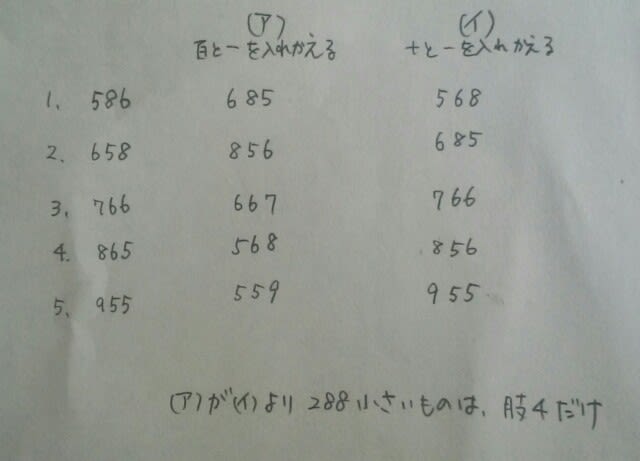 とした方が、楽ですねえ。
とした方が、楽ですねえ。


500円以内でチョコレートとガムを買いに行く。チョコレートは1個30円、ガムは1個110円である。チョコレートもガムも必ず1個は買うとき、500円以内で買うことができるチョコレートとガムの個数の組合せは全部で何通りあるか。最も適切なものを、次の①~⑤のうちから選びなさい。ただし、消費税は考えないこととする。 ①25通り②29通り③31通り④47通り⑤51通りどちらも最低1個は買うので、先に1個ずつ買っておくと、30+110=140円かかり、あと360円以内です。チョコレートをx個、ガムをy個買うとすると、30x+110y≦360 両辺を10で割って、3x+11y≦36

 よって、13+9+5+2=29通りで、肢②が正解です。
よって、13+9+5+2=29通りで、肢②が正解です。



 よって、13+9+5+2=29通りで、肢②が正解です。
よって、13+9+5+2=29通りで、肢②が正解です。

次に、式を使ったやり方。

 少なくとも1回は勝ったのだから、y≧1。よって、
少なくとも1回は勝ったのだから、y≧1。よって、 また、ジャンケンは16回したのだから、
また、ジャンケンは16回したのだから、 ゆえに、負けた回数は、14回以上、14回以下だから、14回です。正解は、肢③です。
ゆえに、負けた回数は、14回以上、14回以下だから、14回です。正解は、肢③です。

ある果物屋で、1個120円のりんごと、1個450円のパイナップルをそれぞれいくつか購入し、代金として12600円を支払った。このとき、2種類の果物の個数の選び方は何通りあるか。ただし、商品の値段には消費税が含まれているものとする。 ①6通り②8通り③10通り④12通り⑤14通り オーソドックスな、不定方程式の問題です。りんごをx個、パイナップルをy個買ったとして、方程式を作ると、120x+450y=12600です。このあと、式を変形します。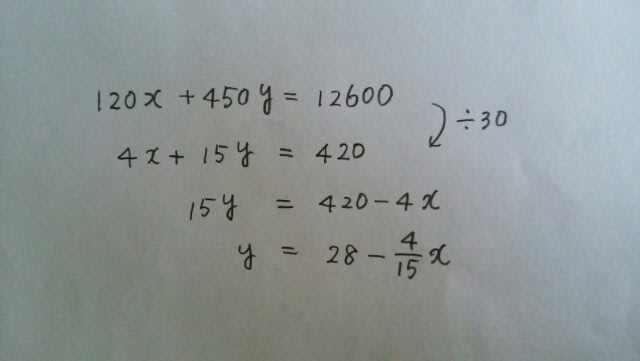 例えば、xが20だったとします。xに20を代入すると、yは、3分の68となって、パイナップルを3分の68個買うことになります。そんなことはできません。つまり、xもyも、買った果物の個数だから、整数(負の整数は除く)です。よって、xは、15の倍数でなければいけませんね。
例えば、xが20だったとします。xに20を代入すると、yは、3分の68となって、パイナップルを3分の68個買うことになります。そんなことはできません。つまり、xもyも、買った果物の個数だから、整数(負の整数は除く)です。よって、xは、15の倍数でなければいけませんね。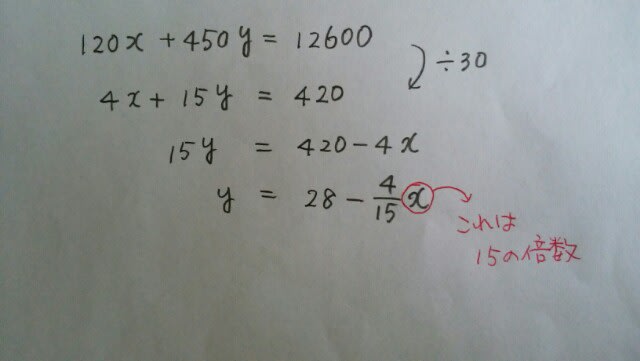 また、問題文中には、「ただし、どちらの果物も、最低1個は買うものとする」とは書いてないので、xやyが、0
また、問題文中には、「ただし、どちらの果物も、最低1個は買うものとする」とは書いてないので、xやyが、0
になっても構いません。 もしも、xが0だったら、yは28。xが15だったら、yは24……これを、表にします。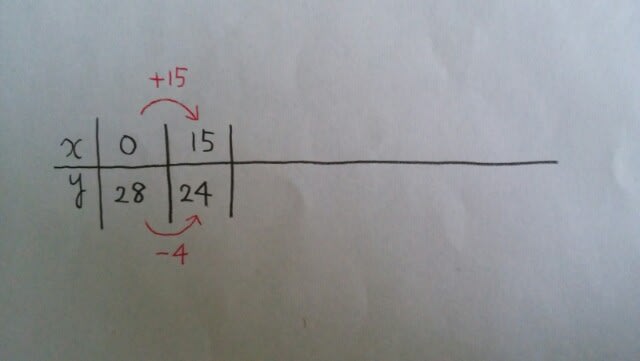 xが15増えると、yは4ずつ減っていきます。このまま表を続けていくと、
xが15増えると、yは4ずつ減っていきます。このまま表を続けていくと、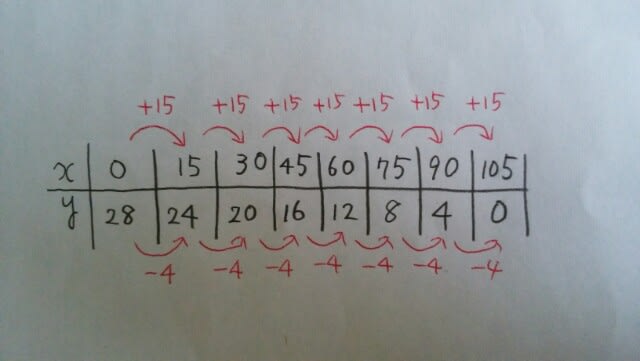 本問の場合は、何通りあるかを答えるだけなので、xのところは空欄にしておいて、yだけ記入していけばよいのです。表より、8通りの買い方があるのが分かります。正解は肢②です。
本問の場合は、何通りあるかを答えるだけなので、xのところは空欄にしておいて、yだけ記入していけばよいのです。表より、8通りの買い方があるのが分かります。正解は肢②です。
にほんブログ村

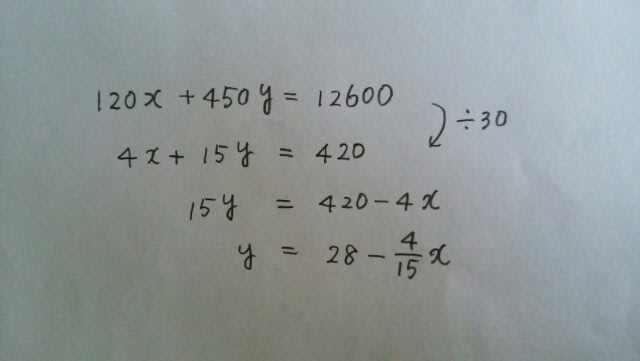 例えば、xが20だったとします。xに20を代入すると、yは、3分の68となって、パイナップルを3分の68個買うことになります。そんなことはできません。つまり、xもyも、買った果物の個数だから、整数(負の整数は除く)です。よって、xは、15の倍数でなければいけませんね。
例えば、xが20だったとします。xに20を代入すると、yは、3分の68となって、パイナップルを3分の68個買うことになります。そんなことはできません。つまり、xもyも、買った果物の個数だから、整数(負の整数は除く)です。よって、xは、15の倍数でなければいけませんね。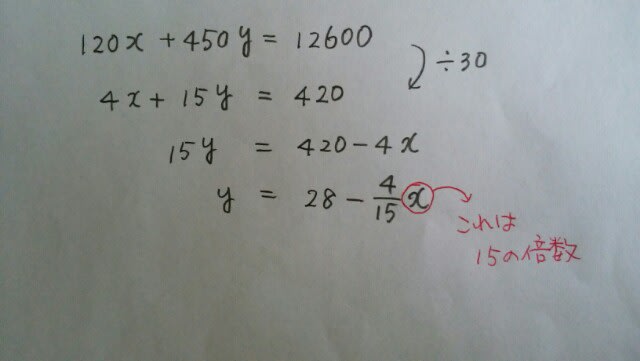 また、問題文中には、「ただし、どちらの果物も、最低1個は買うものとする」とは書いてないので、xやyが、0
また、問題文中には、「ただし、どちらの果物も、最低1個は買うものとする」とは書いてないので、xやyが、0になっても構いません。 もしも、xが0だったら、yは28。xが15だったら、yは24……これを、表にします。
 xが15増えると、yは4ずつ減っていきます。このまま表を続けていくと、
xが15増えると、yは4ずつ減っていきます。このまま表を続けていくと、 本問の場合は、何通りあるかを答えるだけなので、xのところは空欄にしておいて、yだけ記入していけばよいのです。表より、8通りの買い方があるのが分かります。正解は肢②です。
本問の場合は、何通りあるかを答えるだけなので、xのところは空欄にしておいて、yだけ記入していけばよいのです。表より、8通りの買い方があるのが分かります。正解は肢②です。にほんブログ村












 これをまとめると、
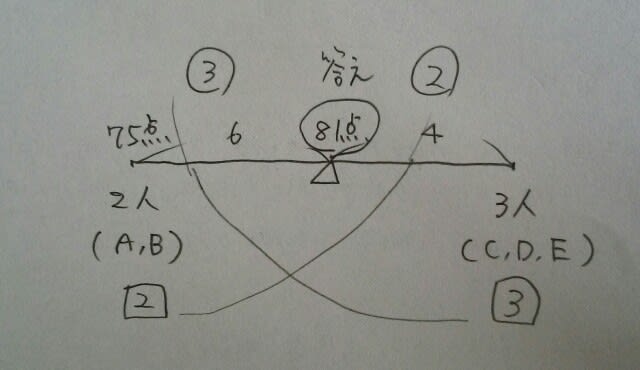
これをまとめると、 正解は、肢⑤です。また、AとBの平均は75点なので、てんびんで考えることもできますねぇ。
正解は、肢⑤です。また、AとBの平均は75点なので、てんびんで考えることもできますねぇ。