前回の3ビットグレイコードの続きで、いよいよ4ビットの話です。
第3章 4ビットグレイコード
3.1 グレイコード生成とハミルトン路問題
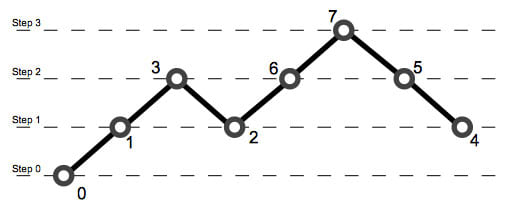
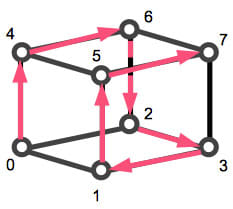
3ビットグレイコードの生成は、下図のような配置の7つの点を7回の移動で辿ることと同じでした。

これは、「一筆書き」と似ていますが、ちょっと違います。一筆書きは、全ての「辺」をダブることなく辿っていくことであるのに対し、この問題は、全ての「点」をダブることなく辿ることで、これは「巡回セールスマン問題(Traveling Salesman Problem)」において、辺の重み付けをなくした「ハミルトン路問題」(Hamilton Path Problem)と呼ばれます。
前回の説明で、3ビットグレイコードには、「循環型」と「非循環型」があることを示しましたが、「循環型」の場合は、特に「ハミルトン閉路問題」に分類されるようです。
「巡回セールスマン問題」にせよ、「ハミルトン路問題」にせよ、いろんな数、いろんな配置の「点」を、さまざまな「辺」で結んだものを、統一的に解く方法は見い出されていないようです。
コンピューターが得意とする「しらみつぶし法」も、「点」や「辺」の数が増えるほど、現実的な時間内に答えを得られない(例えば、4ビットの場合では21兆通りを調べる必要がある)ことが、人々の興味を惹くところです。
しかし、グレイコードに限っては、「点」と「点」の繋ぎ方に特徴があるため、どうやら解くことができそうです。
3.2 アップダウン法による3ビットグレイコードの生成
3ビットの場合、0~7の8つの数字を表します。8つの数字を表すので、少なくとも7回はビットを変化させなくてはなりません。1回の変化において1ビットしか変更しないなら、それはグレイコードです。
前述の図解は、1回の変化で1ビットしか変化しないで繋がる数字同士を辺で結んでいるので、この図を辿っていけば、自ずとグレイコードが得られます。
上図には、補助線として「Step 0」~「Step 3」を描いてあります。「点0」(Step 0上にある)からスタートして、7回進むと(7は奇数なので)「Step 1」か「Step 3」で終わることになります。「Step 1」で終わるということは「点1」「点2」「点4」で終わることなので「循環型」を示していて、「Step 3」は「点7」なので「非循環型」になるというわけです。
「Step 0」からスタートする場合、「Step 3」上の「点7」は1回しか通らないので、他の点とはちょっと違います。そこで、何回目に「点7」を通るかで整理してみます。「Step 3」は奇数回目にしか到達しません。奇数回目ということは、1回目、3回目、5回目、7回目のいずれかです。しかし、「点0」から「点7」へは少なくとも3回は要するので、3回目、5回目、7回目のいずれか、ということになります。
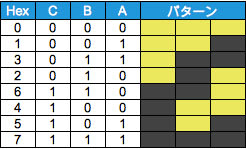
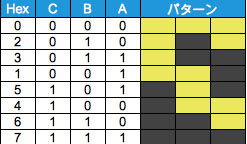
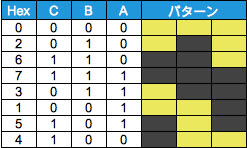
これは、前回の黄表で、それぞれ「3回目の移動で点7に到達」する循環型(左列)、「5回目の移動で点7に到達」する鏡像解(中央列)、「7回目の移動で点7に到達」する非循環型(右列)に相当します。
それぞれの移動例を示すと、下図(a)~(c)の3パターンになります(ちなみに、図(a)と図(b)が左右対称になっていて、お互いに鏡像関係になっていることが視覚化されています)。

図(a) 3回目に点7に到達
図(b) 5回目に点7に到達

図(c) 7回目に点7に到達
黄表で示した通り、この3パターンが得られれば、あとはビットの入替えですべての変種を得ることができます。3ビットの入替えによって得られる変種の数は、それぞれについて、3P3=3!=6通りなので、計18種類の配列が得られ、これは前回までに得られた結論と同様です。
あるいは、別の説明として、例えば、図(a)のパターンに対しては、はじめの動きでは点1、点2、点4の3通りの選択肢があり、このとき点1に進めば、次は、点3か点5の2通りの選択肢、ここで点3に進めば、あとは選択の余地なく終点まで進みます。したがって、3×2=6通り、ということで、前述の数字と一致します。
3.3 アップダウン法による4ビットグレイコードの生成
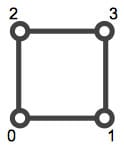
2ビットのときは二次元の正方形、3ビットのときは三次元の立方体を用いると便利だったのですが、4ビットでは四次元になってしまうので、ドラえもんに頼まない限り、私たちには見ることができません。とはいえ、3ビットのときと同じような絵柄で解くことができます。
具体的には、4ビットグレイコードの場合、前述の3ビットの図を2つ並べたような感じになります。左下の立方体のような塊は3ビットのときと同じ図で、右上の立方体と、それぞれの頂点が繋がっています。3ビットではA極からC極の3ビットでしたが、4ビットではD極が加わります。左下の立方体はD極が0、右上の立方体はD極が1の状態に相当します。
四次元的に言うならば、左下と右上の立方体は異なる時間に存在するとか、両者はパラレルワールドに存在する、とか、どんな風に考えるも自由です。
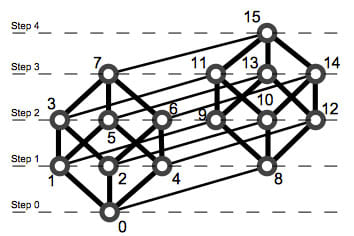
4ビットグレイコードでは、0~Fの16通りの数字を示すので、15回の移動ですべての点を巡る必要があります。15は奇数なので、点0の「Step 0」からスタートすると、15回目には「Step 1」か「Step 3」で終点を迎えます。終点がStep 1上であれば「循環型」、Step 3ならば「非循環型」になります。
Step 4上の点15は1回しか通らないので、そこに着目して、3ビットのときと同様に移動パターンを整理してみます。Step 4に到達するのは、4回目以降の偶数回目ですから、4回目、6回目、8回目、10回目、12回目、14回目のいずれかです。それぞれのパターン(の一例)を描いてみると、図(a)~図(f)の6通りです。このうち、(a)と(e)、(b)と(d)は鏡像関係にあります。したがって、この後は、(a)、(b)、(c)、(f)について調べていくことにします。

図(a) 4回目に点15に到達

図(b) 6回目に点15に到達

図(c) 8回目に点15に到達

図(d) 10回目に点15に到達

図(e) 12回目に点15に到達

図(f) 14回目に点15に到達
まず、(a)のパターンですが、「4回目に点15に到達」するパターンは、この他にもあり、全部で5C2=10通りがあります。実際に、これらのパターンで、下図の道筋(前掲と同じ)で全てのノードを辿ることができるかどうかを検証する必要があります。

ちょっと、ややこしくなってきました





























































 『天球の歩き方 総集編』は
『天球の歩き方 総集編』は