算額のうち、立体の問題を解いてみました。道後八幡「伊佐爾波神社」に、大西佐兵衛が享和3年(1803年)に奉納した算額です。
まず、下図のような見慣れない形状の容器が登場します。この形は「弧環減球」と呼ばれています。

この容器の中に、2つの中球と1つの小球が、ぴったりと収まっています。中球の直径が3寸、小球の直径が2寸のとき、容器と3つの球の間に残る空隙の体積はいくらか、というのが問題です。

1.弧環減球って、どんな形なのか
まず、「弧環減球」なるものを理解するのに手間取りました。下図は、鉛直中央断面です。

「弧環」というのは、円弧を中心軸の周りにくるっと一回りさせて出来るものを指すようです。はじめ、「弧環」という名称から、涼麻父は「上面と底面は、それぞれ独立した別々の円弧の場合もあり得る」と考えたのですが、結論から言うと、上面も底面も同一の円弧のようです。つまり、下図の黄色の円をくるっと一回りさせたときに出来上がる球面です。

となると、黄色の円の直径は青色の直径と赤色の直径2つ分の和です。ここで、それぞれの円の半径を、青色r1、赤色r2、黄色r3とします(直径でも良いのですが、現代数学では半径で考えることが多いので)。黄色の半径r3は次式で表されます。


次に「減球」ですが、これは、ときどき登場する用語で、側面を円弧で削り込んだ形のことです。木地をろくろ挽きするイメージでしょうかね。下図でいうと、黄色の球体をくるくるっと回しながら、緑色の円弧で削り落とす感じです。

このとき、緑色の円の半径をr4とすると、ピタゴラスの定理から次式が得られます。


それにしても「弧環減球」という呼び名は曖昧&曲者で、理解するまでに一苦労。実は、この問題で一番の難関です。結果から言えば、「弧環減球」は、外観がリンゴ を丸かじりした後に残った芯のような形を指すようです。
を丸かじりした後に残った芯のような形を指すようです。

2.解いてゆく
容器の体積を求めて、そこから2つの中球と1つの小球の体積を差し引けばよいので、まずは、容器の体積を求めます。容器の体積は、上蓋+胴部+底蓋(=上蓋と等しい)なので、順番に計算してゆきます。
2.1 上蓋と底蓋の体積を与える計算式
上蓋と底蓋は下図のハッチング部分で、同体積です。

この部分の体積は、下図のように、薄い円板を積み重ねたものです。

それぞれの薄板の体積dV1は次式の通りで、

それらを足し合わせて、各板厚を限りなく薄くしたものが、上蓋、底蓋の体積V1です。

2.2 胴部の体積を与える計算式
胴部の体積は、上蓋と同じように、下図に示す薄い円板を積み重ねたものなので、

それぞれの薄板の体積dV2は次式の通りで、

これらを足し合わせたものが、胴部の体積V2です(この式は上半分のみ)
2.3 空隙の体積を与える計算式
容器の体積Vは次式の通りで、

中球と小球の体積Vrは、

なので、空隙の体積Vvoidは次式の通りとなります。

2.4 黄色の円と緑の円の交点を与える計算式
具体的に計算していくためには、黄色と緑の交点Bの座標を求めておく必要があります。

上図に示した交点Bのx座標は、

y座標は、

θ0は、ベクトルOAとベクトルOBが得られたので余弦定理から、

同様にして、φ0が次式から求まります。

2.5 ようやく、空隙の体積にたどり着く
上述の計算式に、r1=1寸、r2=1.5寸を代入すると、r3=4寸、r4=5寸。黄色と緑の円の交点座標は(2.25, 3.3072)、θ0=34.2289°、φ0=41.4096°が得られます。
容器の体積はV=54.4644立方寸、3つ球体の体積の和はVr=32.4631立方寸で、空隙の体積としてVvoid=22.0013立方寸が求まります。
算額には答えとして「二十二歩有奇」と記載されているので、両者の数値は合致しているといえます。またしても、単位が「歩」と書かれていますが、これは「立方寸」のはず。
3.おわりに
今回も「腕力」で解きましたが、江戸時代の数学では、どんな風に解いて、どれほどの時間を要したことか。
それにしても、なぜ、「平方寸」であろうが「立方寸」であろうが、算額では単位を「歩」と記するのでしょうね。金箔や着物の生地など高価な素材の面積に限っては「平方寸」を「歩」と呼ぶこともあったようです(←景気付け?)が、体積について「歩」を用いるような慣習は見当たらず、基本単位は「升」、10分の1が「合」、10倍が「斗」です。落語「居酒屋」では、客が酒一合を注文すると、小僧さんが「燗 一升〜!」とオーダーを入れて景気づける場面があったりしますが。
ちなみに、祝いごとで2本の一升瓶の酒(=2升)に「一斗二升五合」(=12.5升)と書いた札を下げて贈り物にする慣習があります。これは、「五升の2倍、一升と一升、一升の半分」→「ご商売、益々、繁盛」と読ませるものです。
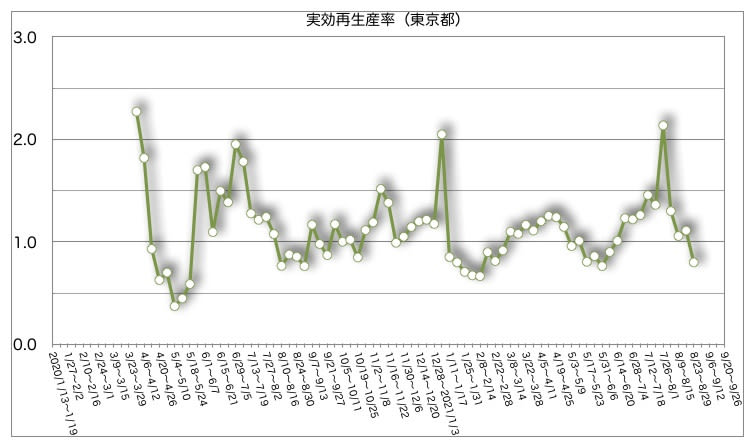
今日29日、日曜日までの累積人数のグラフです(1週間前のグラフを更新しました)。

減少に転じましたが、報道によると盆休みの影響だと説明されています。

実効再生産率が0.80倍に低下しています。これまでの傾向からすると、増加するときは1.2倍、減少するときは0.8倍なわけですが、これほどピッタリなのは単なる偶然なのでしょうか。デルタ株の出現により感染率が上昇しているのだから、それ以上に人出が減っていないと辻褄が合わない話なのですが・・・
【人数の出典】
東京都の人数:東京都新型コロナウイルス感染症対策サイト(チャーター機帰国者、クルーズ船乗客等を含まず
今日も、クロアゲハが一羽、ひらひらと翔び立ってゆきました
肩は注射で劇的に改善したものの、まだまだ限界があります。
夜、寝ようと横たわると、まだ痛むし
ごはんは、作るときより、食べるときの方が腕をあげる動作が加わるので一苦労
生姜には消炎作用があるので、舞茸そぼろを生姜たっぷりで作ってみました
舞茸を細かく刻んで、

生姜をたっぷり刻んで、

合挽きは、ほぐさずに焼き目をつけて、

舞茸、生姜、酒、みりん、砂糖、醤油を加え、菜箸でほぐして、

煮詰めたら、できあがり。

舞茸そぼろ丼にしたり、

舞茸そぼろうどんにして

今日、実家に行くためにバス停で時刻表を確認していたら、ちょうどバスが接近
ラッキー とばかり乗車して約10分、忘れ物に気づいて降車ボタンをピンポン
とばかり乗車して約10分、忘れ物に気づいて降車ボタンをピンポン
すっかり、戦意喪失 
ミキプルーンは、よく耳にしますが、涼麻父にとって生プルーンは初。

紅茶コンポートにしてみました
まず、アボカドのように半割りにして、種を外して、4つにカットして、

濃いめに淹れたダージリン100mL

三温糖大さじ1、

弱火で、ことこと20分

レモン汁を加えると煮汁が真っ赤に染まります。これはプルーンに含まれるアントシアニンのなせる業です。

粗熱をとって、

冷蔵庫で冷やします

煮汁が少なすぎたようです
肩は、横と後ろには動くようになりましたが、前や上にはまだイマイチ

ゆず坊たちが、次々と蛹化して、どこかへ引っ越してゆきますが、この子は植木鉢の表側をチョイス。
なかなか大胆な子です

ある朝、様子を見るためにベランダに出たら、視界の隅になにやら黒いものが
あれま、こんなに目立つところにも蛹がいたっけ?
ちょうど、もぞもぞと蛹から出てきたところでした。

しばらくすると、羽を拡げ始めました。まだ、しっとりとしています。

で、この後、涼麻父はお医者さんに行って、帰りに調剤薬局に寄って、お昼前に帰ってきたんですが、もう羽化した場所にはおらず、1〜2m離れたベランダの片隅で羽を乾かしていて、涼麻父の姿を見ると、植栽の方へと翔んでゆきました。羽が乾き切っていないときは、涼麻父が近づいても逃げることはないので、ちょうど乾いてきて、そろそろというタイミングだったのでしょう。
この子は、クロアゲハ♀でした

こういうとき、アゲハは2〜3回、ベランダの方へ戻ってきて挨拶をしてから、南の方へ翔び立ってゆきます
実際のところ、羽化したばかりのアゲハは、まだ翔ぶことに慣れていないので、もとの安全な場所に戻れる範囲で旋回しているのだと思いますが、涼麻父は、これを「律儀」と呼んでいます
庚申塔を巡って歩いていると、ときどき梵字の列に出会います。
密蔵院の前庭に立つ馬頭観世音板碑の上部に描かれていた梵字。
中央は、馬頭観音の種字「カン」
それを取り囲む11文字の梵字は、馬頭観音の真言で「オン・アミリト・ドバンバ・ウン・ハッタ・ソワカ」でした。

一番下の文字から時計回りに読んでゆくようです。
「三宿二丁目の庚申塔」の堂宇の横に立っていた三界萬霊塔の上部の梵字。
中央の5文字は、五大(地水火風空)を表す「ア・ビ・ラ・ウン・ケン」。中央、下、左、上、右の順に読むようです。
五輪塔の空風火水地では「キャ・カ・ラ・バ・ア」と記するのとは異なっていますね。

周囲を巡る24文字は光明真言といい、金剛界五仏に光明を放つようにお願いする真言でした。やはり、一番下の文字から時計回りに読んで、「オン ア ボ キャ ベイ ロ シャ ノウ マ カ ボ ダラ マ ニ ハン ドマ ジンバ ラ ハラ バ リタ ヤ ウン」
金剛界五仏は五智如来とも呼ばれ、大日如来(中央)、阿閦如来(東方)、宝生如来(南方)、阿弥陀如来(西方)、不空成就如来(北方)のことです。東寺講堂の立体曼荼羅のうち、中央の5体が五智如来です。
この石塔のように、中央に五大、周囲に光明真言を配した形式を「光明曼荼羅」と呼ぶのだそうです
涼麻父、人生初の三角巾です 

涼麻父、五十肩の急性期だと思い込んでいたのですが、 肩の可動範囲がほぼゼロであること、
肩の可動範囲がほぼゼロであること、 激痛であることなどから、整外の先生の見立ては別の病名でした。
激痛であることなどから、整外の先生の見立ては別の病名でした。
でも、先生にとっては珍しいことでも何でもなく、即座に、X線で確認、関節注射で対処、痛み止めでフォローと相成りました。
効果てきめんで、夜、痛みのために一睡もできなかったことが、まるで嘘のようです。
餅は餅屋、やっぱり、優秀な専門家は ありがたいものです
久しぶりにひじきを食べようか
乾物って便利ですね
野菜天ぷら(さつま揚げ)を買ってきて、

ひじきを20分ほど水で戻して、

油で炒めて、

水100mLを加え、短冊に切ったさつま揚げと、醤油大さじ1、みりん大さじ1、砂糖大さじ1。

通例では出汁を使いますが、さつま揚げから出汁が出るから水でも 
このことは、土井善晴から学びました。
煮詰めたらできあがり

涼麻父、五十肩?を悪化させてしまいました。
軽く痛むくらいだったのですが、動かなくなったらいけないと思い、肩を回していたら、これが典型的な逆効果
炎症なのだから、安静に動かさないようにしていた方が良いようです
利き手の方なので、不便なこと、この上ありません
神楽坂の毘沙門天さま。20年ぶりくらいだったかも
文禄4年(1595)に馬喰町で開創、その後、火事で焼失し、寛文10年(1670)に麹町に移転、寛政4年(1792)年の火事で神楽坂に引っ越してきたという経緯があります。

本尊の毘沙門天は御簾の向こうなので、御前立ちを拝みます。ご開帳は年に3回(正月、5月、9月の寅の日)のみで、次回は9月3日だそうです。
狛犬が虎です。これは、毘沙門天が寅年、寅の月、寅の日に初めてこの世に姿を現したという話に因んだものです。

ちゃんと阿吽のペアです。

安山岩に、うまい具合に虎柄が表現されています。

基台に「横棒と上矢印」を組み合わせた印が刻まれていますが、これは、几号水準点と呼ばれる測量上の目印で、明治初期にお雇い英国人の指導で、道標や灯篭などに付されたようです。

石像などは「動かない」とみなしていたということですね。でも、日本は火山や地震のために地面自体が隆起したり沈降しちゃいますから、GPSのなかった時代は苦労したに違いありません。
ゴーヤーといったら、ちゃんぷるー

スパムを短冊に切って、焼き目を入れて、

ゴーヤーの薄切りに軽く塩をふって、炒めて、

水切りしておいた豆腐をちぎり入れて、

溶き卵をからめ、鍋肌からしょうゆをひと回し、

あっという間に できあがり〜

今日22日、日曜日までの累積人数のグラフです(1週間前のグラフを更新しました)。

やはり先週の鈍化は3連休の影響で、一時的なものだったようです。

実効再生産率が1.11倍に増加、依然として1以上なので医療逼迫度を悪化させてゆく可能性が高いといえます。

【人数の出典】
東京都の人数:東京都新型コロナウイルス感染症対策サイト(チャーター機帰国者、クルーズ船乗客等を含まず
伊佐爾波神社に奉納された算額から、佐野長次郎の算額(天保三年、1832年)を解いてみました。
絵馬の写真の転載が禁止されていますので、説明図を描き起こしました。仮に写真を転載できたとしても、オリジナルの絵馬は色褪せてしまって判読が困難な状態なので、「道後八幡 伊佐爾波神社の算額, 伊佐爾波神社, 2005」を参照しました。

問題を要約すると次のようになります。
何枚かの正方形がある。2番目の正方形は、辺の長さが、1番目の正方形の辺の長さより2/5だけ短い。3番目の辺の長さは2番目の辺の長さより2/5だけ短く、以下同様に、小さなってゆく正方形がある。
すべての正方形の辺の長さを足し合わせると966,721寸で、すべての正方形の面積を足し合わせると338,394,365,321歩だったという。このとき、1番目の正方形の辺の長さはいくつか。
0.はじめに
まず、この設問には2箇所の誤記があります。正方形の面積は「338,394,365,321歩」ではなく、正しくは「238,394,365,321平方寸」です。数字の誤記は、おそらく手元のメモを絵馬に清書するために代書してもらった際に生じたものと思われます。また、単位の方は作者の錯誤によるものではないかと推測します。このあたりについては、第2章に整理して示します。
1.解いてみる
1.1 方程式を導いて計算式を得る
1番目の正方形の辺の長さをxとします。そうすると、2番目の辺の長さは3/5 x、3番目は9/25 x・・・となります。正方形の枚数をn枚とすると、正方形の辺の長さの総和Lは、
 ...... (1)
...... (1)
で、正方形の面積の総和Sは、
 ...... (2)
...... (2)
となります。
式(1)の両辺に3/5をかけて、
 ...... (3)
...... (3)
式(1)と式(3)の差をとると、
 ...... (4)
...... (4)
となるので、次の通り、Lとn及びxの関係が得られます。
 ...... (5)
...... (5)
次に、式(2)の両辺に(3/5)2をかけて、
 ......(6)
......(6)
式(2)と式(6)の差をとると、
 ......(7)
......(7)
となり、Sとn及びxの関係が得られます。
 ......(8)
......(8)
式(5)と式(8)からnを消去しようと思います。式(5)を変形して、
 ......(9)
......(9)
この式(9)を式(8)に代入すれば、
 ......(10)
......(10)
これを整理すれば、xとL及びSの関係式が得られます。
 ......(11)
......(11)
1.2 答えを計算する
式(11)に、L=966,721寸、S=238,394,365,321平方寸を代入すれば、

が得られます。この値は、絵馬に記されている解答「三十九万零六百二十五寸」と一致しています。
絵馬には、この値を得るための計算式として「置積和以方面和除之名極以減方面和餘乗分子以分母及二除之加極」と示されています。これを書き下すと、「道後八幡 伊佐爾波神社の算額」によれば、

となり、式(11)が絵馬の計算式と一致していることが確認できました。
1.3 正方形の総枚数nはどうなっているのか
正方形の枚数nを求めるには、式(9)のxに式(11)を代入して、
 ......(12)
......(12)
式(12)で両辺のlogをとれば、
 ......(13)
......(13)
となり、式(14)が得られるので、
 ......(14)
......(14)
式(14)のL及びSに数値を代入すれば、

n=9枚であったことがわかります。
2.本当に誤記なのか
2.1 「歩」とは
「歩」は尺貫法で面積を表す単位で、1歩=1間×1間です。1間=6尺、1尺=10寸なので、1歩=60寸×60寸=3,600平方寸です。
ちなみに、現代のメートル法によれば、1寸=30.303mm、1尺=303.03mm、1間=1.8182m、1歩(=1坪)=3.3058m2なので、やはり1步=3,600平方寸となります。
絵馬には、S=338,394,365,321歩と記されているので、その通りだとすると、S=338,394,365,321歩÷3,600=93,998,434.81平方寸です。この値を、絵馬の計算式にも記載されている式(11)に代入してxを求めると966,726寸となり、これは絵馬自身に示されている解答390,625寸と一致しません。さらに、式(14)を用いてnを求めようとしてもlogの中身が負となるので計算できません。つまり、このような条件設定はあり得ないということになります。
もし、S=238,394,365,321歩だったとしても、S=66,220,657.03平方寸で、x=193,399寸となり、これもまた絵馬の解答と一致せず、やはりnが求まりません。
これらのことから、「歩」と「平方寸」の錯誤があったと考えるのが妥当でしょう(あるいは、Lを表す単位が「間」であるべきところ、「寸」と錯誤したのかも知れませんが、状況は同じです)。
2.2 面積和Sについて
正方形の枚数が増えるほど、辺や面積の総和も増えてゆきますが、実は無際限に増えるのではなく上限値があります。
正方形の枚数がn=1のとき、辺の総和はL1=xで、面積の総和はS1=x2です。n枚のときは、式(5)と式(8)に示した通りで、
 ...... (5)
...... (5)
 ......(8)
......(8)
(3/5)=0.6<1なので、n→∞とすると(3/5)n→0、(3/5)2n→0となり、L<5/2、S<25/16です。すなわち、
 ...... (15)
...... (15)
 ...... (16)
...... (16)
となります。具体的に、絵馬に示されている値x=390,625寸を式(15)、式(16)に代入すると、
 ......(17)
......(17)
 ...... (18)
...... (18)
となります。絵馬には L=966,721、S=338,394,365,321と記されていて、Lは式(17)の範囲に含まれていますが、一方、Sは式(18)の範囲を逸脱しており、すなわち、Sがあり得ない設定になってしまっていることがわかります。
そこで、x=390,625寸、L=966,721寸を式(11)に代入してみると、S=238,394,365,321平方寸となるので、やはり誤記だったのだと考えられます。
3.問題の作り方について考えてみる
3.1 腕力への挑戦状なのか
この問題は、はじめに正方形の枚数nと1番目の正方形の辺の長さxを決めれば、式(5)と式(8)を用いて、SとLを決めることができます。その意味で、この問題は、作者が答えを知っているのです。一方、例えば、先日、解いてみた金王八幡の設問の場合は、作者も答えがどんなことになるかを事前には知らず、自分自身で解いてみているのです。いわば、作者が「これって、どうやって計算するんだろう?」と思い、取り組んだ結果を算額にしたためているのです。その意味で、今回の設問は趣を異にします。
この問題では、面積和Sとして桁違いに大きな数字を設定しています。実は、問題の解き方を問うだけならば、n=9枚、x=100寸として、L=247.48寸、S=15,623.41平方寸くらいの桁数でも、十分、成り立つのです。実際に、これらのL、Sの値を式(11)に代入すればx=100寸が得られます。それにも関わらず、設問ではSとして12桁もの巨大な数字を設定しています。当時の計算は算木を使い、忍耐強く正確な作業を続けることが求められるので、「腕力」に対する挑戦状のようにも思えてしまいます。あるいは、答えの390,625が、なにかの語呂合わせになっていて、それを表すためには、どうしても桁数を増やす必要があった、などという話であれば、それはまた面白そうなのですが、実は、この設定には理由があったのです(3.3節で説明します)。
3.2 枚数の話はどうするつもりだったのか
問題を作る際には、正方形の枚数nを好きなように決めてかけ算を繰り返せば良いのですが、解く際にはlogを使わなければならないので大変です。現代では式(14)を用いて、電卓で一発なのですが、当時はどうだったのでしょう。マクローリン級数を使うとなると、

が一般的ですが、この式は収束が遅い(なかなか精度の良い値が得られない)ため、実務的には、次の式が用いられます。

しかし、この式とて、第20〜30項くらいまで足し合わせてゆく必要があり、その計算量が超膨大になることは想像に難くありません。なお、設問では、特段、枚数nについては問うていませんし、nを与える計算式にも触れていません。
3.3 明示されていないヒント
3.1節では、試しにL=247.48寸、S=15,623.41平方寸という設定をしてみましたが、これは小数点を含む半端な数字です。しかし、設問の数字の末尾には「有奇」という表記がないので、ぴったりの数字(小数点以下がない自然数)だ、ということを暗示的に示している可能性が考えられます。
仮にxやL、Sなどが小数点以下を含む場合でも、第1章に示した方法で解くことは可能です(2つの未知数n、xに対して2つの条件L、Sがあるので)。しかし、もしも、この問題が自然数(正である整数=1、2、3、……)に限定される話ならば、これは現代数学でいうところの「整数論」であって、別の解き方が可能になります。つまり、この問題では、明示的に示されている2つの条件に加えて、x、L、Sが自然数である、という条件(ヒント)が暗示されているのです(nは枚数なので、当然に自然数です)。
3.4 整数論で解いてみる
1番目の正方形の面積の辺の長さxは、順次3/5倍になってゆきます。このとき、各正方形の辺の長さが半端にならず自然数になるならば、それは、毎回5で割り切れる、ということです。n枚の正方形が登場するならば、5で(n-1)回、割っても割り切れるというのがxの特性です。
すなわち、xは次式で表されます。
 (m:任意の自然数)......(19)
(m:任意の自然数)......(19)
そうすると、2枚目の正方形の辺の長さは、xの3/5倍なので、
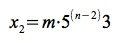
同様にして、3枚目は、

最後(n枚目)の正方形は、

となります。ちなみに、最後の正方形の辺の長さは、xに3を(n-1)回かけて出てきた数字なので、3で(n-1)回、割っても割り切れるようにできています。
さて、Lは、これらの辺の長さの総和ですから、
 ...... (20)
...... (20)
と表すことができます。
さて、L=966,721でした。この数字を、法5(mod 5)のもとで展開してみます。
966,721÷5=193,344 余り1
193,344÷5=38,668 余り4
38,668÷5=7,733 余り3
7,733÷5=1,546 余り3
1,546÷5=309 余り1
309÷5=61 余り4
61÷5=12 余り1
12÷5=2 余り2
となるので、

と表すことができます。この式を次のように変形していきます。

となります。この最後の式を、式(20)と見比べると、式(20)でm=1、n=9としたときと一致することがわかります。すなわち、正方形の枚数はn=9枚です。
また、1番目の正方形の辺の長さxは、式(19)から、

であることがわかります。これらの値は、もちろん、第1章で求めた答えや絵馬に記された解答と一致しています。
すなわち、答えであるx=390,625は、デタラメでもないし、語呂合わせでもないし、無用に桁数を多くしているわけでもなく「5の8乗」という、意味のある数字だったのです。
第3章に示した解き方は、第1章の猛烈に腕力が必要な解き方と比べると、はるかに計算量が少なく、またスマートです。さらに、S=238,394,365,321という条件を使わずとも答えが得られるのです(もちろん、Sの条件のみを使ってLの条件を使わない方法でも同じ答えにたどり着きます)。これは、「x、L、Sが自然数である」という条件を活用したからです。
作者が企図したのは、こういった捉え方でもあったのではないかと想像されます。
4.おわりに
整数論は、暗号作成や復元に使われるほか、チェックデジットの考え方にも活用されています。扱う数値を、無数に存在し得る実数に代わり整数に制限することで、半端な答えが登場しなくなるので、暗号の復号やチェックデジットを確認する上で便利です。
さらに、扱う数値が整数だけなので、その条件を活用することで整数論ならではの解き方が可能になります。それを考慮した上で、本題を「正方形の辺の総和のみを与えて、はじめの正方形の辺の長さ、正方形の枚数、正方形の面積の総和を求めよ」というように、未知数より条件式が少なくて、一見すると解けないのではないか、と思わせる設問に改作してもおもしろいかも知れません。
「蛸薬師」から南下、林試の森公園をかすめて、かむろ坂通りを西進。15分ちょっとで「お猿橋庚申塔」。
この変形四叉路の東側にあります。写真の右奥から左手前への道が、もとは品川用水(碑文谷みち)で、このあたりに「お猿橋」があったそうです。

この頃、雨がポツリポツリと降り始め、早足になっていたら、うっかり通り過ぎてしまいました

内部はコンクリートブロックですが、ファサードの柱と梁は伝統建築です。

三猿文字塔。文字は摩滅していて判読できないが、説明板によれば「汝等所行是菩薩道漸々修学子孫悉當成仏」で、延宝二年(1674年)建立とのことです。
三猿は、言わざる、聞かざる、見ざる。

このあたりで傘が必要なほどの雨降りになってきました。武蔵小山駅まで10分ほど

この日のストロールは、ここまで 
やっぱり、夏はカレー
にんじん、じゃがいもを茹でて、

カルダモン、クローブ、コリアンダーを油で熱して、

いつものように作りましたが、仕上げは、ナンプラー大さじ1、インスタントコーヒー大さじ1に、今回は、爽やかさを求めて自家製チャツネを多めに大さじ2。

食べるときに、さらにチャツネを加えると良いです 

















 『舞妓さんちのまかないさん』NHK Eテレ, 土曜日, 9:20~9:29
『舞妓さんちのまかないさん』NHK Eテレ, 土曜日, 9:20~9:29





