神戸市教員採用試験小学全科2

次の図で直線lはy＝xのグラフで点Ａ、Ｂの座標はそれぞれ（4,2)、(18,12)である。直線l上に点PをとってＡP＋PＢを最小にしたい。直線lについて点Ａと対称な点Ｃを考えることによりＡP＋PＢの最小の値を求めよ。

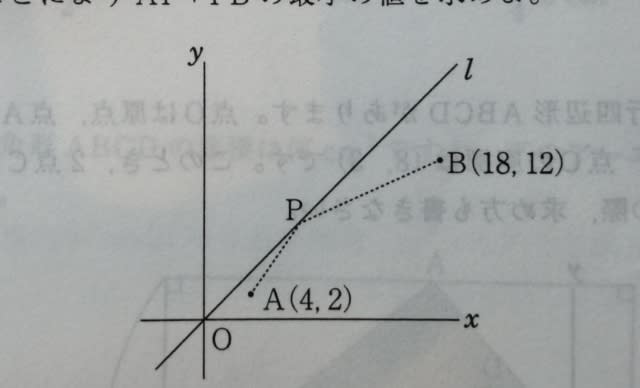
(1) 直線lについて点Ａと対称な点Ｃを求め、点Ｃの座標(ア,イ)に当てはまる数を、それぞれ1〜0から選び、番号で答えよ。



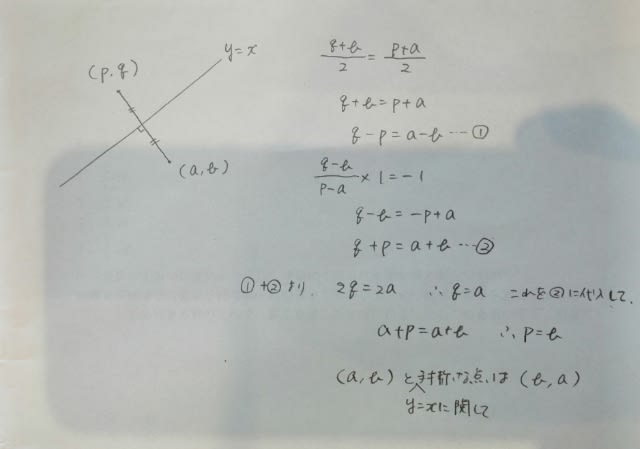
(1)　こうするのが一般的です。

ただし、本問に限っては、たまたまy＝xに関して対称な点なので、Ａ（４,2)の、x座標とy座標を入れかえた(2,4)がＣの座標となります。
簡単に証明しておきます。

(2)　Ａからl上の点にタッチしてＢに行くとき、これが一番早いでしょうか?

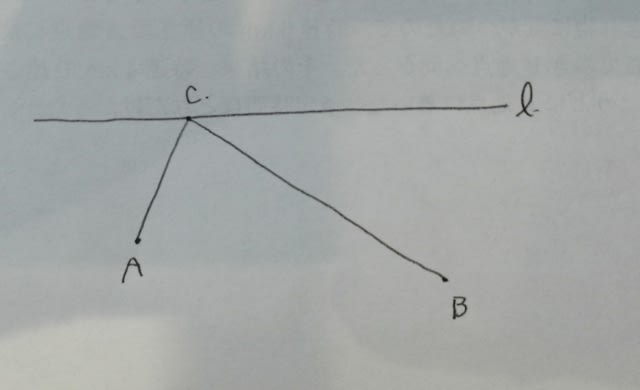
そんなことはありません。なぜなら、


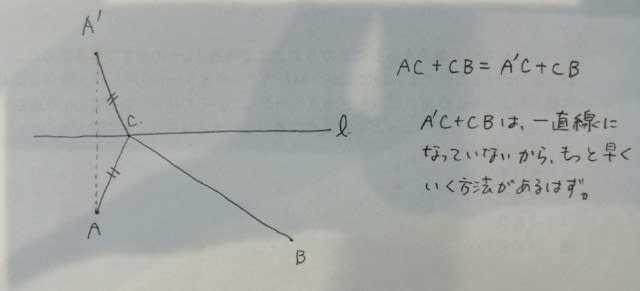
一番早く行きたければ、ÁとＢを結んだ線分とlとの交点目指して進むのがベストですね。


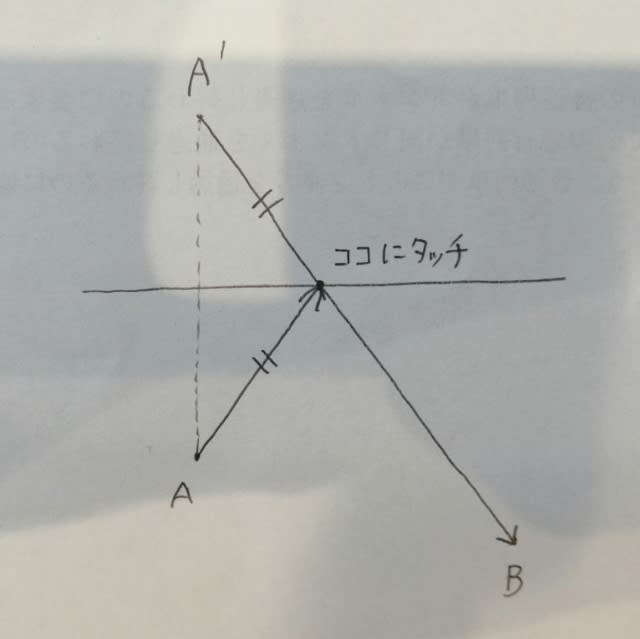
よって、本問の場合は、こうなります。


正解は、３です。ＣＢの長さは、次のようにしても構いませんよ。

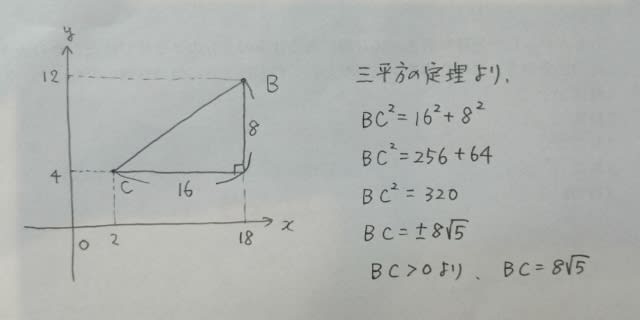
まあ、どちらも同じことをしているのですが。ここをポチッとお願いします。→
にほんブログ村