図のような八つの部屋があるホテルに、A~Fの6人が一つの部屋につき1人ずつ宿泊しており、二つの部屋は空室である。次のことが分かっているとき、確実にいえるのはどれか。 ○Aの部屋の隣には、空室が少なくとも一つある。また、Bの部屋の隣にも、空室が少なくとも一つある。 ○Aの部屋と廊下を挟んで真向かいにある部屋の隣は、Dの部屋である。 ○Bの部屋と廊下を挟んで真向かいにある部屋は、Eの部屋である。 ○Dの部屋と廊下を挟んで真向かいにある部屋は、空室である。 ○Cの部屋とEの部屋は、それぞれ5号室と7号室又は7号室と5号室である。 ①1号室はBの部屋である。 ②2号室は空室である。 ③3号室はAの部屋である。 ④6号室はDの部屋である。 ⑤8号室は空室である。 最後の条件より、次の2つしかありません。
○Aの部屋の隣には、空室が少なくとも一つある。また、Bの部屋の隣にも、空室が少なくとも一つある。 ○Aの部屋と廊下を挟んで真向かいにある部屋の隣は、Dの部屋である。 ○Bの部屋と廊下を挟んで真向かいにある部屋は、Eの部屋である。 ○Dの部屋と廊下を挟んで真向かいにある部屋は、空室である。 ○Cの部屋とEの部屋は、それぞれ5号室と7号室又は7号室と5号室である。 ①1号室はBの部屋である。 ②2号室は空室である。 ③3号室はAの部屋である。 ④6号室はDの部屋である。 ⑤8号室は空室である。 最後の条件より、次の2つしかありません。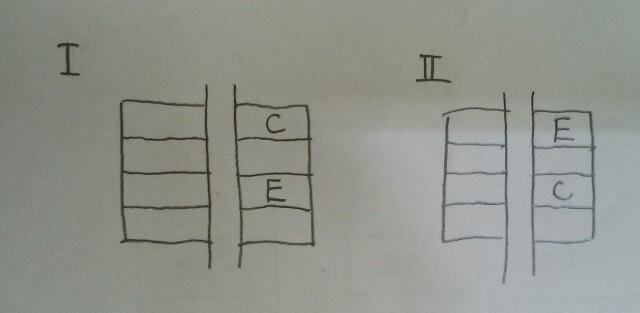 3つめの条件より、EとBは、向かい合っていますから、
3つめの条件より、EとBは、向かい合っていますから、 2つめの条件。Aの向かいの隣がDです。 「向かいの隣」も、「隣の向かい」も、全く同じで、要するに「斜め」ですね。 図Ⅰを見ると、AとDは、1号室と6号室に入るしかありません。ただ、1番目の条件より、Aの隣には空室が必要なので、Aが1号室でDが6号室で2号室は空室ですね。(4つめの条件、「Dの真向かいが空室」も自動的に満たしている)
2つめの条件。Aの向かいの隣がDです。 「向かいの隣」も、「隣の向かい」も、全く同じで、要するに「斜め」ですね。 図Ⅰを見ると、AとDは、1号室と6号室に入るしかありません。ただ、1番目の条件より、Aの隣には空室が必要なので、Aが1号室でDが6号室で2号室は空室ですね。(4つめの条件、「Dの真向かいが空室」も自動的に満たしている) Fと、もう一つの空室は、4号室と8号室で、入れ替え可。
Fと、もう一つの空室は、4号室と8号室で、入れ替え可。 図Ⅱの場合は、AとDは、3号室と6号室又は3号室と8号室に入ります。Aの隣は空室なので、どっちにしてもAは3号室です。もしもDが6号室ならば………。
図Ⅱの場合は、AとDは、3号室と6号室又は3号室と8号室に入ります。Aの隣は空室なので、どっちにしてもAは3号室です。もしもDが6号室ならば………。 Bの隣は空室なので、2号室は空室で、(これで1番目の条件も4番目の条件もクリアー)Fと、もう一つの空室は4号室と8号室で、入れ替え可。
Bの隣は空室なので、2号室は空室で、(これで1番目の条件も4番目の条件もクリアー)Fと、もう一つの空室は4号室と8号室で、入れ替え可。 もしもDが8号室ならば………。
もしもDが8号室ならば………。 4番目の条件(Dの真向かいは空室)より、4号室は空室で、1番目の条件(Bの隣には空室がある)より、2号室も空室。残ったFは6号室。
4番目の条件(Dの真向かいは空室)より、4号室は空室で、1番目の条件(Bの隣には空室がある)より、2号室も空室。残ったFは6号室。 結局、3種類(Fと空室の入れ替えを考慮すると5通り)考えられます。
結局、3種類(Fと空室の入れ替えを考慮すると5通り)考えられます。 ①1号室はAということもあり得る。②正解。③3号室はBということもあり得る。④6号室はFということもあり得る。⑤8号室は、FやDということもあり得る。ここをポチッとお願いします。→
①1号室はAということもあり得る。②正解。③3号室はBということもあり得る。④6号室はFということもあり得る。⑤8号室は、FやDということもあり得る。ここをポチッとお願いします。→
にほんブログ村

 ○Aの部屋の隣には、空室が少なくとも一つある。また、Bの部屋の隣にも、空室が少なくとも一つある。 ○Aの部屋と廊下を挟んで真向かいにある部屋の隣は、Dの部屋である。 ○Bの部屋と廊下を挟んで真向かいにある部屋は、Eの部屋である。 ○Dの部屋と廊下を挟んで真向かいにある部屋は、空室である。 ○Cの部屋とEの部屋は、それぞれ5号室と7号室又は7号室と5号室である。 ①1号室はBの部屋である。 ②2号室は空室である。 ③3号室はAの部屋である。 ④6号室はDの部屋である。 ⑤8号室は空室である。 最後の条件より、次の2つしかありません。
○Aの部屋の隣には、空室が少なくとも一つある。また、Bの部屋の隣にも、空室が少なくとも一つある。 ○Aの部屋と廊下を挟んで真向かいにある部屋の隣は、Dの部屋である。 ○Bの部屋と廊下を挟んで真向かいにある部屋は、Eの部屋である。 ○Dの部屋と廊下を挟んで真向かいにある部屋は、空室である。 ○Cの部屋とEの部屋は、それぞれ5号室と7号室又は7号室と5号室である。 ①1号室はBの部屋である。 ②2号室は空室である。 ③3号室はAの部屋である。 ④6号室はDの部屋である。 ⑤8号室は空室である。 最後の条件より、次の2つしかありません。 3つめの条件より、EとBは、向かい合っていますから、
3つめの条件より、EとBは、向かい合っていますから、 2つめの条件。Aの向かいの隣がDです。 「向かいの隣」も、「隣の向かい」も、全く同じで、要するに「斜め」ですね。 図Ⅰを見ると、AとDは、1号室と6号室に入るしかありません。ただ、1番目の条件より、Aの隣には空室が必要なので、Aが1号室でDが6号室で2号室は空室ですね。(4つめの条件、「Dの真向かいが空室」も自動的に満たしている)
2つめの条件。Aの向かいの隣がDです。 「向かいの隣」も、「隣の向かい」も、全く同じで、要するに「斜め」ですね。 図Ⅰを見ると、AとDは、1号室と6号室に入るしかありません。ただ、1番目の条件より、Aの隣には空室が必要なので、Aが1号室でDが6号室で2号室は空室ですね。(4つめの条件、「Dの真向かいが空室」も自動的に満たしている) Fと、もう一つの空室は、4号室と8号室で、入れ替え可。
Fと、もう一つの空室は、4号室と8号室で、入れ替え可。 図Ⅱの場合は、AとDは、3号室と6号室又は3号室と8号室に入ります。Aの隣は空室なので、どっちにしてもAは3号室です。もしもDが6号室ならば………。
図Ⅱの場合は、AとDは、3号室と6号室又は3号室と8号室に入ります。Aの隣は空室なので、どっちにしてもAは3号室です。もしもDが6号室ならば………。 Bの隣は空室なので、2号室は空室で、(これで1番目の条件も4番目の条件もクリアー)Fと、もう一つの空室は4号室と8号室で、入れ替え可。
Bの隣は空室なので、2号室は空室で、(これで1番目の条件も4番目の条件もクリアー)Fと、もう一つの空室は4号室と8号室で、入れ替え可。 もしもDが8号室ならば………。
もしもDが8号室ならば………。 4番目の条件(Dの真向かいは空室)より、4号室は空室で、1番目の条件(Bの隣には空室がある)より、2号室も空室。残ったFは6号室。
4番目の条件(Dの真向かいは空室)より、4号室は空室で、1番目の条件(Bの隣には空室がある)より、2号室も空室。残ったFは6号室。 結局、3種類(Fと空室の入れ替えを考慮すると5通り)考えられます。
結局、3種類(Fと空室の入れ替えを考慮すると5通り)考えられます。 ①1号室はAということもあり得る。②正解。③3号室はBということもあり得る。④6号室はFということもあり得る。⑤8号室は、FやDということもあり得る。ここをポチッとお願いします。→
①1号室はAということもあり得る。②正解。③3号室はBということもあり得る。④6号室はFということもあり得る。⑤8号室は、FやDということもあり得る。ここをポチッとお願いします。→にほんブログ村






















※コメント投稿者のブログIDはブログ作成者のみに通知されます