二つの円が接していて、そこに共通接線が引いてあったとします。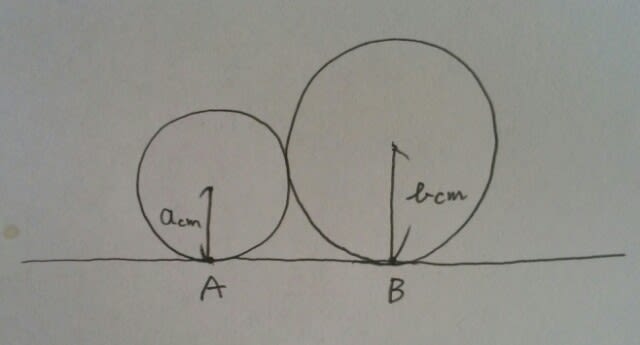 さて、線分ABの長さはいくらになるでしょうか?以前、図形の3つの手筋を紹介しましたが、円と接線があれば、円の中心と接点を結ぶ(すると90°になる)。円や球が外接していれば、中心どうしを結ぶのでした。
さて、線分ABの長さはいくらになるでしょうか?以前、図形の3つの手筋を紹介しましたが、円と接線があれば、円の中心と接点を結ぶ(すると90°になる)。円や球が外接していれば、中心どうしを結ぶのでした。 O1からO2Bに垂線をおろして、その交点をCとします。
O1からO2Bに垂線をおろして、その交点をCとします。 四角形O1ABCは、3つの角が90°なので、もう一つの角も90°になり、長方形です。長方形は、向かい合う辺の長さが等しいので、AB=O1Cです。
四角形O1ABCは、3つの角が90°なので、もう一つの角も90°になり、長方形です。長方形は、向かい合う辺の長さが等しいので、AB=O1Cです。 O2C=O2B-CB=b-a。△O2O1Cは、直角三角形なので、三平方の定理より、
O2C=O2B-CB=b-a。△O2O1Cは、直角三角形なので、三平方の定理より、 こ~んなにきれいにまとまっちゃうので、これは公式として覚えておけば、とても役にたちますよ。 例えば、平成29年国家一般職(大卒)より。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。
こ~んなにきれいにまとまっちゃうので、これは公式として覚えておけば、とても役にたちますよ。 例えば、平成29年国家一般職(大卒)より。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。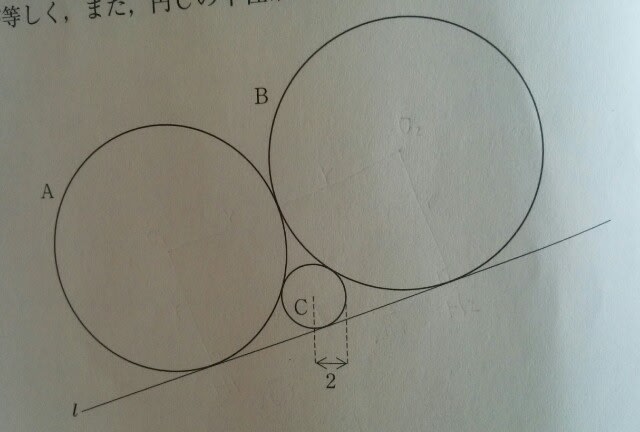 ①4√3②7③8④6√2⑤9 円Aと円Bの半径をrとすると、
①4√3②7③8④6√2⑤9 円Aと円Bの半径をrとすると、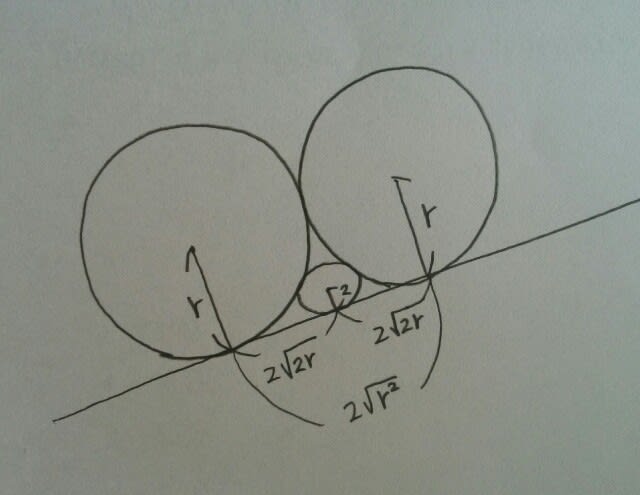 よって、
よって、 正解は、肢③です。 もういっちょう~。平成22年地方上級より。次の図のように、半径3cmの円と半径6cmの円が点Cで接している。2つの円に接する3本の接線の交点をO、A、Bとするとき、ABの長さはどれか。
正解は、肢③です。 もういっちょう~。平成22年地方上級より。次の図のように、半径3cmの円と半径6cmの円が点Cで接している。2つの円に接する3本の接線の交点をO、A、Bとするとき、ABの長さはどれか。 ①3√6cm②6√2cm③9cm④4√6cm⑤6√3cm 円外の1点から引いた2つの接線の長さは等しいので、
①3√6cm②6√2cm③9cm④4√6cm⑤6√3cm 円外の1点から引いた2つの接線の長さは等しいので、 ってな具合で、正解は、肢②です。ここをポチッとお願いします。→
ってな具合で、正解は、肢②です。ここをポチッとお願いします。→
にほんブログ村

 さて、線分ABの長さはいくらになるでしょうか?以前、図形の3つの手筋を紹介しましたが、円と接線があれば、円の中心と接点を結ぶ(すると90°になる)。円や球が外接していれば、中心どうしを結ぶのでした。
さて、線分ABの長さはいくらになるでしょうか?以前、図形の3つの手筋を紹介しましたが、円と接線があれば、円の中心と接点を結ぶ(すると90°になる)。円や球が外接していれば、中心どうしを結ぶのでした。 O1からO2Bに垂線をおろして、その交点をCとします。
O1からO2Bに垂線をおろして、その交点をCとします。 四角形O1ABCは、3つの角が90°なので、もう一つの角も90°になり、長方形です。長方形は、向かい合う辺の長さが等しいので、AB=O1Cです。
四角形O1ABCは、3つの角が90°なので、もう一つの角も90°になり、長方形です。長方形は、向かい合う辺の長さが等しいので、AB=O1Cです。 O2C=O2B-CB=b-a。△O2O1Cは、直角三角形なので、三平方の定理より、
O2C=O2B-CB=b-a。△O2O1Cは、直角三角形なので、三平方の定理より、 こ~んなにきれいにまとまっちゃうので、これは公式として覚えておけば、とても役にたちますよ。 例えば、平成29年国家一般職(大卒)より。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。
こ~んなにきれいにまとまっちゃうので、これは公式として覚えておけば、とても役にたちますよ。 例えば、平成29年国家一般職(大卒)より。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。 ①4√3②7③8④6√2⑤9 円Aと円Bの半径をrとすると、
①4√3②7③8④6√2⑤9 円Aと円Bの半径をrとすると、 よって、
よって、 正解は、肢③です。 もういっちょう~。平成22年地方上級より。次の図のように、半径3cmの円と半径6cmの円が点Cで接している。2つの円に接する3本の接線の交点をO、A、Bとするとき、ABの長さはどれか。
正解は、肢③です。 もういっちょう~。平成22年地方上級より。次の図のように、半径3cmの円と半径6cmの円が点Cで接している。2つの円に接する3本の接線の交点をO、A、Bとするとき、ABの長さはどれか。 ①3√6cm②6√2cm③9cm④4√6cm⑤6√3cm 円外の1点から引いた2つの接線の長さは等しいので、
①3√6cm②6√2cm③9cm④4√6cm⑤6√3cm 円外の1点から引いた2つの接線の長さは等しいので、 ってな具合で、正解は、肢②です。ここをポチッとお願いします。→
ってな具合で、正解は、肢②です。ここをポチッとお願いします。→にほんブログ村






















※コメント投稿者のブログIDはブログ作成者のみに通知されます