集合④

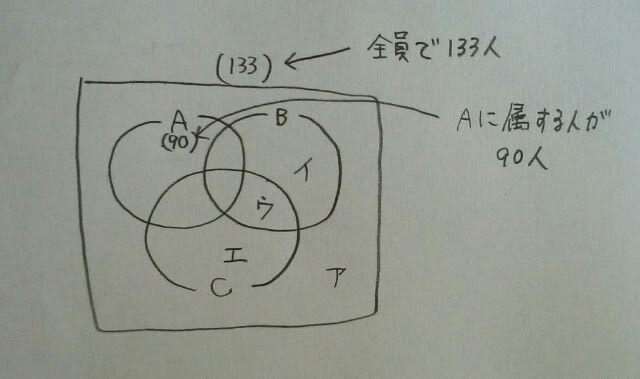
公式が使えないとなると、真っ先に思い浮かぶのが、「くり抜き」という考え方です。例えば、全体の133人から、Aに属する90人をくり抜いて（引いて）しまえば、残りは43人です。つまり、ア＋イ＋ウ＋エ＝43。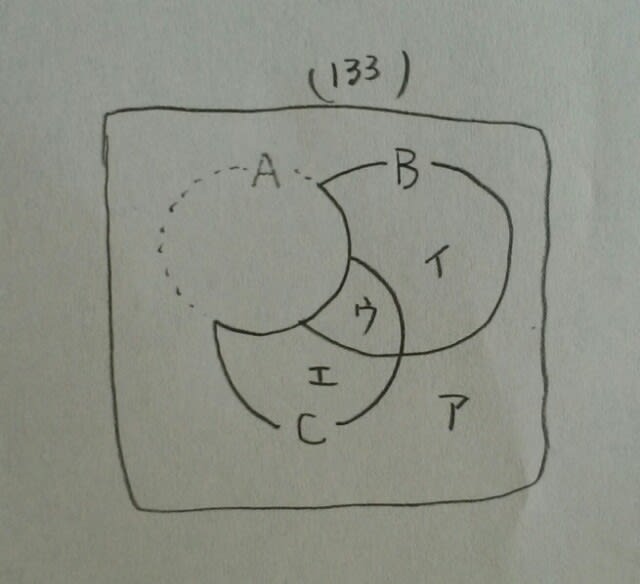例題です。A～Cの問題に生徒133人が取り組んだ。次のような結果が出たとき、確実に言えるのはどれか。　　　　　　　　　　　　　　　　　　　　・3問とも間違えた者は3人であった。　　　　　　　　　　　　　　　　　　　　・Aができた者は90人、AとBのみできた者は21人であった。　　　　　　　　　　　　　　　　　　　　・Bのみできた者はCのみできた者の2倍いて、Aのみできた者より8人多かった。　　　　　　　　　　　　　　　　　　　　・AとCのみできた者は16人で、BとCのみできた者より3人少なかった。　　　　　　　　　　　　　　　　　　　　①Aのみできた者は8人いる。　　　　　　　　　　　　　　　　　　　　②A、C両方できた者は66人いる。　　　　　　　　　　　　　　　　　　　　③A、C少なくともいずれか一つ正解した者は107人いる。　　　　　　　　　　　　　　　　　　　　④Bができた者は全部で101人いる。　　　　　　　　　　　　　　　　　　　　⑤Cができなかった者は52人いる。（平成27年大卒警察官）　　　　　　　　　　　　　　　　　　　　　Cのみできた者がc人いたとすると、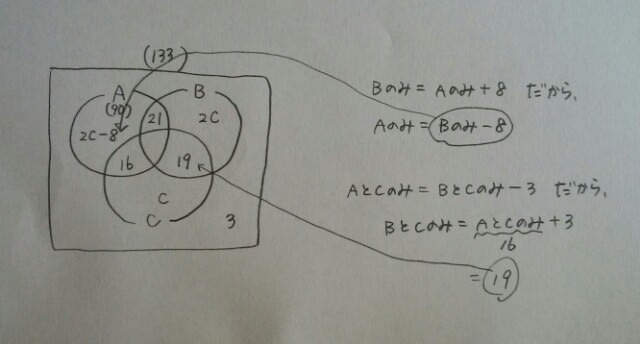Aをくり抜きますと、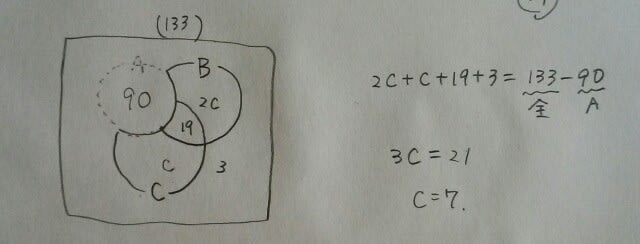元の図にc＝7を代入して、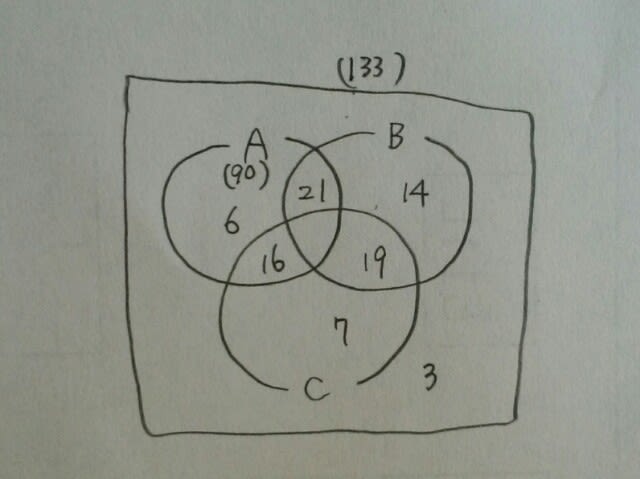3問とも正解した人は、90－21－6－16＝47人。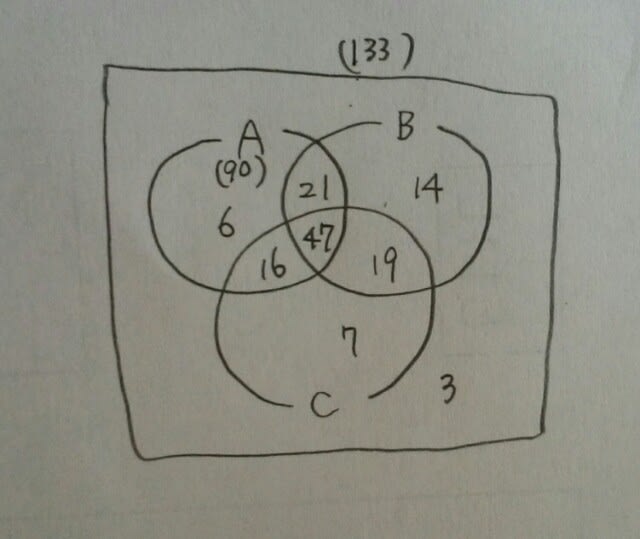肢①Aのみできた者は6人。　　　　　　　　　　　　　　　　　　　肢②A、C両方できた者は16＋47＝63人。　　　　　　　　　　　　　　　　　　　肢③A、C少なくともいずれか一つ正解した者は133－3－14＝116人。　　　　　　　　　　　　　　　　　　　肢④Bができた者は14＋21＋47＋19＝101人。　　　　　　　　　　　　　　　　　　　肢⑤Cができなかった者は133－6－21－14－3＝89人。　　　　　　　　　　　　　　　　　　　正解は、肢④です。　　　　　　　　　　　　　　　　　　　えっ？もう一つやってみたい？ページの下にカテゴリーがあるので、タップして下さい。「もっとみる」をタップ→集合をタップ→警視庁1類から（集合）平成25年9月21日という記事にありますよ。　公式も使えないし、くり抜きもできないときは、どうしたらいいんでしょうか？次へ続く。　　　　　　　　　　　　　　　　　　　ここをポチッとお願いします。→
にほんブログ村この前の台風後、京都鴨川がかなり増水していたとき。四条大橋から撮影。

集合③

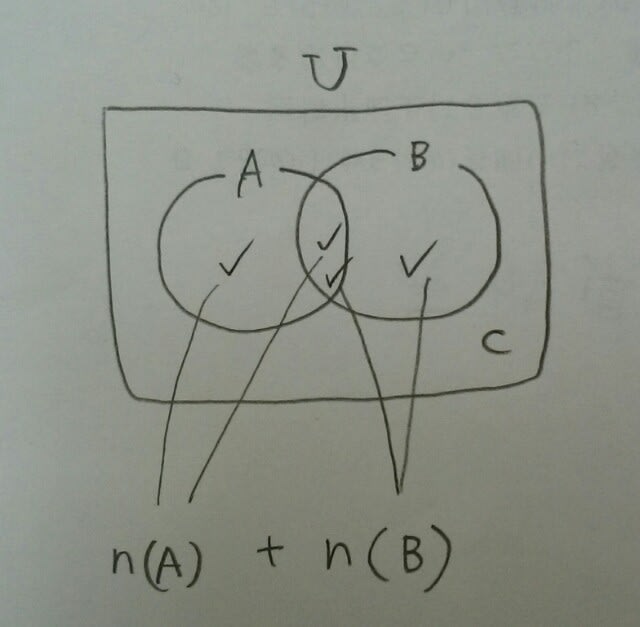
3集合の公式です。2集合の場合と同じように、数えたところに✓をつけます。　　　　　　　　　　　　　　　　　　　まず、n（A）＋n（B）＋n（C）をしてみると、2回数えたり、3回数えたりしたところがありますので、とりあえず、n（A∩B）とn（B∩C）とn（C∩A）を引きます。実際に、消しゴムで消してみて下さい。すると、こうなります。あと、n（A∩B∩C）と、D（AでもBでもCでもないところ）を数えれば、それぞれを1回ずつ数えたことになりますね。ということで、3集合の公式は、　　　　　　　　　　　　　　　　　　n（A）＋n（B）＋n（C）－n（A∩B）－n（B∩C）－n（C∩A）＋n（A∩B∩C）＋n（D）＝n（U）です。　　　　　　　　　　　　　　　　　　　　練習問題です。　　　　　　　　　　　　　　　　　　　　ある旅館で利用客123人に対して、温泉、料理、および眺望のうち何が良かったかについて重複回答を認めた上でアンケート調査を行った結果、次のA～Dのことがわかった。いま、この3つのいずれも良くなかったとする者は何人か。　　　　　　　　　　　　　　　　　　　　A　温泉が良かったとする72人のうち、料理も良かったとする者が53人いた。　　　　　　　　　　　　　　　　　　　　B　料理が良かったとする73人のうち、眺望が良かったとする者が51人いた。　　　　　　　　　　　　　　　　　　　　C　眺望が良かったとする78人のうち、温泉も良かったとする者が49人いた。　　　　　　　　　　　　　　　　　　　　D　この3つのいずれも良かったとする者は、41人であった。　　　　　　　　　　　　　　　　　　　　①12人②13人③14人④15人⑤16人（平成16年大卒警察官）　　　　　　　　　　　　　　　　　　　　Aが温泉、Bが料理、Cが眺望（いずれも良かったとする者の数）として、公式に当てはめて、　　　　　　　　　　　　　　　　　　　　72＋73＋78－53－51－49＋41＋n（D）＝123。これを解いて、n（D）＝12。正解は、肢①です。　　　　　　　　　　　　　　　　　　　　公式を用いる問題が全てではありません。今度は、公式を使わない問題を見ていきます。集合④に続く。ここをポチッとお願いします。→
にほんブログ村

集合②

雑誌読み放題サービスも選べる！【ひかりＴＶブック月額プラン】
2集合の問題を、ベン図で考えます。公式があります。　　　　　　　　　　　　　　　　　　n（A）＋n（B）－n（A∩B）＋n（C）＝n（U）です。　　　　　　　　　　　　　　　　　　n（A）とは、集合Aに含まれる要素の個数。分かりやすくいうと、「Aに何個入ってるか」です。∩は、「かつ」、Cは、AでもBでもないところ、Uは、全体です。　　　　　　　　　　　　　　　　　　n（A）は、集合Aの要素の個数だから、そこに何個あるかを数えたら、忘れないように、チェック（✓）していきます。n（A）＋n（B）をしたら、A∩Bの部分を、2回数えてしまいました。ゆえに、1回引いときましょう。（✓を一つ消す）。そうすると、後、Cの部分を数えると、全ての場所を1回ずつ数えたことになるので、全体の数になりますね。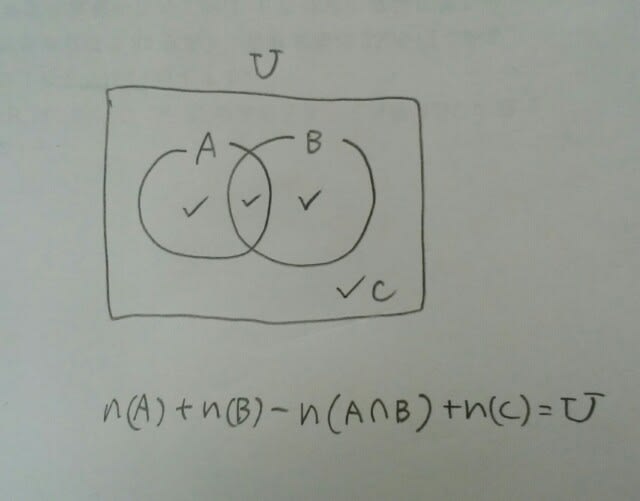これが公式の意味です。そんなこと、当たり前やないかい！と怒られそうですが、これを確認しないと、3集合の公式に行けないのです。一応、公式を使って、次の問題を解いて下さいね。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　45人の団体がある博覧会に行ってきたというので、AパビリオンとBパビリオンを見学したかどうか全員に聞いてみたところ、次のア～ウのことがわかった。Aパビリオンを見学したのは何人か。　　　　　　　　　　　　　　　　　　ア　31人はどちらも見学した。　　　　　　　　　　　　　　　　　　イ　38人はBパビリオンを見学した。　　　　　　　　　　　　　　　　　　ウ　2人はどちらも見学しなかった。　　　　　　　　　　　　　　　　　　　　公式に当てはめて、n（A）＋38－31＋2＝45。よって、n（A）＝36。正解は、36人です。今度は、3集合の公式です。（その③へ）ここをポチッとお願いします。→
にほんブログ村

集合①

34人の生徒について、兄姉の有無を調べたところ、兄がいる生徒は13人、姉がいる生徒は15人、兄も姉もいない生徒は14人であった。兄だけがいる生徒は何人ですか。　　　　　　　　　　　　　　　　　　　　①5人②6人③7人④8人⑤9人（長野県教員採用試験）　　　　　　　　　　　　　　　　　　　　兄がいるかどうか？姉がいるかどうか？の2集合の問題です。2集合なら、表に整理すればよいのです。そして、どんどん引き算します。よって、正解は、肢①です。こんなのは、簡単ですね。　　　　　　　　　　　　　　　　　　
　一応、練習問題です。福岡県の教員採用試験から。　　　　　　　　　　　　　　　　　
　学生50人がいるクラスがある。クラスの中でピアノが弾ける人が20人、ギターが弾ける人が25人、ピアノもギターも弾けない人が20人いるとき、ピアノは弾けるがギターが弾けない人が何人いるかを求め、下の①～⑤から一つ選びなさい。　　　　　　　
①5人②8人③10人④12人⑤15人（正解は、動物画像の下）。　　　　　　　　　　　　
さて、2集合ならこれでよいのですが、3集合なら、ベン図やキャロル図が必要です。公式もあります。そのための準備として、2集合の問題を、ベン図を使って考えてみます。（その②へ続く）ここをポチッとお願いします。→
にほんブログ村正解肢①

警視庁3類no39（平成28年9月18日）

　　

　　LECオンラインショップ（Ｅ学習センター）
　　　あるフルマラソン大会を完走した男女1000人について調査したところ、次のア～エのことがわかった。このとき、外国人の女性で完走タイム5時間未満の者と日本人の男性で完走タイム5時間未満の者の総数として、最も妥当なのはどれか。　　　　　　　　　　　　　　　　　　ア　男性は600人であり、女性は400人であった。　　　　　　　　　　　　　　　　　　イ　日本人の人数は560人で、そのうち320人は女性であった。　　　　　　　　　　　　　　　　　　ウ　完走タイム5時間未満の人は500人で、そのうち180人は外国人であった。　　　　　　　　　　　　　　　　　　エ　完走タイム5時間以上の人のうち、160人は女性であり、100人は日本人の男性であった。　　　　　　　　　　　　　　　　　　①160人②180人③200人④220人⑤240人　　　　　　　　　　　　　　　　　　　　キャロル図に、条件の人数を書き込んでいきます。日本人が560人なので、外国人は440人です。日本人の男性で完走タイムが5時間未満の者は、次のようにして、140人です。次に、5時間未満の者が５００人なので、さらに、女性が400人なので、外国人の女性で5時間未満の者は60人と分かりました。よって、求める数は、60＋140＝200人。正解は、肢③です。