雑誌読み放題サービスも選べる!【ひかりTVブック月額プラン】
 2集合の問題を、ベン図で考えます。公式があります。 n(A)+n(B)-n(A∩B)+n(C)=n(U)です。 n(A)とは、集合Aに含まれる要素の個数。分かりやすくいうと、「Aに何個入ってるか」です。∩は、「かつ」、Cは、AでもBでもないところ、Uは、全体です。 n(A)は、集合Aの要素の個数だから、そこに何個あるかを数えたら、忘れないように、チェック(✓)していきます。
2集合の問題を、ベン図で考えます。公式があります。 n(A)+n(B)-n(A∩B)+n(C)=n(U)です。 n(A)とは、集合Aに含まれる要素の個数。分かりやすくいうと、「Aに何個入ってるか」です。∩は、「かつ」、Cは、AでもBでもないところ、Uは、全体です。 n(A)は、集合Aの要素の個数だから、そこに何個あるかを数えたら、忘れないように、チェック(✓)していきます。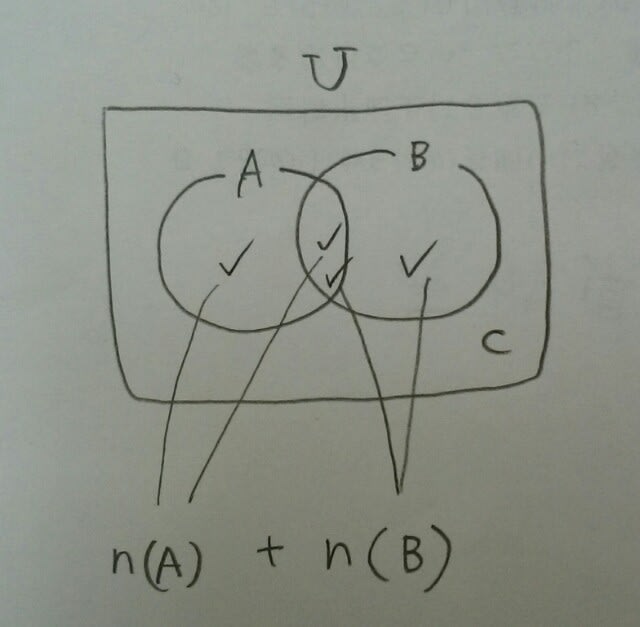 n(A)+n(B)をしたら、A∩Bの部分を、2回数えてしまいました。ゆえに、1回引いときましょう。(✓を一つ消す)。
n(A)+n(B)をしたら、A∩Bの部分を、2回数えてしまいました。ゆえに、1回引いときましょう。(✓を一つ消す)。 そうすると、後、Cの部分を数えると、全ての場所を1回ずつ数えたことになるので、全体の数になりますね。
そうすると、後、Cの部分を数えると、全ての場所を1回ずつ数えたことになるので、全体の数になりますね。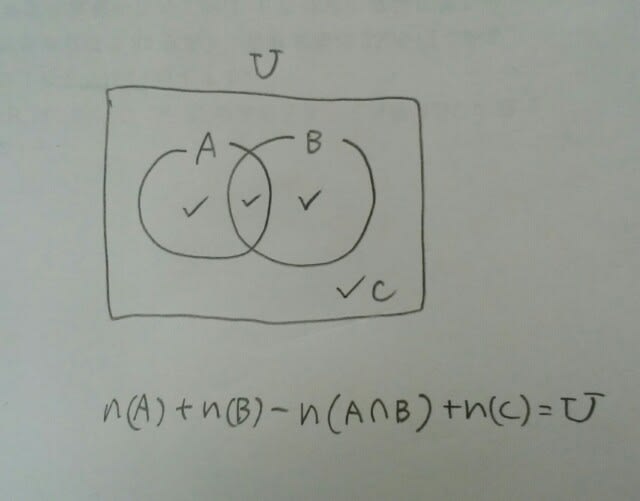 これが公式の意味です。そんなこと、当たり前やないかい!と怒られそうですが、これを確認しないと、3集合の公式に行けないのです。一応、公式を使って、次の問題を解いて下さいね。 45人の団体がある博覧会に行ってきたというので、AパビリオンとBパビリオンを見学したかどうか全員に聞いてみたところ、次のア~ウのことがわかった。Aパビリオンを見学したのは何人か。 ア 31人はどちらも見学した。 イ 38人はBパビリオンを見学した。 ウ 2人はどちらも見学しなかった。 公式に当てはめて、n(A)+38-31+2=45。よって、n(A)=36。正解は、36人です。今度は、3集合の公式です。(その③へ)ここをポチッとお願いします。→
これが公式の意味です。そんなこと、当たり前やないかい!と怒られそうですが、これを確認しないと、3集合の公式に行けないのです。一応、公式を使って、次の問題を解いて下さいね。 45人の団体がある博覧会に行ってきたというので、AパビリオンとBパビリオンを見学したかどうか全員に聞いてみたところ、次のア~ウのことがわかった。Aパビリオンを見学したのは何人か。 ア 31人はどちらも見学した。 イ 38人はBパビリオンを見学した。 ウ 2人はどちらも見学しなかった。 公式に当てはめて、n(A)+38-31+2=45。よって、n(A)=36。正解は、36人です。今度は、3集合の公式です。(その③へ)ここをポチッとお願いします。→
にほんブログ村

 n(A)+n(B)をしたら、A∩Bの部分を、2回数えてしまいました。ゆえに、1回引いときましょう。(✓を一つ消す)。
n(A)+n(B)をしたら、A∩Bの部分を、2回数えてしまいました。ゆえに、1回引いときましょう。(✓を一つ消す)。 そうすると、後、Cの部分を数えると、全ての場所を1回ずつ数えたことになるので、全体の数になりますね。
そうすると、後、Cの部分を数えると、全ての場所を1回ずつ数えたことになるので、全体の数になりますね。 これが公式の意味です。そんなこと、当たり前やないかい!と怒られそうですが、これを確認しないと、3集合の公式に行けないのです。一応、公式を使って、次の問題を解いて下さいね。 45人の団体がある博覧会に行ってきたというので、AパビリオンとBパビリオンを見学したかどうか全員に聞いてみたところ、次のア~ウのことがわかった。Aパビリオンを見学したのは何人か。 ア 31人はどちらも見学した。 イ 38人はBパビリオンを見学した。 ウ 2人はどちらも見学しなかった。 公式に当てはめて、n(A)+38-31+2=45。よって、n(A)=36。正解は、36人です。今度は、3集合の公式です。(その③へ)ここをポチッとお願いします。→
これが公式の意味です。そんなこと、当たり前やないかい!と怒られそうですが、これを確認しないと、3集合の公式に行けないのです。一応、公式を使って、次の問題を解いて下さいね。 45人の団体がある博覧会に行ってきたというので、AパビリオンとBパビリオンを見学したかどうか全員に聞いてみたところ、次のア~ウのことがわかった。Aパビリオンを見学したのは何人か。 ア 31人はどちらも見学した。 イ 38人はBパビリオンを見学した。 ウ 2人はどちらも見学しなかった。 公式に当てはめて、n(A)+38-31+2=45。よって、n(A)=36。正解は、36人です。今度は、3集合の公式です。(その③へ)ここをポチッとお願いします。→にほんブログ村






















※コメント投稿者のブログIDはブログ作成者のみに通知されます