xyzzy に侮られる。

xyzzy を導入したので，ほんの少しだけ遊んでみた。

とりあえず LaTeX ファイルを編集できるようになったら嬉しいな，と考えて，設定メニューを探していたら，ツールに (>_<) という可愛らしい顔文字があったので，迷わずそれを開いてみる。

すると，ハノイの塔やら五目並べやら，確か本家の Emacs にもあったメニューが並んでいた。

まずハノイの塔を選ぶと，7 段のハノイの塔が，円板がパタパタと移動するアニメーション付きであれよあれよという間に解かれていく。

もしかすると段数もある程度選べるのかもしれないが，それはともかくとして，これらの機能は M-x で実行することができる。

Meta キーという UNIX 系のキーボードに備わっていたキーは Windows 用のものにはついていないが，通常，Alt キーを Meta キーとして使えるような設定（キーバインド）が用いられる。

xyzzy も，もとからそのキーバインドになっている。そこで，M-x と押すと，バッファウィンドウというところに M-x: と表示されるので，そのまま gomoku と打ち込む。

そうすると五目並べ―モードが発動し，小さいポップアップウィンドウ（いうなれば吹き出し）に，英語表記ではあるが，「私に先手を譲ってくれますか？」と対戦相手であるコンピュータからの申し入れが表示される。

仕方がないなぁということで，Yes を選択すると，先手側のコンピュータが嬉しそうに O を打ち込む。

後手の私はカーソルで石を打つ場所を選んで X を打ち込む。

五目並べというのは，私の感想としては，後手が先手に振り回されるゲームである。ちょっとぼんやりしていると両端の空いた「三」が作られ，打つ手を間違えると両端の空いた「四」へと成長し，その次のこちらのターンでこちらが五目を完成させる見込みがなければ，つまり，相手が自分の手を完成させることを優先してこちらのリーチを見逃してくれていないかぎり，相手の「四」が盤面に登場した時点でこちらの負けが確定する。

気を付けて差し手を考えているつもりだったが，あやしい飛び四が現れたときに，その間を埋めれば五目が完成することに気付かず，別のところに指してしまった。

その結果，全部で 10 手もいかないくらいで一局が終了したわけだが，エコー領域と呼ばれる部分に「弱すぎ！」とこちらをディスるメッセージが表示されたのを私は見逃さなかった。

先手は譲ったものの，勝ちまで譲るつもりはなかったのだが，致し方ない。

三×三のマス目に〇と×を交互に並べていくスタイルでおなじみの三目並べは先手と後手が互いに最善手を指し続けると引き分けになる。

これは経験上，誰しも感じていることであろう。

それでは五目並べも同じように引き分けになるゲームなのであろうか。

先ほども述べたが，私にとって五目並べは先手が次々と五目を完成させようと仕掛けてくるのを，後手が神経を削りながら，文字通り後手に回りつつ阻止するゲームであって，後手が先手を出し抜いて下剋上を果たすのは極めて望みが薄いように感じている。

自分が先手であるとき，差し回しが下手だとダラダラと続いてしまうが，ちょっと気を付けいれば後手の企みはことごとく潰すことができる。

逆に自分が後手であるときは，先手が次から次へと対応を迫ってくるため，いつ罠にかけられるかとビクビクして落ち着かない。そんな気色悪さがある。

Wikipedia で確認したところ，禁じ手がないルールだと先手必勝であることが，明治時代，1899 年に黒岩涙香という人が必勝法を発見したことで判明しているとのことである。

そういや，つい最近，オセロは引き分けゲームらしいというのがコンピュータの支援の下で検証されたというニュースがあったっけな。

1899 年といえば，私がすぐ思い浮かべるのは David Hilbert が Grundlagen der Geometrie（幾何学の基礎）という著作を発表した年である，ということくらいである。

それとは関係ないが，Giuseppe Peano が，今日 Peano の公理系の名で呼ばれる，1 のすぐ次の数は 2，2 のすぐ次の数は 3，といったような，カウント（数える）という行為に根差していると思われるスタイルで自然数とはどういう体系であるのかを数学的に明快に特徴付けた理論を Arithmetices Principia という書籍で出版したのが 1889 年，自然数から実数に至るまでの道筋を数学的に示して見せた Richard Dedekind の Was sind und was sollen die Zahlen?（数とは何ぞや，そして其は何であるべきぞや）の 1888 年の登場にタッチの差で及ばなかったところであった。

それもまた別の話。

ところで，本家の GNU Emacs の最新版は 2044 年 3 月 27 日付けの GNU Emacs-29.3 のようだが，あえて xyzzy を利用しようとせず，素直に本家の方を導入する方が良いのではないか，と言われれば，まったくもっておっしゃる通りである。

だが，本家が提供してくれる超高機能な統合開発環境を使い倒すのではなく，ほんのちょっと出来心で Emacs LISP をいじってみたい，という軽い遊び程度なら，日本で生まれた xyzzy がとても手軽でお手頃のように思うのである。

今のところ，xyzzy の設定を elisp ファイルだっけ，そういうのをちゃんと作って行おうとか，本家をインストールして，腰を据えて使おうとか，そこまで大事には考えていない。

春休みがもう終わってしまったので，これから 4 か月ほどは遊べなくなってしまうし。

この春休みは，今年こそじっくり勉強するぞと思っていたのに，何もせずに，何もなせずに，いたずらに時間が過ぎてしまった。毎年繰り返していることは今年も起こる。そうか，それを数学的帰納法と人は呼ぶのだな。

Wikipedia の気になる記事に手を入れてみようとか，日本語版がまだない項目のいくつかを，英語版を翻訳して立ててみようかと夢を抱いていたが，ちょくちょく誤植と思われる個所を訂正したり，リンク切れになっているところを，移動先の URL に貼り直したりといった保守作業をちまちまやっただけで終わった。

最近興味が再燃した CASL II も今やオワコンだし，xyzzy も最後の版から 10 年が経過しているし，それでもどちらも Windows 11 で使えるよ，といった簡単な報告に終始したわけだが，それが私という人間の嘘偽りのない能力そのものなのだから，受け入れることとしよう。

それでは，思い出の一枚を添付して筆を擱く。

xyzzy の編集画面を Ctrl+x 2 で上下 2 段に画面を分割し，上の画面には LaTeX 文書（ファイル名は test.tex）をべた書きし，下の画面で M-x shell で何か（おそらくコマンドプロンプトという名称の，cmd.exe）を起動し，ファイルを編集しているフォルダが作業フォルダとなっているので，そのまま

>platex test

と打ち込んでコンパイルし，コンパイルが通れば test.dvi というファイルが生成されているので，それを

>dviout test

で閲覧すると，DVIOUT というプレヴューアの別ウィンドウが開いてそれが表示される，といった流れである。

xyzzy と DVIOUT のウィンドウを仲良く並べて撮影した記念撮影がこちら。↓
春休み最後の日の思ひ出。
Windows キー+Shift+S で，はい，チーズ！（パシャリ）



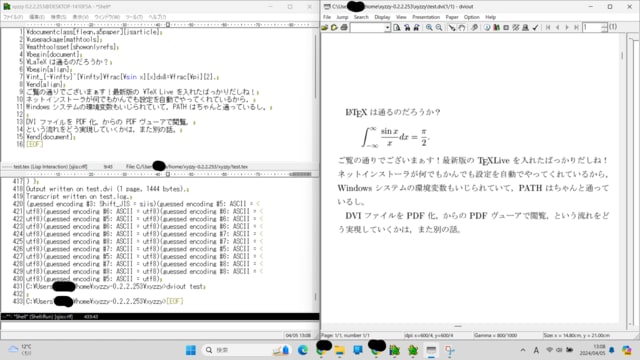
あ，積分の中の dx の前に \, で小さな空白を入れるのを忘れていたけど，まあ，五目並べにあっさり負けたくらいぼさっとしているので，ご愛敬ということで。

xyzzy という Emacs 風のアプリ。

Windows で LISP を体験してみたい。

人がそんな想いを抱いた時，取るべきアクションは何か。

ブラウザを開いて検索ウィンドウに「Windows LISP」と入力するだけで，あとは検索結果に従えば，しばらくしてその夢は実現するであろう。

平素より私が言葉にできないほどお世話になっている I 先生が Windows で LISP を触ってみたいときにどうすればよいか，という話題になった時に，なんとおっしゃっていたか，記憶はおぼろげである。

だが，キーワードとして

xyzzy という Emacs 風のエディタ，

Maxima（Windows で使うのは wxMaxima という名称である）という数式処理ソフト

が挙がったのは間違いない。

今回は xyzzy が Windows 11 でも動作したよ，というお話である。

20 年以上前，私は学部 4 年生のときに研究室に配属されたのをきっかけに数式組版ソフトの LaTeX を使い始めたのだが，当時は大学で使用されている端末は UNIX と Windows がしのぎを削っており，しだいに Windows が優勢になってきていた時代であった。DEC 10 Prolog と呼ばれるものにちょこっとだけ触れたのも，今にして思えばちょうど最後らへんのことだったようである。その DEC 10 なるものは PDP-10 のことであり，最近，別のルートから PDP-8 だの PDP-11 だのとの関連で再会した名前である。

私が所属した研究室では，ちょうどその狭間のような感じで，広く出回るようになった Linux 環境が提供されていた。

LaTeX の文書は Linux 上で動く究極のエディタ Emacs の支援の下で作成していた。

私も Linux をほんの少しだけかじったが，それは要するに bash だかなんだかのシェルのコマンドをちょこっと学んだというだけの意味であって，kernel だのなんだのをいじったとかそういう話では全くない。

それはともかくとして，やはり時代は Windows の風が吹いており，Windows 上で Emacs 環境が使えたらなぁ，と思っていた矢先，もちろん本家の Emacs も使おうと思えば使えたようだが，Linux で実際にお世話になっていた Mule（ミュール）という日本語が使いやすくなっている多言語拡張版を Windows に移植した Meadow（メドウ，確か Mule for Windows というのが本来の名前であった）が現れたところで，大変お世話になった。

そのころ，今から 20 年ほど前の話なわけであるが，それから今日に至るまでの間，私はずっと Meadow を使っていたわけではない。Meadow の開発は 20 年ほど前のその頃に止まってしまい，こちらはこちらで Windows のバージョンが数年おきに更新され，使う PC もやはり代替わりしていく中で，エディタは別のを使うようになっていった。

といいつつ，実際にその間，どんなので TeX ファイルを作成していたのか，思い出せない。結局海外製の，日本語が編集画面で微妙に文字化けするような，なんかそういうのを使っていたのは覚えている。それは今使用している TeXworks とよく似たものだったが，それそのものではなかったような気がする。そこがはっきり思い出せない。

こんな感じの遍歴をしてきたわけだが，Meadow がうまく使えなくなった時，代替案として xyzzy の利用も検討したのだが，TeX のコマンド補充支援でお世話になっていた YaTeX（野鳥，やてふと読む。Yet Another Tex Mode）がうまく動かないんだったか，M-x のキーバインドがうまく使えなかったんだか，使い辛くて採用を見送った覚えがある。

今回は久々に xyzzy のことを思い出してまだネットに落ちているか調べてみたが，作者の亀井哲弥さんの跡を継いで有志が保守して下さっていたことが判明した。

といっても，それは 2013 年頃までのことだったようで，それから 10 年が経つ今，そのプロジェクトがどうなっているのかは不明である。

窓の杜経由でダウンロードしたバージョン 0.2.2.253 は 2024 年 4 月現在，Windows 11 もちゃんと動くみたいだ，というのが今回一番書きたかったことである。

「する」モノと「される」モノ。

数の計算というのは四則演算と呼ばれる，足す，引く，掛ける，割る，という四種類の計算規則が基本ということになっている。

それらはいずれも 2 つの数をそれぞれの意味合いで合わせることで，何がしかの 1 つの数を生み出す操作であるというのが通常の理解の仕方であろう。

それは，2 つの数を入力すると，計算結果の数が 1 つ出力される働きであって，数学ではそのようなものを 2 変数関数と呼ぶ。

今から 30 年ほどの昔，私が学部学生であった頃は，Peano の公理系によって自然数とは何なのかが明確に定められ，それを足掛かりにして，整数，有理数，そして実数へと数の世界を拡張していく，いわゆる「厳密な理論展開」の存在を知り，当時の私には何故だか非常に魅力的な理論体系に思えて強い憧れを抱いたものである。

その憧れは色あせていない。というか，白状すれば，そういったシナリオに従って数体系を拡張していく議論に，その 30 年もの間さぼっていて，真面目に取り組んでこなかった。

まあ，大体のストーリーは抑えているような気がするので，それでひとまず満足してしまっているというのが嘘偽りのない現状である。

当時，大学の図書館で漁った書籍の一冊に，竹内啓さんの『数の構造』（教育出版，1976 年）があった。そのまえがきに，数の演算，例えば加法 a+b を，a と b という二つの数を平等に扱って，それらから生み出された 1 つの数を対応させる，いわゆる「二項演算」とみるのが通常行われていることであるが，これを，a に b を追加する，というような「操作」として扱う立場も大切ではないか，といったような主旨の話が述べられており，同書はその立場で数の体系を論じたものだと書かれていた。

そのまえがきだけに目を通したままであるが，初めて読んだ当時の私は完全に二項演算派であって，「なんでそれをわざわざ a に b を追加する，なんていう見方にするんだろう」と違和感を覚え，竹内啓さんの観点に乗っかって同書を読み進める気が起きなかった。とはいえ，そういう観点があるということをそこで教わったわけであるし，今日に至るまでなんとなくずっと気になってはいる。

ちょうどその本が出版されたちょうどその頃，算数教育において「量の概念」の復権を掲げて日本の初等数学教育をけん引してきた遠山啓さんの健康にかげりが見えていたわけであるが，そんな中，小島順さんが日本放送出版会から『線型代数』という，これまたユニークな本を出版し，それが火種となって日本評論社の『数学セミナー』誌上で「量の問題をめぐって」というリレー連載が始まった。その中で，1978 年 8 月号から 12 月号まで，5 回に渡って同連載を担当されたのが竹内啓さんであった。遠山啓さんは 1979 年に亡くなったが，病床にあってこれらの連載のことをご存じだったのか，また，もしご存じだった場合，そうそうたる執筆者たちが展開する論説をどうご覧になったのか，などが気になってならない。


そのあたりの話は置いておいて，私はこのところ，数の演算について，2 つの数を平等に扱う「二項演算派」から，数直線において，座標 a で示されている点を，数 b が表す量だけ平行移動する，といった幾何学的な運動，つまりは操作という見方に傾きつつある。

日本語では

「a と b を足し合わせる」

と言えば，a と b の間に役割の区別はない平等な二項演算派の下での扱いに感じられるのに対し，

「a に b を加える／足す」

というと，絶対座標 a に，平行移動 +b を施す，といった操作に感じられるのである。

この話は，複素数の積が複素平面において回転操作と解釈できることの意味をじっくり考察したいとここ数年思い始めたことが根っこにあるのだが，その話も置いておいて，アセンブリ言語をかじると 2 つの側面でこういったことを意識してしまうのである。

一つは，命令（コマンド）というものの書式が，例えば英語の命令文と同様の構文になっており，

操作名（間をあけて）操作対象

と記述するのが一般的なのだが，英語では「操作するモノ」を operator，「操作されるモノ」を operand と呼ぶ。ポイントは，こういった言い回しがちゃんとあるという点である。

さて，2023 年 4 月以降の試験問題からさよならしてしまった，基本情報技術者試験午後試験の選択できるプログラミング言語のひとつであった，その試験用に特別に用意された CASL II というアセンブリ言語が実際に動く web 上のシミュレータがいくつか現存しており，ごく簡単なプログラムを作ってみては動作確認をして遊んで春休み気分を思いっきり満喫している今日この頃なのであるが，久々に 1 から 100 までの整数の和を求めるプログラムを試してみようと思いついた。

アセンブリ言語ではプログラムの行にラベルと呼ばれる名称を割り振って，必要に応じてその行に翔んで（さい〇ま）作業をさせる必要がある。CASL II の仕様では，ラベルは英大文字から始め，続きは英大文字と数字のいずれを使ってもよいが，8 文字以内に収めよ，という制約がある。

その中で，カウンタ番号を一つ増やした上で，それをすでに求めてある和にさらに追加する操作を，例えばカウンタ番号が 100 になるまで繰り返させる（100 になった状態で最後に追加してから繰り返し操作を打ち切る）手続きを記述するわけであるが，さて，その繰り返し処理（ループ，ブロック）の入り口などにどんな名前を付けるといいのか，と考えると，カッコイイ，ドンピシャな英単語を知っていれば解決するのだが，私のように知らないと名付けが悩みの種となる。

ちょうどシミュレータをネット上で漁っていた時，異なる言語だったと思うが，それで同じように 1 から 100 までの和を求めるプログラムを書いたらこんな感じになる，といったブログ記事がヒットし，ざっと眺めていたら，確か addend という語が名に入った。

これは，足し算を

（被加数）＋（加数）

と捉える見方に由来する呼び名で，a+b の a と b はある意味平等ではなく，a は augend（被加数），b は addend（加数）という役割が割り振られている。

式で表すと

augend ＋ addend ＝ sum（和）

ということであろうが，左辺の各項は summand（加算項）とも呼ばれるそうだ。

operator(operand) の記法にするには，例えば +b(a) とでも書くべきかもしれない。これだとポーランド記法にそっくりだが，その考案者の Łukasiewicz（ウカシェヴィチ）さんは カッコから解き放たれた (parenthesis-free) 数式の記法を編み出そうとしたそうなので，私のようにカッコを付けて書くなどもってのほかであろうが。

掛け算では「乗数」（掛ける数）を multiplier というが，私の専門分野ということになっている解析学畑では Lagrange multiplier とか Fourier multiplier といった名称で馴染み深い。

これは

multiplicand（被乗数）× multiplier（乗数）＝ product（生成されたモノ，積）

のようになっている。

割り算はと調べると，割る数（除数）が divisor だというのはすぐに見当がつく。割られる数（被除数）の英語名は知らなかったが，dividend だそうである。

数式で表せば

dividend ÷ divisor ＝ quotient（商）

である。引き算 (subtraction) はある意味異質で，

minuend － subtrahend ＝ difference（差）

となる。minus 由来と subtract 由来の語がまぜこぜになっている。

ヨーロッパ言語の特徴なのかどうかは知らないが，英語を習うと動詞の能動態と受動態の区別を意識せざるを得なくなる。

演算を 2 つの数に関する加工作業と考えた場合，動作主（ぬし）と，動作の受け手という役割分担が発生することになる。

足し算は，2 つの箱の中身を一つにまとめる合併という捉え方もできるし，一方の箱の中身を他方の箱にあける，といった追加という捉え方もできる。

こうした話は特に初等教育において数の計算が身近なたとえでいうとどんな場面で生じるか，といったことを教える側があらかじめよく分析しておき，整理して児童に教えようとすると生じるものと思われる。

Newton が著した，当時の数学の最先端技法のひとつであった文字式を立ててさまざまな問題を解決するという，ある意味，数学の実用書のはしりと言ってよさげな Arithmetica Universalis（無理に訳せば普遍算術，万能算術とでもなろうか。幅広く通用する算術，といった気持ちが込められていると勝手に推測している。片仮名で読みを書くと，アリトメーティカ・ウニウェルサーリスかな？）ではそのあたりの解説があるのかないのか，ふとこの書の存在を思い出し，気になった次第である。

英語訳がネットに落ちていたような記憶を頼りに検索してみたら，Cambridge 大学が公開している Newton の直筆草稿 がヒットした。マニア垂涎の代物がこうして惜しげもなくネット上でさらされているとは。誠に僥倖哉！

ローマ数字の小数表示。

大学の学部 1 年生に微分積分学を教えるといっても，そもそも理工系の学部・学科であるため，高校の「数学 III」を履修している学生がほとんどである。

にもかかわらず，例えば 50 人のクラスであったとして，そのうちの 1 人か 2 人は「数学 III」をまともに履修していない状態のまま入学する。

そのような学生に対して，入学前に「数学 III」相当の内容を自習するよう，大学側から何らかの指示が出ているという噂は聞いたような気もするが，私のような非常勤講師に公式にそこら辺の事情が伝達されることはない。

私が担当するのは非数学系といおうか，ともかく，いわゆる「数学科」のような数学ガチ勢とは全く異なる工学系のクラスなので，そもそも微分積分学のどういった話題を講義内容として提供し，そのコースを受講する中で身に付けてもらうべきなのか，正直さっぱり分からない。

とりあえず避けるべきは数列や関数の極限の ε-δ 論法的な取り扱いであろう。ε-δ 論法というのは安定的な動作が求められる工業製品づくりには欠かせない哲学というか思想を含んでいるように感じるのだが，その議論の型だけを特訓する科目ならばいざ知らず，メインコンテンツは具体的な関数の微分や積分の計算にあるとするならば，下手に受講生を悩ませ，不安に陥れたり，中途半端な扱いゆえまったく未消化のまま，貴重な講義時間をいたずらに消費しただけで終わってしまうことが目に見えている ε-δ には一切触れずに切り抜けるのが賢い在り方であろうか。

ところがそうすると，題材が 1 変数関数の微分積分に留まる限り，高校の「数学 III」との差別化を図ることが極めて困難になる。

私が長年担当してきた微分積分学の講義においては，高校の「数学 III」に次のように数本毛が生えた程度の話題を提供するにとどまっている。

・有界な単調数列が何らかの極限に収束する（有界単調列は収束列である）ことを実数列が持つ基本性質として認めることにする。

・逆三角関数を明示的に定義し，その導関数を覚えてもらう。

・2 つの関数の積の高次導関数に関する微分公式（いわゆる Leibniz's rule）の紹介。

・べき関数，指数関数，対数関数，三角関数の第 n 次導関数を取り扱う。

・不定形の極限を求める際に便利な de l'Hôpital の規則の紹介。

・関数の Taylor 多項式および MacLaurin 多項式を導入し，関数のべき級数展開について触れる。

・今後，1/√(1-x^2) の不定積分は arcsin(x)，1/(1+x^2) の不定積分は arctan(x) と書いていいからね，という許可を出す。

・いわゆる広義積分の入門的な取り扱い。

こうしてリストアップすると結構毛がふさふさになってきた印象であるが，教わる側も，教える側も，これらの知識が学生にとって将来どう必要になるのか何のビジョンも持たぬまま，既存の薄いテキストの内容をさらに味がまったくわからなくなるまで薄めて提供するだけで 14 週の授業を終える。

ただし，教えている側も，教わる側も，その 14 週はジェットコースターのような目まぐるしい日々を駆け抜けることとなる。

学科ごとの特性に合わせて，例えば情報系ならアルゴリズムの計算量を解析的に見積もるなんていうモチベーションでオーダー記法と呼ばれるものを特訓するとか，学生が学科の専門科目ですぐに要求されるであろう数理的な知識や技能の下準備として微分積分学の必要そうな部分に特化して 14 週を過ごすのが合理的とは思うのだが，さまざまな事情でなかなかそういうわけにもいかないのが現状である。

それで何を言いたかったのかというと，かつて月刊誌『数学セミナー』で前原昭二さんが 1971 年 7 月号から 1972 年 8 月号までの 14 回にわたって「基礎講座 数 IV 方式 微分積分」というタイトルで連載されていた。私はそれで「数 IV 方式」なる言葉を知ったのだが，第 1 回の「はじめに」で

数 IV 方式とは不精者の数学である．

という，著者自身がどこかで聞いた言葉として紹介されている。その意味は不精者にも分かるような（やさしい）数学という意味ではなく，高校の「数学 III」で習った知識を前提として，つまり，教える側がそれらの知識の再確認をさぼって，その先に続く内容を大学初年級の学生に教えるという意味で，不精者なのは教師の方だという解釈が付されている。

ところが，当時から「数 IV 方式」なる言葉が世に存在したにも関わらず，本気でそのような路線を推し進めた大学初年級対象の微分積分学の教科書を著者は見たことがなく，そのため，試みにこんな内容であろうかという試論を連載で展開してみる，といった話である。

なお，その記念すべき初回の内容は，部分積分を繰り返して関数のテイラー級数展開を得るもので，部分積分にはそんな使い方があるんだと学生の興味を引き立てるだけでなく，それから「超高校級」であるテイラー展開という大学微分積分学の花形ともいえる重要な内容にすぐ手が届くところがミソであるように思う。

その後の展開はというと，テイラー展開ときたら複素関数論でしょ，といわんばかりで，結局は 1 変数の複素関数論への入門コースといった内容になっている。

とはいえ，途中で定積分の台形公式やシンプソンの公式の誤差評価を試みたり，テイラー展開を通じて Euler の公式 e^iθ=cosθ+isinθ を導き，それを単振動の微分方程式と絡め，複素平面上での質点の運動を論じ，中心力場での 2 体問題を解き，平面曲線の曲率について触れている。そして最後に再び Euler の公式に戻って逆三角関数と対数関数の話に戻り，Riemann 面の話まであと一歩，というところで連載を終えている。

思い返してみると私の高校時代は「数学 II／数学 III」ではなくて「基礎解析／微分・積分」だった時代なのだが，ともかくまだ微分方程式の初歩，特に変数分離形の解法と，「水の問題」に代表されるような文章題から自分で微分方程式を立てて解くことは正規の課程の一つであったし，「微分・積分」の教科書には台形公式がコラムで紹介され，教科書傍用の問題集にはシンプソンの公式までもが参考として記載されていた。ただし，複素（数）平面の扱いはなく，それは私の数年後の代から，確か「数学 B」の一分野として復活した。

前原昭二さんの「数 IV 方式 微分積分」は，ご本人曰く，最終回の記事の末尾に，「いつの間にか <複素数&rt; の宣伝文書みたいになってしま」ったとか，「とりとめのない話」と自己批判というか反省の弁を述べられているが，「数学 III」で学んだであろう微分方程式や複素平面とのつながりを大学初年級の学生に披露することは，彼らがその後，さらなる（解法中心の）微分方程式論や複素関数論（の初歩）を学ぶであることを考えると，新入生向けのオリエンテーション的な科目という位置付けならばうってつけの話題の選び方であろう。

ある意味，高校の「数学 III」ではそこまで持っていきたいけれども，さすがにそれは無理かと断念せざるを得なかった，目の前にあるのに手の届かない話題のオンパレードであって，高校と大学の橋渡し的な講義はあるべき健全な姿であるようにも思うのである。

似たような試みは前原先生以前からも，またその後も今日に至るまで多くの大学教師が模索してきたであろうが，寡聞にしてこれといった決定打に出会ったことはないような気がする。

今回，日本評論社の公式サイトで提供されている検索サービスで前原先生の記事を調べようとしたが，「数 IV 方式」というキーワードではうまく引っかからなかった。
仕方がないので著者名で検索してようやくたどり着いたのだが，日本評論社のデータベースではタイトルが「数４方式 微分積分」のようにローマ数字の IV ではなくてアラビア数字（のいわゆる全角であろう）４に変更されている。それが検索がうまくいかなかった原因のようである。

ちなみに，同社から 2016 年に出版されている三町勝久氏の『微分積分講義 [改訂版]』という書籍の内容紹介に「数 IV 方式」という言葉が含まれていたため，それが検索でヒットしたのだが，そちらは「高校の数 III で 1 変数関数の微分積分は十分学んだでしょ」ということで，多変数関数の微分積分に進むという方向性のものであるようだ。

私が学部 4 年生のときに所属した研究室の先輩にも同様の方針を実践している方がいたのを思い出す。理工系の大学 1 年生相手に 1 変数関数の微分積分を繰り返しても教わる側にとっては新鮮味が欠けていてモチベーションが上がらないでしょ，といったような理由で，いきなり偏微分の話からかましていくスタイルで，三町氏のテキストの出だしと同じである。

道草ついでにいうと，偏微分の計算は 1 変数関数の微分そのものだから，そこはスムーズに接続できるとしても，全微分という，1 変数関数の微分概念の多変数関数版の正統後継者と考えられる「線形写像による 1 次近似」へと話を進めるのはどうやるのであろうか。実はそもそも 1 変数関数のグラフの接線が何故接線と呼ばれる代物であるのかといったことは高校の「数学 III」でもスルーされるような，観念的なお話であるので，その辺の話をゴチャゴチャやって，しかも多変数の線形（もしくは比例）関数とはなんぞや，といった話も一席ぶつとなると，途端に内容の難易度が跳ね上がる。そのため，全微分なるものをバッサリ大学初年級の微分積分の課程から放逐するのも一つの手なのかもしれない。さすがに私はそこまで思い切った簡略化を推し進める勇気は今のところないが，今後の可能性の一つとして真剣に検討すべき選択肢の一つであるような気がしてならない。

とにもかくにも，4 月になってしまったので間もなく新学期が始まる。

20 年教え続けてきたが，今年度も私が教える内容は「数 IV」には手が届かず，その半歩手前の「数 IIIS」に留まる予定である。

III と IV の中間，つまり 3.5 に相当する数字をローマ数字で表せるのか気になってググってみたら，ローマ数字に関する Wikipedia の日本語版でまず小数表示が存在することを知り，より詳しい内容については英語版 (Roman_numerals#Fractions) を参照した。それによるとローマ数字の流儀では分数はなぜか 12 進法になるそうだが，1/2，つまり 6/12 は half を意味する semis の頭文字を取って S と表すそうだ。

そういえば，私の専門は非線型偏微分方程式論ということになっているが，非線形性があまり強くない場合は古くは semi-linear，現在では semilinear と英語で綴られ，「半線型」という訳語が充てられている。また，発展方程式と呼ばれるタイプの場合，半群的な取り扱いというものが用いられることがあるが，「半群」は semigroup である。代数方面では「半単純」 semisimple という用語を見かけたこともある。解析学では「半連続」 semicontinuous というのがあったのも思い出した。

球面を赤道で切った半分も仲間かなと思ったのだが，それは hemisphere という。訳語は「半球面」であるが，semi ではなくて hemi である。

hemi の方はギリシャ語由来で，それがラテン語版になると semi に変化するそうで，両者は無関係なわけではないらしい。

気になったのでもうちょい調べたら，demi というのも出てきた。ギリシャ神話でおなじみの半神は英語だと demigod になる。ファンタジー系のマンガなどで亜人なるものが出てくることがあるが，それをデミヒューマン (demihuman，半人) なんて呼んだりしているな。

それはともかく，semi- という接頭辞が「半分」を意味しているらしいことは私にとってはかなりなじみ深かったはずなのだが，今の今まですっかり忘れていた。そうかー，semis が語源なのねー。



ということで，数 III と数 IV の間に位置する，極めて中途半端な内容の「微分積分学」の講義は「数 IIIS 方式」と称することを提案したい。これが本記事の主旨である。