虚数
2009年09月23日 | 数
虚数は、字面のように はたして虚（むな）しい数なのだろうか ❔
あるいは、
「アイ」に充ちた面をも持ち合わせていようか ❔
負の数と虚数はよく似ている。
１ を加えると ０ になる数を１ の「 負の数」と呼び、「－１」と書き、
２乗すると 「－１」 になる数を「虚数」と呼び、「 i 」と書く 。
なるほど、読み方とおり「アイ」そのものだった。
いままで、
Ｘ2＋１＝０
から、Ｘの値を求め、
Ｘ＝±√‐1 を導き、
こんな解は、ないよりあったとした方が何かと便利ということらしい。
例えば、
電気回路の計算にすばらしい威力を示し、複素数なしの計算などは考えられないという。
平面の二次元から、虚数を交えた立体の3次元空間を構成する。
つまり、虚数は 実数とは別の方向に数の概念を拡張した。
虚数とは、鏡に映る虚像のような存在なのだろう。
ないはずの像が見える。それを数値化したのを虚数と考えればよいのだろうか。
あるいは、
「アイ」に充ちた面をも持ち合わせていようか ❔負の数と虚数はよく似ている。
１ を加えると ０ になる数を１ の「 負の数」と呼び、「－１」と書き、
２乗すると 「－１」 になる数を「虚数」と呼び、「 i 」と書く 。
なるほど、読み方とおり「アイ」そのものだった。
いままで、
Ｘ2＋１＝０
から、Ｘの値を求め、
Ｘ＝±√‐1 を導き、
こんな解は、ないよりあったとした方が何かと便利ということらしい。
例えば、
電気回路の計算にすばらしい威力を示し、複素数なしの計算などは考えられないという。
平面の二次元から、虚数を交えた立体の3次元空間を構成する。
つまり、虚数は 実数とは別の方向に数の概念を拡張した。
虚数とは、鏡に映る虚像のような存在なのだろう。
ないはずの像が見える。それを数値化したのを虚数と考えればよいのだろうか。
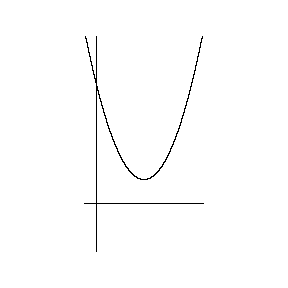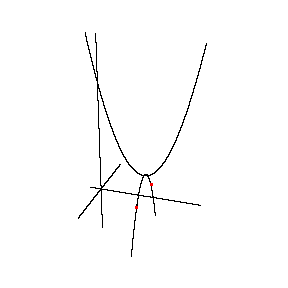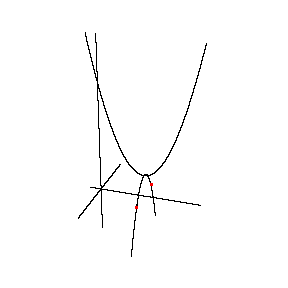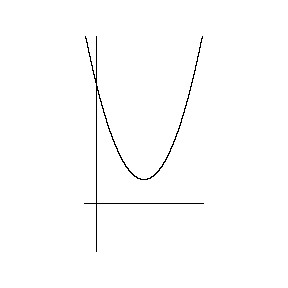
| 虚数を、次のように目に見えるグラフで説明すると、 ①まず、はじめに次の２次方程式をグラフにする。χ軸との交点が、χの解１と３。  ②虚数解のとき、 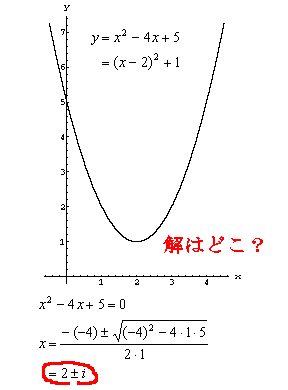 χ 軸 y 軸に垂直に虚軸を導入。 すると見えていた放物線に、 見えなかった下半分が表れる。 χ の解は、 赤い点 ２±ｉ |
アクセス
トータル
ランキング
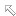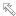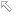
そんな風に思えば、のしてんさんの詩の如く、心の波長にあうと見えぬものが見えたりしそうです。
そうです。
「虚数」は見えないものを数値化することにより、ないよりあったとした方が何かと便利だとされているようです。
２乗すると 「－１」 になる数を「虚数」と呼び、「 i 」と書く 。
－１は小学校から教えられて疑問も持たなかったのですが虚数には苦労しました。
けれど、－１も虚数と同じ位置にあることをあらためて教えられました。
実在しない（見えないもの）を見えるようにする。人間の空想の力ですね。
しかも空想は何もないのではないということ。ただ見えないだけで、実在しているということがあらためて感動を呼びおこします。
ありがとうございました。
陸奥を「六」と語呂合わせしたＨＰをご覧ください。
http://iinad55.at.infoseek.co.jp/6.html
こんど１０月に東北に連れて行ってもらいますので、参考にいたします。
＞最後の４行は理解できませんでしたね。
虚数を グラフにしてみましたから、もういちどオコシください。
ippuさんは、数学がお得意なのですね。
(鷲谷芝嵐)さん へ
「にいがた」総おどりは、長い祭ですね。
「にぎやか」です。
祭は「虚勢」を張るわけではありませんね。
(銭無のとっつあん) へ
魏の曹操と卑弥呼がからむ小説を読んだことがありますよ。
泉涌寺の門のあたりに、楊貴妃が祀られていましたネ。
虚数も、考えようによっては「神」の存在みたいです。
信じる方には怒られそうですが、神はないとするより あるとした方が
何事をもすんなりさせてしまうような魔力があります。
http://blog.goo.ne.jp/iinna/e/0c34a1319fcb3a86165a525a9b4a463c
社会科学は、相対的な理論で構成しますが、自然科学は、絶対的な理論…。
名前は虚数でも絶対的な解答があるのですね。
今更、首を突っ込みたくないです。
でも≪本文を読む≫をクリックし全文を表示させたら正しく表示されていたので納得しました。
何十年も前に習った虚数をまだ理解していました。まだ大丈夫です。
でも、最後の４行は理解できませんでしたね。