こんにちは。東久留米市の学習塾塾長です。
涼しい北よりの風が吹いていて過ごしやすい日になりました。午後には、この風が運んできた湿った空気のために雨が降るようです。涼しい夜になりそうです。
さて、今回は2013年ジュニア数学オリンピック予選に出題された整数問題を取り上げます。
問題は、
「201/a+3/bが整数であるような正の整数の組(a,b)はいくつあるか。」
です。
早速、取り掛かりましょう。
ここは定石通り、aとbの最大公約数をgとして、
a=mg (1)
b=ng (2)
mとnは互いに素である正の整数
とおくのがよいでしょう。
そこで(1)(2)を与式に代入して、
201/(mg)+3/(ng)=1/g(201/m+3/n)
=1/g((201n+3m)/(mn)) (3)
を得ます。
このとき、(3)は整数なので、mは201n+3mの約数で、したがって、mは201nの約数になります。
ところが、mとnは互いに素であるので、mは201の約数で、すなわち、
m=1、3、67、201 (4)
のいずれかになります。
同様に、nは201n+3mの約数であることから、nは3mの約数で、したがって3の約数です。
つまり、
n=1、3
のいずれかになります。
以上から、mとnの組合せ[m,n]は、mとnが互いに素でない[3,3][207,3]を除くと、
[1,1][1,3][3,1][67,1][67,3][201,1]
になります。
続いて、これらの各[m,n]について、有り得るgの個数を計算しましょう。すると(1)(2)から、このgの個数が(a,b)の組合せの個数になります。
・[1,1]のとき
(3)=1/g(201+3)=1/g・204
になり、これが整数になるので、gは204の約数です。
ところが、
204=2^2×3×17
と素因数分解されるので、204の約数の個数は、(2+1)(1+1)(1+1)=3×2×2=12個で、(a,b)の個数は12個です。
(ここで、ある正の整数Nが、

と素因数分解されるとき、Nの約数の個数は、
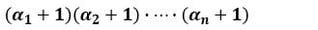
になります。約数と式の展開)
・[1,3]のとき
(3)=1/g((201・3+3)/3)=g/1・202
になり、gは202の約数です。
ここで、
202=2×101
から、202の約数の個数は、(1+1)(1+1)=4個で、(a,b)の個数は4個です。
・[3,1]のとき
(3)=1/g((201・1+3・3)/3)=1/g・70
になり、gは70の約数です。
ここで、
70=2×5×7
から、202の約数の個数は、(1+1)(1+1)(1+1)=8個で、(a,b)の個数は8個です。
・[67,1]のとき
(3)=1/g((201+3・67)/67=1/g・6
になり、gは6の約数です。
ここで、
6=2×3
から、6の約数の個数は、(1+1)(1+1)=4個で、(a,b)の個数は4個です。
・[67,3]のとき(3)=1/g((201・3+3・67)/(67・3))=1/g・4
になり、gは4の約数です。
ここで、
4=2^2
から、4の約数は、2+1=3個で、(a,b)の個数は3個です。
・[201,1]のとき
(3)=1/g((201+3・201)/201)=1/g・4
になり、gは4の約数です。
ここで、
4=2^2
から、4の約数は、2+1=3個で、(a,b)の個数は3個です。
以上から、(a,b)の組合せの個数は、12+4+8+4+3+3=34個で、これが答えです。
頻出の解法パターンなので、頭に入れておくと役に立つでしょう。
涼しい北よりの風が吹いていて過ごしやすい日になりました。午後には、この風が運んできた湿った空気のために雨が降るようです。涼しい夜になりそうです。
さて、今回は2013年ジュニア数学オリンピック予選に出題された整数問題を取り上げます。
問題は、
「201/a+3/bが整数であるような正の整数の組(a,b)はいくつあるか。」
です。
早速、取り掛かりましょう。
ここは定石通り、aとbの最大公約数をgとして、
a=mg (1)
b=ng (2)
mとnは互いに素である正の整数
とおくのがよいでしょう。
そこで(1)(2)を与式に代入して、
201/(mg)+3/(ng)=1/g(201/m+3/n)
=1/g((201n+3m)/(mn)) (3)
を得ます。
このとき、(3)は整数なので、mは201n+3mの約数で、したがって、mは201nの約数になります。
ところが、mとnは互いに素であるので、mは201の約数で、すなわち、
m=1、3、67、201 (4)
のいずれかになります。
同様に、nは201n+3mの約数であることから、nは3mの約数で、したがって3の約数です。
つまり、
n=1、3
のいずれかになります。
以上から、mとnの組合せ[m,n]は、mとnが互いに素でない[3,3][207,3]を除くと、
[1,1][1,3][3,1][67,1][67,3][201,1]
になります。
続いて、これらの各[m,n]について、有り得るgの個数を計算しましょう。すると(1)(2)から、このgの個数が(a,b)の組合せの個数になります。
・[1,1]のとき
(3)=1/g(201+3)=1/g・204
になり、これが整数になるので、gは204の約数です。
ところが、
204=2^2×3×17
と素因数分解されるので、204の約数の個数は、(2+1)(1+1)(1+1)=3×2×2=12個で、(a,b)の個数は12個です。
(ここで、ある正の整数Nが、

と素因数分解されるとき、Nの約数の個数は、
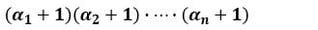
になります。約数と式の展開)
・[1,3]のとき
(3)=1/g((201・3+3)/3)=g/1・202
になり、gは202の約数です。
ここで、
202=2×101
から、202の約数の個数は、(1+1)(1+1)=4個で、(a,b)の個数は4個です。
・[3,1]のとき
(3)=1/g((201・1+3・3)/3)=1/g・70
になり、gは70の約数です。
ここで、
70=2×5×7
から、202の約数の個数は、(1+1)(1+1)(1+1)=8個で、(a,b)の個数は8個です。
・[67,1]のとき
(3)=1/g((201+3・67)/67=1/g・6
になり、gは6の約数です。
ここで、
6=2×3
から、6の約数の個数は、(1+1)(1+1)=4個で、(a,b)の個数は4個です。
・[67,3]のとき(3)=1/g((201・3+3・67)/(67・3))=1/g・4
になり、gは4の約数です。
ここで、
4=2^2
から、4の約数は、2+1=3個で、(a,b)の個数は3個です。
・[201,1]のとき
(3)=1/g((201+3・201)/201)=1/g・4
になり、gは4の約数です。
ここで、
4=2^2
から、4の約数は、2+1=3個で、(a,b)の個数は3個です。
以上から、(a,b)の組合せの個数は、12+4+8+4+3+3=34個で、これが答えです。
頻出の解法パターンなので、頭に入れておくと役に立つでしょう。