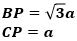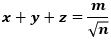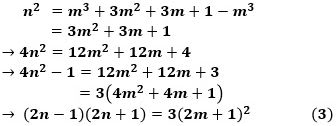こんにちは。東久留米市の学習塾塾長です。
今回は、2006年AIMEの図形問題です。
問題は、
「∠A<45°、∠C=90°、AB=4の△ABCにおいて、辺AB上に、
∠APC=2∠ACP、CP=1
になる点Pをとる。
ここで、

が

と表せるとき、p+q+rの値を求めよ。ただし、p、q、rは正の整数で、rは素数の平方数で割り切れないものとする。」
です。
図1に問題の図を描きました。

▲図1.問題の図を描きました
図1を眺めると、直角と、中心角と円周角を想起させる倍角が目に付くので、図2のように、△ABCの外接円ωを描いてみましょう。このとき、ωの中心Oは辺ABの中点になります。

▲図2.△ABCの外接円ωを描きました
ここで直線CPとωとの交点で、Cでない方をQとし、さらにOとQを結ぶと、∠AOQと∠ACQは中心角と円周角になるので、
∠AOQ=2∠ACQ=2●
です。
すると、
∠QPO=∠QPC-∠APC=180°-2●
∠QOP=∠AOB-∠AOQ=180°-2●
から、△QPOは二等辺三角形になり、このとき線分OQはωの半径なので、PQ=OQ=2です。
あとは図3のように、Oから直線CQに下した垂線の足をHとして、直角三角形OQHとOPHに三平方の定理を適用して必要な線分の長さを求めればお仕舞です。

▲図3.Oから直線CQに下した垂線の足をHとしました
まず直角三角形OQHに三平方の定理を適用すると、

が成り立ち、これに、

を代入して整理すると、

です。
続いて直角三角形OPHに三平方の定理を適用すると、

が成り立ち、これに

を代入して整理すると、

です。
すると、

になり、これらから

です。
したがって、p=3、q=2、r=2からp+q+r=3+2+2= 7 で、これが答えです。
簡単な問題です。
今回は、2006年AIMEの図形問題です。
問題は、
「∠A<45°、∠C=90°、AB=4の△ABCにおいて、辺AB上に、
∠APC=2∠ACP、CP=1
になる点Pをとる。
ここで、

が

と表せるとき、p+q+rの値を求めよ。ただし、p、q、rは正の整数で、rは素数の平方数で割り切れないものとする。」
です。
図1に問題の図を描きました。

▲図1.問題の図を描きました
図1を眺めると、直角と、中心角と円周角を想起させる倍角が目に付くので、図2のように、△ABCの外接円ωを描いてみましょう。このとき、ωの中心Oは辺ABの中点になります。

▲図2.△ABCの外接円ωを描きました
ここで直線CPとωとの交点で、Cでない方をQとし、さらにOとQを結ぶと、∠AOQと∠ACQは中心角と円周角になるので、
∠AOQ=2∠ACQ=2●
です。
すると、
∠QPO=∠QPC-∠APC=180°-2●
∠QOP=∠AOB-∠AOQ=180°-2●
から、△QPOは二等辺三角形になり、このとき線分OQはωの半径なので、PQ=OQ=2です。
あとは図3のように、Oから直線CQに下した垂線の足をHとして、直角三角形OQHとOPHに三平方の定理を適用して必要な線分の長さを求めればお仕舞です。

▲図3.Oから直線CQに下した垂線の足をHとしました
まず直角三角形OQHに三平方の定理を適用すると、

が成り立ち、これに、

を代入して整理すると、

です。
続いて直角三角形OPHに三平方の定理を適用すると、

が成り立ち、これに

を代入して整理すると、

です。
すると、

になり、これらから

です。
したがって、p=3、q=2、r=2からp+q+r=3+2+2= 7 で、これが答えです。
簡単な問題です。