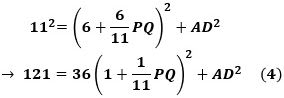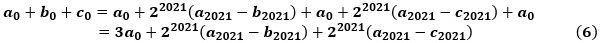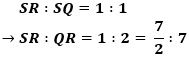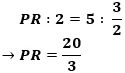こんにちは。東久留米市の学習塾塾長です。
今回は、2021年日本数学オリンピック予選の問題で、これが最後の記事になります。
問題は、
「三角形ABCの辺AB、AC上にそれぞれ点D、Eがあり、4点D、B、C、Eは同一円周上にある。また、四角形DBCEの内部に点Pがあり、
∠BDP=∠BPC=∠PECをみたしている。
AB=9、AC=11、DP=1、EP=3のとき、
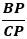
の値を求めよ。
ただし、XYで線分XYの長さを表すものとする。」
です。
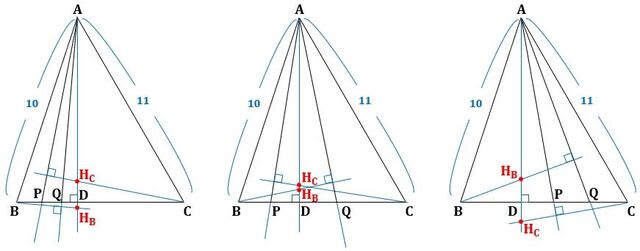
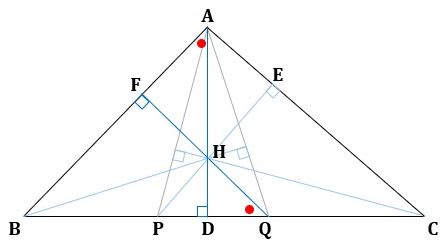
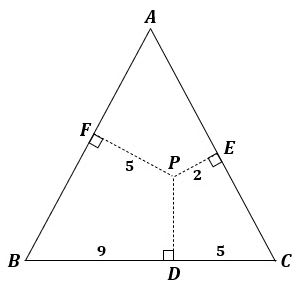
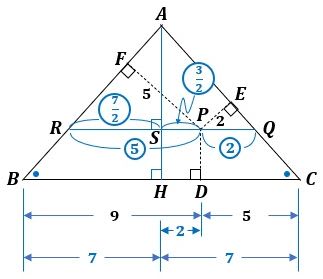
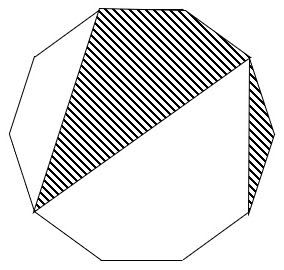
図1に問題の図を描きました。
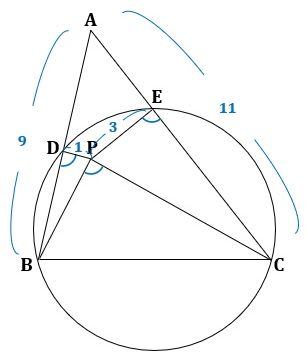
▲図1.問題の図を描きました
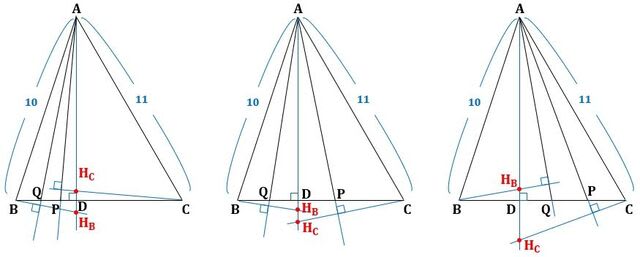
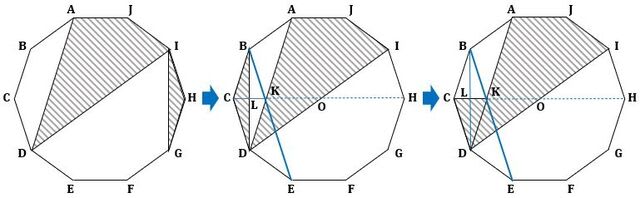
図2のように、直線DPと直線ACの交点をQ、四角形DBCEの外接円の交点でDでない方をSとし、直線EPと直線ABの交点をR、四角形DBCEの外接円の交点でEでない方をTとすると、仮定と円周角の定理から、
∠BDS=∠BPC>∠BDC
→ 弧BS>弧BC
になり、SはBがない方の弧CE上の点で、したがって、Qは線分CE上にあります。
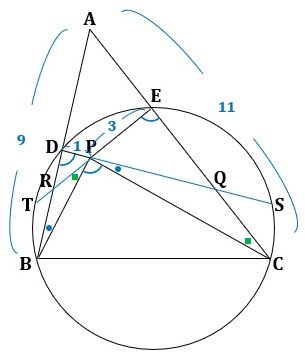
▲図2.Qは線分CE上の点で、Rは線分BD上の点です
同様に、
∠CET=∠CPB>∠CEB
→ 弧CT>弧BC
になり、TはCがない方の弧BT上の点で、したがって、Rは線分BD上にあります。
そこで、△BDPに注目すると、三角形の2つの内角と外角の関係から、
∠BPQ=∠DBP+∠BDP
が成り立ち、このとき、
∠BPQ=∠CPQ+∠BPC=∠CPQ+∠BDP
から
∠DBP=∠CPQ
で、一方、△CEPに注目すると、
∠CPR=∠ECQ+∠CEP
が成り立ち、このとき、
∠CPR=∠BPR+∠BPC=∠BPR+∠CEP
から
∠ECQ=∠BPR
になり、したがって、△BPR∽△PCQです。
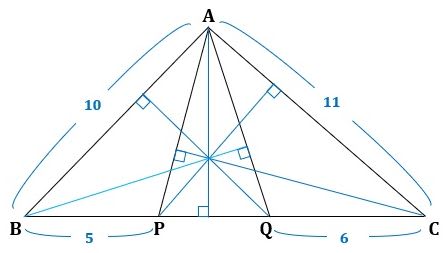
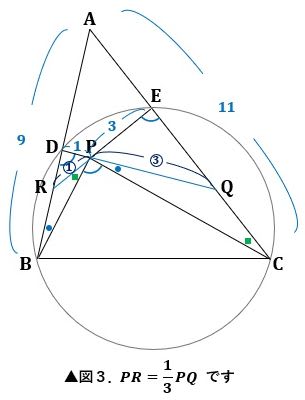
また図3のように、∠PDR=∠PEQ(仮定)、∠DPR=∠EPQ(対頂角)から
△DPR∽△EPQ
になり、このとき、DP=1、EP=3から

です。
ここで、四角形DBCEの外接円と線分AB、ACに方べきの定理を適用すると、
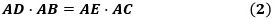
が成り立ちます。
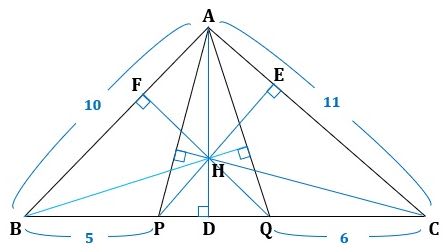
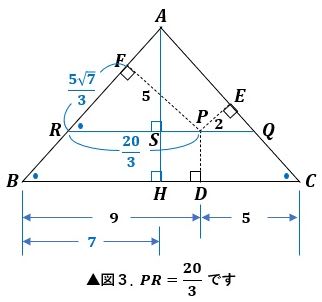
また、∠QDR=∠QERで、このとき円周角の定理の逆から、図4のように、D、R、Q、Eは同一円周上にあり、この円と線分AR、AQに方べきの定理を適用すると、
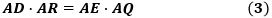
が成り立ちます。

▲図4.AD・AR=AE・AQです
そこで、(3)を(2)で除して整理すると、
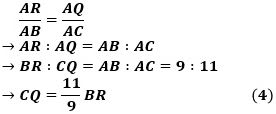
です。
このとき△BPR∽△PCQから、

が成り立ち、ここで、右側の等式に(1)と(4)を代入して整理すると、

になり、これと(5)の左側の等式から、

で、これが答えです。
このブログを始めてから8年になります。ご覧くださった皆様に感謝します。ありがとうございました。
今回は、2021年日本数学オリンピック予選の問題で、これが最後の記事になります。
問題は、
「三角形ABCの辺AB、AC上にそれぞれ点D、Eがあり、4点D、B、C、Eは同一円周上にある。また、四角形DBCEの内部に点Pがあり、
∠BDP=∠BPC=∠PECをみたしている。
AB=9、AC=11、DP=1、EP=3のとき、
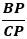
の値を求めよ。
ただし、XYで線分XYの長さを表すものとする。」
です。
図1に問題の図を描きました。

▲図1.問題の図を描きました
図2のように、直線DPと直線ACの交点をQ、四角形DBCEの外接円の交点でDでない方をSとし、直線EPと直線ABの交点をR、四角形DBCEの外接円の交点でEでない方をTとすると、仮定と円周角の定理から、
∠BDS=∠BPC>∠BDC
→ 弧BS>弧BC
になり、SはBがない方の弧CE上の点で、したがって、Qは線分CE上にあります。

▲図2.Qは線分CE上の点で、Rは線分BD上の点です
同様に、
∠CET=∠CPB>∠CEB
→ 弧CT>弧BC
になり、TはCがない方の弧BT上の点で、したがって、Rは線分BD上にあります。
そこで、△BDPに注目すると、三角形の2つの内角と外角の関係から、
∠BPQ=∠DBP+∠BDP
が成り立ち、このとき、
∠BPQ=∠CPQ+∠BPC=∠CPQ+∠BDP
から
∠DBP=∠CPQ
で、一方、△CEPに注目すると、
∠CPR=∠ECQ+∠CEP
が成り立ち、このとき、
∠CPR=∠BPR+∠BPC=∠BPR+∠CEP
から
∠ECQ=∠BPR
になり、したがって、△BPR∽△PCQです。
また図3のように、∠PDR=∠PEQ(仮定)、∠DPR=∠EPQ(対頂角)から
△DPR∽△EPQ
になり、このとき、DP=1、EP=3から

です。

ここで、四角形DBCEの外接円と線分AB、ACに方べきの定理を適用すると、
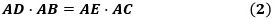
が成り立ちます。
また、∠QDR=∠QERで、このとき円周角の定理の逆から、図4のように、D、R、Q、Eは同一円周上にあり、この円と線分AR、AQに方べきの定理を適用すると、
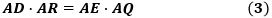
が成り立ちます。

▲図4.AD・AR=AE・AQです
そこで、(3)を(2)で除して整理すると、
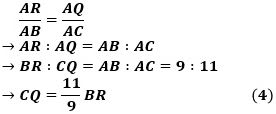
です。
このとき△BPR∽△PCQから、

が成り立ち、ここで、右側の等式に(1)と(4)を代入して整理すると、

になり、これと(5)の左側の等式から、

で、これが答えです。
このブログを始めてから8年になります。ご覧くださった皆様に感謝します。ありがとうございました。