こんにちは。東久留米市の学習塾塾長です。
晴れ模様ですが風が少し強く吹いています。梅雨前線は東北地方の北側にあるので台風が過ぎれば梅雨明けですね。
中3数学の期末試験で因数分解の問題が出題された思いますが、それらのすべてが2次の多項式が与えられ、それを因数分解するというものだったと思います。
例えば、
x^2+6x+5 式(1) (x^2 はxの2乗を表します)
とあれば、(x+1)(x+5)と解答して○が貰えるといった具合です。
しかし、ここで与式が
x^2+6x+2 式(2)
とすると、整数係数の範囲では因数分解できません。このようにあるn次多項式が因数分解できないことを証明するときに使うのが、「アイゼンシュタインの定理」です。
それは、「整数係数を持つ 有理数体上の多項式
f(x)=a0+a1x^1+a2x^2+・・・+anx^n
に対しある素数 p が存在し、p が係数 a0、a1、a2、・・・、a(n-1) を割り、 anを割らず、かつ p^2 が a0 を割らないとき、f(x) は既約である」というもので、これを使い勝手の良いように言い直すと、
(1)a0 は、素数pの倍数だが、p^2の倍数ではない
(2)a1、a2、・・・、a(n-1) はpの倍数
(3)an は、pの倍数ではない
これらの3つの条件を満たす式は既約、つまり因数分解できないということです。
そこで、式(1)(2)のようにxの2次項の係数が1、xの項の係数が6で定数項を1から10までの整数とした2次式で確認してみましょう。(実際に因数分解したり、解の公式や判別式が平方数になるかを調べれば簡単に既約や可約か判りますが・・・)
例えば、x^2+6x+1 では、定数項1を倍数とする素数がないので、残念ながら判定不可となります。
次に、x^2+6x+2 は、定数項2を倍数とする素数2があり、また定数項2は、素数2の2乗の4の倍数でないので、条件(1)はOKです。条件(2)は、xの項の係数6は2の倍数なので、これもOKです。条件(3)は、x^2 の項の係数1は2の倍数でないのでOKです。以上より条件(1)(2)(3)を満たすので、x^2+6x+2 は既約(因数分解できない)となります。
これらの結果を表にまとめます。
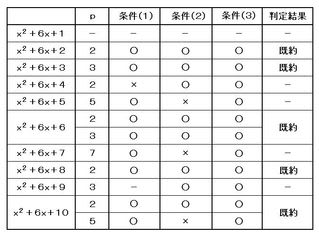
▲表.x^2+6x+A (A=1,2,・・・,10)を調べた結果
この表に示すように、調べた10式に対して、x^2+6x+2、x^2+6x+3、x^2+6x+6、x^2+6x+8 および、x^2+6x+10 の5つが既約と判ります。
残りの5式については、x^2+6x+1、x^2+6x+4 および、x^2+6x+7 の3式は既約(ここで、x^2+6x+4については、xをx+2とするとp=5のとき、また、x^2+6x+7 については、xをx+1、とするとp=2のとき、条件(1)(2)(3)を満たすことが判ります)、x^2+6x+5=(x+1)(x+5) 、x^2+6x+9=(x+3)^2 となり可約となります。
このように「アイゼンシュタインの定理」は、式が既約である十分条件を与えるもので条件(1)(2)(3)のどれかを満たさない場合、その式が可約とはならないことに注意してください。
今回は簡単な2次式で説明しましたが、次回は高次式に適用してみます。
晴れ模様ですが風が少し強く吹いています。梅雨前線は東北地方の北側にあるので台風が過ぎれば梅雨明けですね。
中3数学の期末試験で因数分解の問題が出題された思いますが、それらのすべてが2次の多項式が与えられ、それを因数分解するというものだったと思います。
例えば、
x^2+6x+5 式(1) (x^2 はxの2乗を表します)
とあれば、(x+1)(x+5)と解答して○が貰えるといった具合です。
しかし、ここで与式が
x^2+6x+2 式(2)
とすると、整数係数の範囲では因数分解できません。このようにあるn次多項式が因数分解できないことを証明するときに使うのが、「アイゼンシュタインの定理」です。
それは、「整数係数を持つ 有理数体上の多項式
f(x)=a0+a1x^1+a2x^2+・・・+anx^n
に対しある素数 p が存在し、p が係数 a0、a1、a2、・・・、a(n-1) を割り、 anを割らず、かつ p^2 が a0 を割らないとき、f(x) は既約である」というもので、これを使い勝手の良いように言い直すと、
(1)a0 は、素数pの倍数だが、p^2の倍数ではない
(2)a1、a2、・・・、a(n-1) はpの倍数
(3)an は、pの倍数ではない
これらの3つの条件を満たす式は既約、つまり因数分解できないということです。
そこで、式(1)(2)のようにxの2次項の係数が1、xの項の係数が6で定数項を1から10までの整数とした2次式で確認してみましょう。(実際に因数分解したり、解の公式や判別式が平方数になるかを調べれば簡単に既約や可約か判りますが・・・)
例えば、x^2+6x+1 では、定数項1を倍数とする素数がないので、残念ながら判定不可となります。
次に、x^2+6x+2 は、定数項2を倍数とする素数2があり、また定数項2は、素数2の2乗の4の倍数でないので、条件(1)はOKです。条件(2)は、xの項の係数6は2の倍数なので、これもOKです。条件(3)は、x^2 の項の係数1は2の倍数でないのでOKです。以上より条件(1)(2)(3)を満たすので、x^2+6x+2 は既約(因数分解できない)となります。
これらの結果を表にまとめます。

▲表.x^2+6x+A (A=1,2,・・・,10)を調べた結果
この表に示すように、調べた10式に対して、x^2+6x+2、x^2+6x+3、x^2+6x+6、x^2+6x+8 および、x^2+6x+10 の5つが既約と判ります。
残りの5式については、x^2+6x+1、x^2+6x+4 および、x^2+6x+7 の3式は既約(ここで、x^2+6x+4については、xをx+2とするとp=5のとき、また、x^2+6x+7 については、xをx+1、とするとp=2のとき、条件(1)(2)(3)を満たすことが判ります)、x^2+6x+5=(x+1)(x+5) 、x^2+6x+9=(x+3)^2 となり可約となります。
このように「アイゼンシュタインの定理」は、式が既約である十分条件を与えるもので条件(1)(2)(3)のどれかを満たさない場合、その式が可約とはならないことに注意してください。
今回は簡単な2次式で説明しましたが、次回は高次式に適用してみます。




















