こんにちは。東久留米市の学習塾塾長です。
昨日の強風が治まって過ごしやすい日になりました。しばらくの間、高気圧に覆われ暖かい晴れの日が続くようです。
さて、今回は平成28年度都立高校数学入試問題を取り上げます。
問題は、日比谷高など都立御三家で出題された大問2の2次関数グラフ問題で、それは、
「下の図1で、点Oは原点、曲線fは関数y=1/4・x^2 のグラフ、曲線gは関数y=ax^2 (a>1/4)のグラフを表している。
点A、点Bはともに曲線f上にあり、点Aのx座標はt (0<t<6)、点Bのx座標は t-6 である。
点Cは曲線g上にあり、x座標は負の数である。
点Oと点A、点Oと点B、点Aと点C、点Bと点Cをそれぞれ結ぶ。
次の各問に答えよ。

▲図1.問題図(1)
[問1]a=5/4のとき、次の(1)、(2)に答えよ。
(1)t=4、点Cのx座標が-2のとき、2点A、Cを通る直線の式を求めよ。
(2)四角形OABCが平行四辺形となるとき、tの値を求めよ。
ただし、答えだけではなく、答えを求める過程が分かるように、途中の式や計算なども書け。
[問2]下の図2は、図1において、t=3、点Cのx座標が-3/2のとき、点Oと点Cを結んだ場合を表している。
△OACの面積と△OCBの面積の比が2:1のとき、aの値を求めよ。」

▲図2.問題図(2)
です。
まず図3のように、本問全体に共通する条件を書き入れましょう。

▲図3.本問全体に共通する条件を書き入れました
それでは、[問1]の(1)に取り掛かりましょう。
ここで図4のように、[問1]の(1)に与えられた条件を書き入れます。

▲図4.[問1]の(1)に与えられた条件を書き入れました
t=4なので、点Aのx座標は4、点Aがy=1/4・x^2上にあるので、そのy座標は4、つまり、点A(4,4)になります。
一方、点Cのx座標は-2、点Cがy=5/4・x^2上にあるので、そのy座標は5、つまり、点C(-2,5)になります。
ここで、2点A、Cを通る直線をy=px+qとすると、p=(4-5)/(4-(-2))=-1/6で、
y=-1/6・x+q
になります。
また、この直線は点Aを通るので、
4=-1/6・4+q
q=4+2/3
=14/3
になり、求める直線の式は、
y=-1/6・x+14/3
で、これが答えです。
次の[問1]の(2)です。
点AとBのx座標はそれぞれtとt-6で、これらの点はy=1/4・x^2上にあるので、それらのy座標はそれぞれ1/4・t^2、1/4・(t-6)^2です。
つまり、点AとBの座標は、それぞれ、
点A(t,1/4・t^2)
点B(t-6,1/4・(t-6)^2)
です。
次に点Cの座標を求めます。
与えられた条件から、四角形OABCは平行四辺形なので、
OA=BC
OA//BC
が成り立ち、OAのx変化量がBCのx変化量に等しいので、点Cのx座標は2t-6で、また、点Cはy=5/4・x^2上にあるので、そのy座標は、5/4・(2t-6)^2です。
つまり、点Cの座標は、
点C(2t-6,5/4・(2t-6)^2)
です。
ここで、点A、点B、点Cの座標を図5に書き入れましょう。
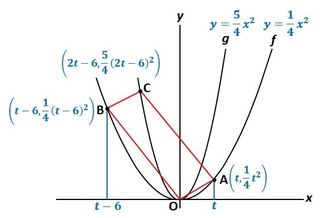
▲図5.点A、点B、点Cの座標を書き入れました
あとは、これらの座標から四角形OABCが平行四辺形になる条件を立式すればOKです。
そこで、点Cのx座標を求めるときOA=BCを使ったので、OA//OB、つまり、直線OAと直線BCの傾きが等しくなる条件を立式するのが簡単でしょう。(最後に記したように、平行四辺形になるための5つの条件のどれを使ってもOKです)
そこで、それぞれの直線の傾きを求めて等式をつくると、
 [1]
[1]
になります。
そして、これを整理して因数分解すると、
 [2]
[2]
です。
[2]から、t=2または4ですが、それぞれの場合の点Cのx座標を計算すると、
t=2のとき、2×2-6=-2
t=4のとき、2×4-6=2
となり、点Cのx座標が負の数であることから、t=2で、これが答えです。
続いて[問2]です。
まず、与えられた条件で、点A、点B、点Cの座標を計算し、図6に書き入れましょう。

▲図6.点A、点B、点Cの座標を書き入れました
このとき、直線OCの式は、
 [3]
[3]
です。
また図6に示すように、点Aと点Bを結んだ直線と、点Oと点Cを結んだ直線との交点をM、点Aから直線OCに下ろした垂線の足をN、点Bから直線OCに下ろした垂線の足をLとします。
すると、△OACの面積S(A)と△OCBの面積S(B)は、それぞれ、
S(A)=OC×AN×1/2
S(B)=OC×BL×1/2
になり、その面積比は、
S(A):S(B)=OC×AN×1/2:OC×BL×1/2
=AN:BL
です。
また、与えられた条件からこの面積比が2:1になので、
AN:BL=2:1
になります。
一方、△ANM∽△BLMから、
AN:BL=AM:BM
なので、
AM:BM=2:1
です。
ここで、点Aと点Bのy座標はどちらも9/4で、点Mは直線AB上にあるので、点Mのy座標は9/4です。
さらに、線分ABの長さは6で、点Mは線分ABを2:1に内分するので、点Mのx座標は-1です。
つまり、点Mの座標は(-1,9/4)になります。
そして、点Mは直線OC上にあるので、[3]に(-1,9/4)を代入すると、
9/4=-3/2・a・(-1)
a=3/2
で、これが答えです。
[問1]の(2)は、平行四辺形になるための5つの条件
・2組の対辺がそれぞれ平行
・2組の対辺がそれぞれ等しい
・2組の対角がそれぞれ等しい
・対角線がそれぞれの中点で交わる
・1組の対辺が平行で長さが等しい
のどれを使ってもOKです。(ここでは、最後の「1組の対辺が平行で長さが等しい」を使いました)
また、[問2]は、点(x1,y1)から直線ax+by+c=0に下ろした垂線の長さがlax1+by1+cl/√(a^2+b^2)になることを利用する方法もあります。
興味のある人は調べてみてください。
昨日の強風が治まって過ごしやすい日になりました。しばらくの間、高気圧に覆われ暖かい晴れの日が続くようです。
さて、今回は平成28年度都立高校数学入試問題を取り上げます。
問題は、日比谷高など都立御三家で出題された大問2の2次関数グラフ問題で、それは、
「下の図1で、点Oは原点、曲線fは関数y=1/4・x^2 のグラフ、曲線gは関数y=ax^2 (a>1/4)のグラフを表している。
点A、点Bはともに曲線f上にあり、点Aのx座標はt (0<t<6)、点Bのx座標は t-6 である。
点Cは曲線g上にあり、x座標は負の数である。
点Oと点A、点Oと点B、点Aと点C、点Bと点Cをそれぞれ結ぶ。
次の各問に答えよ。

▲図1.問題図(1)
[問1]a=5/4のとき、次の(1)、(2)に答えよ。
(1)t=4、点Cのx座標が-2のとき、2点A、Cを通る直線の式を求めよ。
(2)四角形OABCが平行四辺形となるとき、tの値を求めよ。
ただし、答えだけではなく、答えを求める過程が分かるように、途中の式や計算なども書け。
[問2]下の図2は、図1において、t=3、点Cのx座標が-3/2のとき、点Oと点Cを結んだ場合を表している。
△OACの面積と△OCBの面積の比が2:1のとき、aの値を求めよ。」

▲図2.問題図(2)
です。
まず図3のように、本問全体に共通する条件を書き入れましょう。

▲図3.本問全体に共通する条件を書き入れました
それでは、[問1]の(1)に取り掛かりましょう。
ここで図4のように、[問1]の(1)に与えられた条件を書き入れます。

▲図4.[問1]の(1)に与えられた条件を書き入れました
t=4なので、点Aのx座標は4、点Aがy=1/4・x^2上にあるので、そのy座標は4、つまり、点A(4,4)になります。
一方、点Cのx座標は-2、点Cがy=5/4・x^2上にあるので、そのy座標は5、つまり、点C(-2,5)になります。
ここで、2点A、Cを通る直線をy=px+qとすると、p=(4-5)/(4-(-2))=-1/6で、
y=-1/6・x+q
になります。
また、この直線は点Aを通るので、
4=-1/6・4+q
q=4+2/3
=14/3
になり、求める直線の式は、
y=-1/6・x+14/3
で、これが答えです。
次の[問1]の(2)です。
点AとBのx座標はそれぞれtとt-6で、これらの点はy=1/4・x^2上にあるので、それらのy座標はそれぞれ1/4・t^2、1/4・(t-6)^2です。
つまり、点AとBの座標は、それぞれ、
点A(t,1/4・t^2)
点B(t-6,1/4・(t-6)^2)
です。
次に点Cの座標を求めます。
与えられた条件から、四角形OABCは平行四辺形なので、
OA=BC
OA//BC
が成り立ち、OAのx変化量がBCのx変化量に等しいので、点Cのx座標は2t-6で、また、点Cはy=5/4・x^2上にあるので、そのy座標は、5/4・(2t-6)^2です。
つまり、点Cの座標は、
点C(2t-6,5/4・(2t-6)^2)
です。
ここで、点A、点B、点Cの座標を図5に書き入れましょう。

▲図5.点A、点B、点Cの座標を書き入れました
あとは、これらの座標から四角形OABCが平行四辺形になる条件を立式すればOKです。
そこで、点Cのx座標を求めるときOA=BCを使ったので、OA//OB、つまり、直線OAと直線BCの傾きが等しくなる条件を立式するのが簡単でしょう。(最後に記したように、平行四辺形になるための5つの条件のどれを使ってもOKです)
そこで、それぞれの直線の傾きを求めて等式をつくると、
 [1]
[1]になります。
そして、これを整理して因数分解すると、
 [2]
[2]です。
[2]から、t=2または4ですが、それぞれの場合の点Cのx座標を計算すると、
t=2のとき、2×2-6=-2
t=4のとき、2×4-6=2
となり、点Cのx座標が負の数であることから、t=2で、これが答えです。
続いて[問2]です。
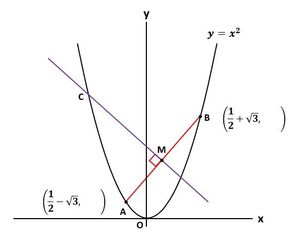
まず、与えられた条件で、点A、点B、点Cの座標を計算し、図6に書き入れましょう。

▲図6.点A、点B、点Cの座標を書き入れました
このとき、直線OCの式は、
 [3]
[3]です。
また図6に示すように、点Aと点Bを結んだ直線と、点Oと点Cを結んだ直線との交点をM、点Aから直線OCに下ろした垂線の足をN、点Bから直線OCに下ろした垂線の足をLとします。
すると、△OACの面積S(A)と△OCBの面積S(B)は、それぞれ、
S(A)=OC×AN×1/2
S(B)=OC×BL×1/2
になり、その面積比は、
S(A):S(B)=OC×AN×1/2:OC×BL×1/2
=AN:BL
です。
また、与えられた条件からこの面積比が2:1になので、
AN:BL=2:1
になります。
一方、△ANM∽△BLMから、
AN:BL=AM:BM
なので、
AM:BM=2:1
です。
ここで、点Aと点Bのy座標はどちらも9/4で、点Mは直線AB上にあるので、点Mのy座標は9/4です。
さらに、線分ABの長さは6で、点Mは線分ABを2:1に内分するので、点Mのx座標は-1です。
つまり、点Mの座標は(-1,9/4)になります。
そして、点Mは直線OC上にあるので、[3]に(-1,9/4)を代入すると、
9/4=-3/2・a・(-1)
a=3/2
で、これが答えです。
[問1]の(2)は、平行四辺形になるための5つの条件
・2組の対辺がそれぞれ平行
・2組の対辺がそれぞれ等しい
・2組の対角がそれぞれ等しい
・対角線がそれぞれの中点で交わる
・1組の対辺が平行で長さが等しい
のどれを使ってもOKです。(ここでは、最後の「1組の対辺が平行で長さが等しい」を使いました)
また、[問2]は、点(x1,y1)から直線ax+by+c=0に下ろした垂線の長さがlax1+by1+cl/√(a^2+b^2)になることを利用する方法もあります。
興味のある人は調べてみてください。




















 」
」

 (1)
(1) (2)
(2) (3)
(3)



 」
」





 」
」
 [1]
[1]



 [2]
[2]
 [3]
[3]
 [4]
[4]














 <1>
<1>