こんにちは。東久留米市の学習塾塾長です。
関東地方も梅雨明けになりました。しかし、天気図には夏の太平洋高気圧が見当たらず、その代わりにオホーツク海高気圧が元気なので、しばらく猛暑にはならないようです。
さて、今回は2013年ジュニア数学オリンピック予選に出題された場合の数の問題を取り上げます。
問題は、
「下図のように10個の点が並んでおり、このうち相異なる5個の点に印がついている。10個の点のうち4個を通るような直線は5本あり、下図において実線で示されている。このうちどの直線についても、直線上にある4点のうち、印がついているものはちょうど2個であった。このような印のつき方は全部で何通りあるか。ただし、回転や裏返しで一致するものも区別して数える。」
です。
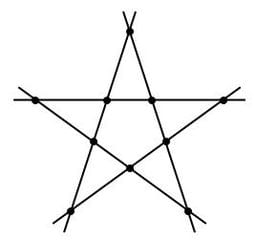
▲問題図
早速、取り掛かりましょう。
例えば図1のように、問題図の星形の外側の5点に印がついた場合、5本のすべての直線について、それらの上の4点のうち2点に印がついているので、これは条件を満たしています。(印を●、4点中2点に印がついた直線を青色線で示しました)
つまり、条件を満たす印のつき方は1通りです。

▲図1.星形の外側の5点に印がついた場合
一方、図2のように、星形の内側の5個の点に印がついた場合、これも条件を満たし、印のつき方は1通りです。

▲図2.星形の内側の5点に印がついた場合
そうすると、あとは星形の外側の5点のなかに、(1)印が4点の場合、(2)印が3点の場合、(3)印が2点の場合、(4)印が1点の場合、の4通りを調べれば良さそうです。
(1)印が4点の場合
図3のように、内側の5点のどこに印をつけても、4点中3点に印がついた直線ができるので、この場合は条件を満たしません。
したgって、印のつき方は0通りです。

▲図3.外側の4点に印がついた場合
(2)印が3点の場合
外側の3点の印のつけ方は、(2-1)3点が互いに隣り合う場合と(2-2)2点が隣り合い、1点が離れている場合に分けられます。
(2-1)3点が互いに隣り合う場合
図4のように、内側に2点に印(●)をつけることにより、条件を満たします。
このとき、外側の5点から3点が互いに隣り合う選び方は5通りなので、条件を満たす印のつき方は5通りです。
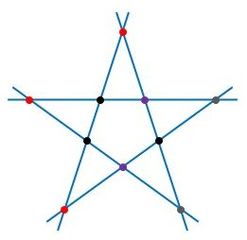
▲図4.3点が互いに隣り合う場合
(2-2)2点が隣り合い、1点が離れている場合
図5のように、条件を満たすことはできないので、印のつき方は0通りです。
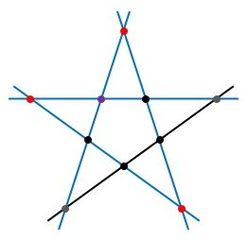
▲図5.2点が隣り合い、1点が離れている場合
(3)印が2点の場合
外側の2点の印の付け方は、(3-1)2点が隣り合う場合と(3-2)2点が離れている場合に分けられます。
(3-1)2点が隣り合う場合
図6のように、内側に3点記しをつけることにより、条件を満たします。
このとき、外側の5点から2点が隣り合う選び方は5通りなので、条件を満たす印のつき方は5通りです。
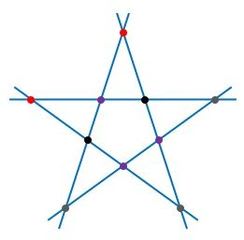
▲図6.2点が隣り合う場合
(3-2)2点が離れている場合
図7のように、条件を満たすことができないので、印のつき方は0通りです。

▲図7.2点が離れている場合
(4)印が1点の場合
図8のように、条件をみたすことができないので、印のつき方は0通りです。
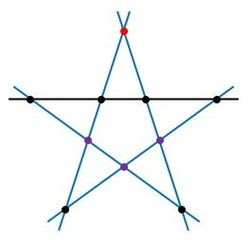
▲図8.印が1点の場合
以上をまとめると、条件を満たす印のつき方の合計は、1+1+5+5=12通りで、これが答えです。
図を描いて調べれば簡単な問題です。
関東地方も梅雨明けになりました。しかし、天気図には夏の太平洋高気圧が見当たらず、その代わりにオホーツク海高気圧が元気なので、しばらく猛暑にはならないようです。
さて、今回は2013年ジュニア数学オリンピック予選に出題された場合の数の問題を取り上げます。
問題は、
「下図のように10個の点が並んでおり、このうち相異なる5個の点に印がついている。10個の点のうち4個を通るような直線は5本あり、下図において実線で示されている。このうちどの直線についても、直線上にある4点のうち、印がついているものはちょうど2個であった。このような印のつき方は全部で何通りあるか。ただし、回転や裏返しで一致するものも区別して数える。」
です。

▲問題図
早速、取り掛かりましょう。
例えば図1のように、問題図の星形の外側の5点に印がついた場合、5本のすべての直線について、それらの上の4点のうち2点に印がついているので、これは条件を満たしています。(印を●、4点中2点に印がついた直線を青色線で示しました)
つまり、条件を満たす印のつき方は1通りです。

▲図1.星形の外側の5点に印がついた場合
一方、図2のように、星形の内側の5個の点に印がついた場合、これも条件を満たし、印のつき方は1通りです。

▲図2.星形の内側の5点に印がついた場合
そうすると、あとは星形の外側の5点のなかに、(1)印が4点の場合、(2)印が3点の場合、(3)印が2点の場合、(4)印が1点の場合、の4通りを調べれば良さそうです。
(1)印が4点の場合
図3のように、内側の5点のどこに印をつけても、4点中3点に印がついた直線ができるので、この場合は条件を満たしません。
したgって、印のつき方は0通りです。

▲図3.外側の4点に印がついた場合
(2)印が3点の場合
外側の3点の印のつけ方は、(2-1)3点が互いに隣り合う場合と(2-2)2点が隣り合い、1点が離れている場合に分けられます。
(2-1)3点が互いに隣り合う場合
図4のように、内側に2点に印(●)をつけることにより、条件を満たします。
このとき、外側の5点から3点が互いに隣り合う選び方は5通りなので、条件を満たす印のつき方は5通りです。

▲図4.3点が互いに隣り合う場合
(2-2)2点が隣り合い、1点が離れている場合
図5のように、条件を満たすことはできないので、印のつき方は0通りです。

▲図5.2点が隣り合い、1点が離れている場合
(3)印が2点の場合
外側の2点の印の付け方は、(3-1)2点が隣り合う場合と(3-2)2点が離れている場合に分けられます。
(3-1)2点が隣り合う場合
図6のように、内側に3点記しをつけることにより、条件を満たします。
このとき、外側の5点から2点が隣り合う選び方は5通りなので、条件を満たす印のつき方は5通りです。

▲図6.2点が隣り合う場合
(3-2)2点が離れている場合
図7のように、条件を満たすことができないので、印のつき方は0通りです。

▲図7.2点が離れている場合
(4)印が1点の場合
図8のように、条件をみたすことができないので、印のつき方は0通りです。

▲図8.印が1点の場合
以上をまとめると、条件を満たす印のつき方の合計は、1+1+5+5=12通りで、これが答えです。
図を描いて調べれば簡単な問題です。










