こんにちは。東久留米市の学習塾塾長です。
昨日より寒くなったので、少し厚手のセーターを着てきました。明日は気温が少し上がるようですが、もう11月なので段々寒くなっていきます。受験生の皆さんは、体調に気をつけて、入試の準備を進めてください。
さて、今回は都立御三家の確率問題です。
問題は平成23年度日比谷で出題されたもので、それは、
「1から6までの目の出る大小1つずつのさいころを同時に投げる。
大きいさいころの出た目の数をa、小さいさいころの出た目の数をbとし、aとbの積をcとするとき、√(216/c)の値が整数になる確率を求めよ。
ただし、大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。」
です。
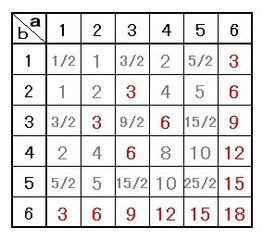
まず、1から6までのa、bについて、それぞれ√(216/c)を計算して表を作りましょう。その結果が下表です。
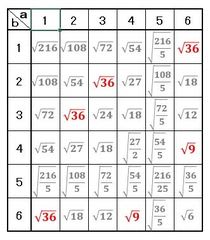
▲表.1から6までのa、bに対応する√(216/c)の値
この表から、すべての場合の数は36通り、√(216/c)が整数になる場合の数は6通りと判るので、√(216/c)が整数になる確率は、6/36=1/6で、これが答えです。
次に、表を利用しない解き方を調べましょう。
216を素因数分解すると、216=2^3×3^3 です。
√(216/c)が整数になるためには、216/cが平方数にならなくてはなりません。したがって、cは因数として、2を1つまたは3つ、かつ、3を1つまたは3つ持たなければなりません。
つまり、可能なcは、2×3=6、2^3×3=24、2×3^3=54、2^3×3^3=216になります。
ところが、c=abで、1≦a、b≦6 (a、bは整数)なので、1≦c≦36ですから、結局cの取り得る値は、6または24となります。
そこで、c=6となるa、bの組合せ(a,b)を調べると、それは、(1,6)(2,3)(3,2)(6,1)の4通りです。
さらに、c=24となるものは、(4,6)(6,4)の2通りで、c=6と24の場合を合わせると6通りになります。
すべての場合の数は36通りなので、求める確率は、6/36=1/6になります。
この問題のように根号を持つ数が整数になるというような場合、根号のなかの数を素因数分解するのが定石です。しっかり覚えておきましょう。
昨日より寒くなったので、少し厚手のセーターを着てきました。明日は気温が少し上がるようですが、もう11月なので段々寒くなっていきます。受験生の皆さんは、体調に気をつけて、入試の準備を進めてください。
さて、今回は都立御三家の確率問題です。
問題は平成23年度日比谷で出題されたもので、それは、
「1から6までの目の出る大小1つずつのさいころを同時に投げる。
大きいさいころの出た目の数をa、小さいさいころの出た目の数をbとし、aとbの積をcとするとき、√(216/c)の値が整数になる確率を求めよ。
ただし、大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。」
です。
まず、1から6までのa、bについて、それぞれ√(216/c)を計算して表を作りましょう。その結果が下表です。

▲表.1から6までのa、bに対応する√(216/c)の値
この表から、すべての場合の数は36通り、√(216/c)が整数になる場合の数は6通りと判るので、√(216/c)が整数になる確率は、6/36=1/6で、これが答えです。
次に、表を利用しない解き方を調べましょう。
216を素因数分解すると、216=2^3×3^3 です。
√(216/c)が整数になるためには、216/cが平方数にならなくてはなりません。したがって、cは因数として、2を1つまたは3つ、かつ、3を1つまたは3つ持たなければなりません。
つまり、可能なcは、2×3=6、2^3×3=24、2×3^3=54、2^3×3^3=216になります。
ところが、c=abで、1≦a、b≦6 (a、bは整数)なので、1≦c≦36ですから、結局cの取り得る値は、6または24となります。
そこで、c=6となるa、bの組合せ(a,b)を調べると、それは、(1,6)(2,3)(3,2)(6,1)の4通りです。
さらに、c=24となるものは、(4,6)(6,4)の2通りで、c=6と24の場合を合わせると6通りになります。
すべての場合の数は36通りなので、求める確率は、6/36=1/6になります。
この問題のように根号を持つ数が整数になるというような場合、根号のなかの数を素因数分解するのが定石です。しっかり覚えておきましょう。