こんにちは。東久留米市の学習塾塾長です。
東久留米の気温は25℃と過ごしやすい日になりました。しかし明日から気温が上がり、土曜日は30℃、日曜日には32℃に達する予報です。その対策の一環で、朝、スーパーマーケットでビール(正しくは発泡酒)を買いました。冷蔵庫で冷やして、週末に飲む予定です。
さて、今回は2010年日本数学オリンピック本選に出題された図形問題を取り上げます。
問題は、
「AB≠ACなる鋭角三角形ABCがあり、AからBCにおろした垂線の足をHとおく。点P、Qを、3点A、B、Pと3点A、C、Qがともにこの順に一直線上に並ぶようにとると、4点B、C、P、Qは同一円周上にあり、HP=HQが成り立った。このときHは三角形APQの外心であることを示せ。ただし、XYで線分XYの長さを表すものとする。」
です。
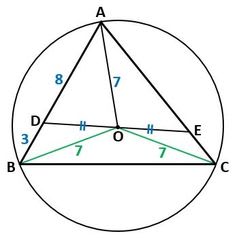
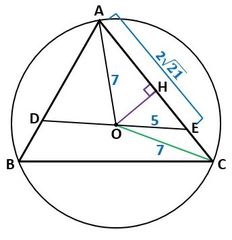
早速、図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
まず、図1から簡単に得られる情報について調べてみましょう。
仮定からB、P、Q、Cが同一円周上にあるので、
∠CQP+∠CBP=180°
∠CQP=180°-∠CBP (1)
です。
一方、仮定からA、B、Pは一直線上にあるので、
∠ABC+∠CBP=180°
∠ABC=180°-∠CBP (2)
です。
したがって、(1)(2)から、図2のように、
∠ABC=∠CQP=∠AQP (3)
が成り立ちます。(∠ACB=∠APQも同じです)

▲図2.∠ABC=∠AQP(∠ACB=∠APQ)です
それでは問題に取り掛かりましょう。
Hが△APQの外心であることを示すためには、HA=HP(HQ)←△HAP(△HAQ)が二等辺三角形←∠HAP=∠HPA(∠HQA)を示せばOKですが、これより、新たに点Rをおいて、四角形APQRが同一円周上にあることを示す方法(よく使う方法です)のほうが簡単そうです。
このとき図3のように、RはAHを対称軸としてPと対応する点がよいでしょう。

▲図3.対称軸をAHとしてPの対応する点をRにしました
初めに、PとRを直線で結ぶと直線PRは直線AHと直交し、∠AHB=∠AMPなので、
BC//PR
です。
そして、平行線の同位角は等しいので、
∠ABC=∠APR (4)
です。
一方、△APRは二等辺三角形なので、
∠APR=∠ARP (5)
です。
すると(3)(4)(5)から
∠AQP=∠ARP
が成り立ち、円周角の定理の逆から、A、P、Q、Rは同一円周上にあることが判りました。
ところが、HP=HQ=HRから、P、Q、Rは中心をHとする円周上にあるので、A、P、Q、Rも同じ円周上にあることになります。
したがって、Hは△APQの外心です。
対称の点をおくテクニックは、以前にも取り上げています。(例えばジュニア数学オリンピックの難しい問題(4)) 頭にいれておくと役に立つかもしれません。
東久留米の気温は25℃と過ごしやすい日になりました。しかし明日から気温が上がり、土曜日は30℃、日曜日には32℃に達する予報です。その対策の一環で、朝、スーパーマーケットでビール(正しくは発泡酒)を買いました。冷蔵庫で冷やして、週末に飲む予定です。
さて、今回は2010年日本数学オリンピック本選に出題された図形問題を取り上げます。
問題は、
「AB≠ACなる鋭角三角形ABCがあり、AからBCにおろした垂線の足をHとおく。点P、Qを、3点A、B、Pと3点A、C、Qがともにこの順に一直線上に並ぶようにとると、4点B、C、P、Qは同一円周上にあり、HP=HQが成り立った。このときHは三角形APQの外心であることを示せ。ただし、XYで線分XYの長さを表すものとする。」
です。
早速、図1のように、問題の図を描きましょう。

▲図1.問題の図を描きました
まず、図1から簡単に得られる情報について調べてみましょう。
仮定からB、P、Q、Cが同一円周上にあるので、
∠CQP+∠CBP=180°
∠CQP=180°-∠CBP (1)
です。
一方、仮定からA、B、Pは一直線上にあるので、
∠ABC+∠CBP=180°
∠ABC=180°-∠CBP (2)
です。
したがって、(1)(2)から、図2のように、
∠ABC=∠CQP=∠AQP (3)
が成り立ちます。(∠ACB=∠APQも同じです)

▲図2.∠ABC=∠AQP(∠ACB=∠APQ)です
それでは問題に取り掛かりましょう。
Hが△APQの外心であることを示すためには、HA=HP(HQ)←△HAP(△HAQ)が二等辺三角形←∠HAP=∠HPA(∠HQA)を示せばOKですが、これより、新たに点Rをおいて、四角形APQRが同一円周上にあることを示す方法(よく使う方法です)のほうが簡単そうです。
このとき図3のように、RはAHを対称軸としてPと対応する点がよいでしょう。

▲図3.対称軸をAHとしてPの対応する点をRにしました
初めに、PとRを直線で結ぶと直線PRは直線AHと直交し、∠AHB=∠AMPなので、
BC//PR
です。
そして、平行線の同位角は等しいので、
∠ABC=∠APR (4)
です。
一方、△APRは二等辺三角形なので、
∠APR=∠ARP (5)
です。
すると(3)(4)(5)から
∠AQP=∠ARP
が成り立ち、円周角の定理の逆から、A、P、Q、Rは同一円周上にあることが判りました。
ところが、HP=HQ=HRから、P、Q、Rは中心をHとする円周上にあるので、A、P、Q、Rも同じ円周上にあることになります。
したがって、Hは△APQの外心です。
対称の点をおくテクニックは、以前にも取り上げています。(例えばジュニア数学オリンピックの難しい問題(4)) 頭にいれておくと役に立つかもしれません。